Generalized Likelihood Ratio Test for Adversarially Robust Hypothesis Testing
Paper and Code
Dec 04, 2021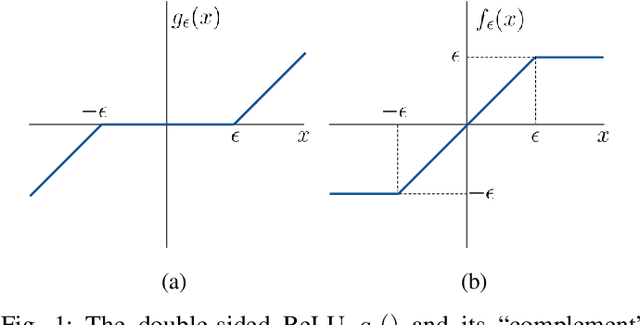
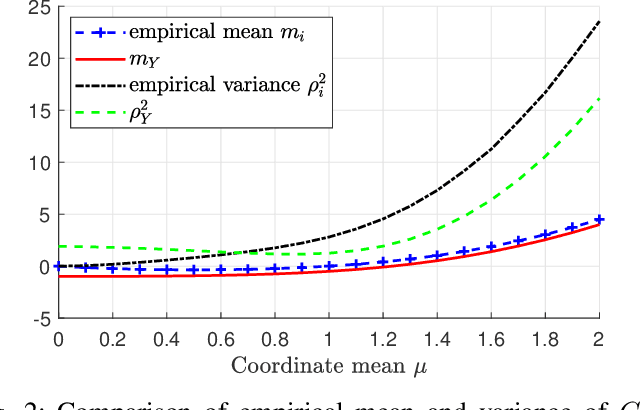
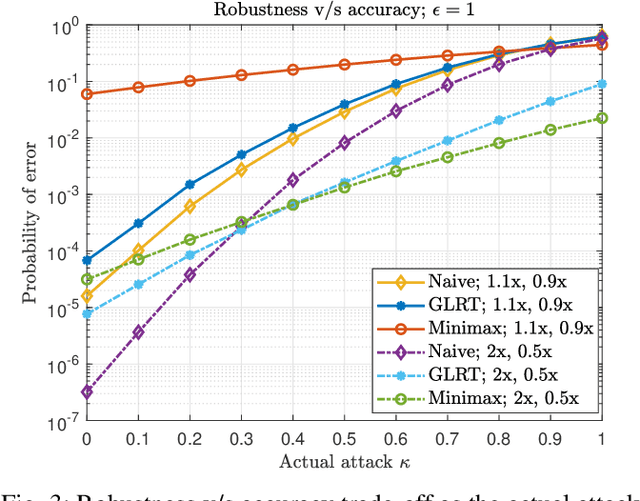
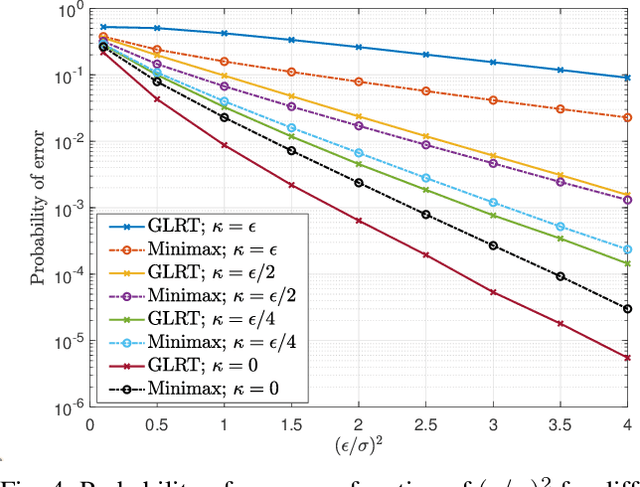
Machine learning models are known to be susceptible to adversarial attacks which can cause misclassification by introducing small but well designed perturbations. In this paper, we consider a classical hypothesis testing problem in order to develop fundamental insight into defending against such adversarial perturbations. We interpret an adversarial perturbation as a nuisance parameter, and propose a defense based on applying the generalized likelihood ratio test (GLRT) to the resulting composite hypothesis testing problem, jointly estimating the class of interest and the adversarial perturbation. While the GLRT approach is applicable to general multi-class hypothesis testing, we first evaluate it for binary hypothesis testing in white Gaussian noise under $\ell_{\infty}$ norm-bounded adversarial perturbations, for which a known minimax defense optimizing for the worst-case attack provides a benchmark. We derive the worst-case attack for the GLRT defense, and show that its asymptotic performance (as the dimension of the data increases) approaches that of the minimax defense. For non-asymptotic regimes, we show via simulations that the GLRT defense is competitive with the minimax approach under the worst-case attack, while yielding a better robustness-accuracy tradeoff under weaker attacks. We also illustrate the GLRT approach for a multi-class hypothesis testing problem, for which a minimax strategy is not known, evaluating its performance under both noise-agnostic and noise-aware adversarial settings, by providing a method to find optimal noise-aware attacks, and heuristics to find noise-agnostic attacks that are close to optimal in the high SNR regime.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge