Adaptive Sparse Möbius Transforms for Learning Polynomials

We consider the problem of exactly learning an $s$-sparse real-valued Boolean polynomial of degree $d$ of the form $f:\{ 0,1\}^n \rightarrow \mathbb{R}$. This problem corresponds to decomposing functions in the AND basis and is known as taking a Möbius transform. While the analogous problem for the parity basis (Fourier transform) $f: \{-1,1 \}^n \rightarrow \mathbb{R}$ is well-understood, the AND basis presents a unique challenge: the basis vectors are coherent, precluding standard compressed sensing methods. We overcome this challenge by identifying that we can exploit adaptive group testing to provide a constructive, query-efficient implementation of the Möbius transform (also known as Möbius inversion) for sparse functions. We present two algorithms based on this insight. The Fully-Adaptive Sparse Möbius Transform (FASMT) uses $O(sd \log(n/d))$ adaptive queries in $O((sd + n) sd \log(n/d))$ time, which we show is near-optimal in query complexity. Furthermore, we also present the Partially-Adaptive Sparse Möbius Transform (PASMT), which uses $O(sd^2\log(n/d))$ queries, trading a factor of $d$ to reduce the number of adaptive rounds to $O(d^2\log(n/d))$, with no dependence on $s$. When applied to hypergraph reconstruction from edge-count queries, our results improve upon baselines by avoiding the combinatorial explosion in the rank $d$. We demonstrate the practical utility of our method for hypergraph reconstruction by applying it to learning real hypergraphs in simulations.

ProxySPEX: Inference-Efficient Interpretability via Sparse Feature Interactions in LLMs

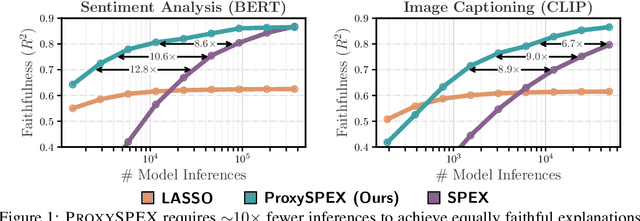
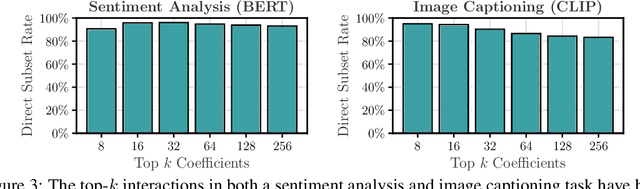
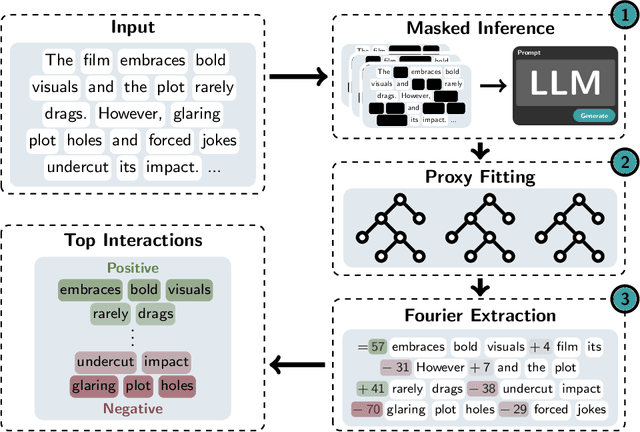
Large Language Models (LLMs) have achieved remarkable performance by capturing complex interactions between input features. To identify these interactions, most existing approaches require enumerating all possible combinations of features up to a given order, causing them to scale poorly with the number of inputs $n$. Recently, Kang et al. (2025) proposed SPEX, an information-theoretic approach that uses interaction sparsity to scale to $n \approx 10^3$ features. SPEX greatly improves upon prior methods but requires tens of thousands of model inferences, which can be prohibitive for large models. In this paper, we observe that LLM feature interactions are often hierarchical -- higher-order interactions are accompanied by their lower-order subsets -- which enables more efficient discovery. To exploit this hierarchy, we propose ProxySPEX, an interaction attribution algorithm that first fits gradient boosted trees to masked LLM outputs and then extracts the important interactions. Experiments across four challenging high-dimensional datasets show that ProxySPEX more faithfully reconstructs LLM outputs by 20% over marginal attribution approaches while using $10\times$ fewer inferences than SPEX. By accounting for interactions, ProxySPEX identifies features that influence model output over 20% more than those selected by marginal approaches. Further, we apply ProxySPEX to two interpretability tasks. Data attribution, where we identify interactions among CIFAR-10 training samples that influence test predictions, and mechanistic interpretability, where we uncover interactions between attention heads, both within and across layers, on a question-answering task. ProxySPEX identifies interactions that enable more aggressive pruning of heads than marginal approaches.

Online Assortment and Price Optimization Under Contextual Choice Models

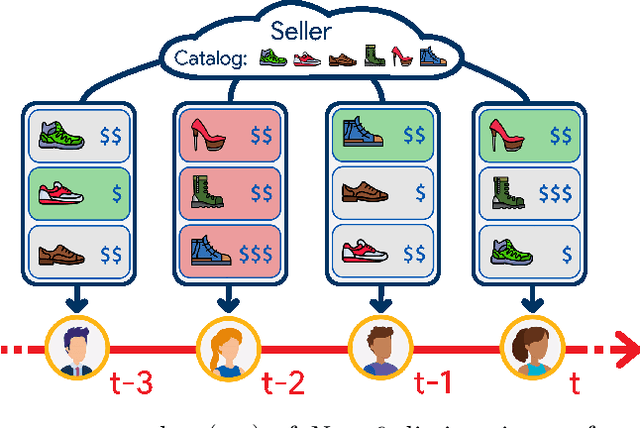
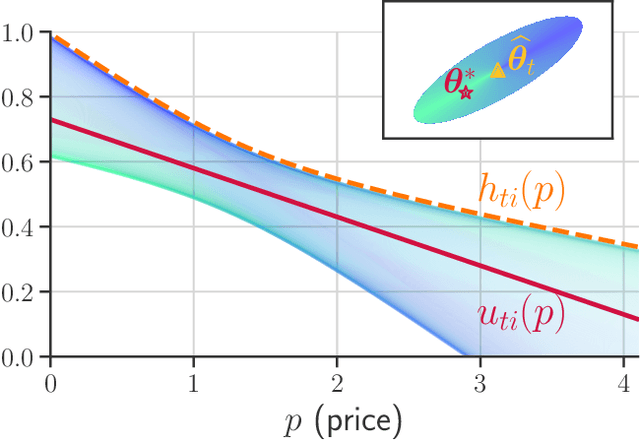
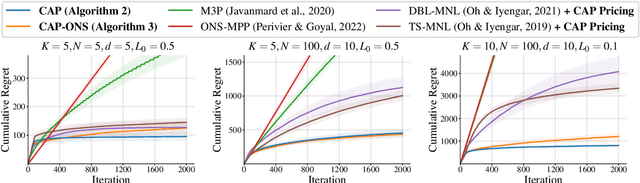
We consider an assortment selection and pricing problem in which a seller has $N$ different items available for sale. In each round, the seller observes a $d$-dimensional contextual preference information vector for the user, and offers to the user an assortment of $K$ items at prices chosen by the seller. The user selects at most one of the products from the offered assortment according to a multinomial logit choice model whose parameters are unknown. The seller observes which, if any, item is chosen at the end of each round, with the goal of maximizing cumulative revenue over a selling horizon of length $T$. For this problem, we propose an algorithm that learns from user feedback and achieves a revenue regret of order $\widetilde{O}(d \sqrt{K T} / L_0 )$ where $L_0$ is the minimum price sensitivity parameter. We also obtain a lower bound of order $\Omega(d \sqrt{T}/ L_0)$ for the regret achievable by any algorithm.

SPEX: Scaling Feature Interaction Explanations for LLMs

Large language models (LLMs) have revolutionized machine learning due to their ability to capture complex interactions between input features. Popular post-hoc explanation methods like SHAP provide marginal feature attributions, while their extensions to interaction importances only scale to small input lengths ($\approx 20$). We propose Spectral Explainer (SPEX), a model-agnostic interaction attribution algorithm that efficiently scales to large input lengths ($\approx 1000)$. SPEX exploits underlying natural sparsity among interactions -- common in real-world data -- and applies a sparse Fourier transform using a channel decoding algorithm to efficiently identify important interactions. We perform experiments across three difficult long-context datasets that require LLMs to utilize interactions between inputs to complete the task. For large inputs, SPEX outperforms marginal attribution methods by up to 20% in terms of faithfully reconstructing LLM outputs. Further, SPEX successfully identifies key features and interactions that strongly influence model output. For one of our datasets, HotpotQA, SPEX provides interactions that align with human annotations. Finally, we use our model-agnostic approach to generate explanations to demonstrate abstract reasoning in closed-source LLMs (GPT-4o mini) and compositional reasoning in vision-language models.

Efficiently Computing Sparse Fourier Transforms of $q$-ary Functions

Fourier transformations of pseudo-Boolean functions are popular tools for analyzing functions of binary sequences. Real-world functions often have structures that manifest in a sparse Fourier transform, and previous works have shown that under the assumption of sparsity the transform can be computed efficiently. But what if we want to compute the Fourier transform of functions defined over a $q$-ary alphabet? These types of functions arise naturally in many areas including biology. A typical workaround is to encode the $q$-ary sequence in binary, however, this approach is computationally inefficient and fundamentally incompatible with the existing sparse Fourier transform techniques. Herein, we develop a sparse Fourier transform algorithm specifically for $q$-ary functions of length $n$ sequences, dubbed $q$-SFT, which provably computes an $S$-sparse transform with vanishing error as $q^n \rightarrow \infty$ in $O(Sn)$ function evaluations and $O(S n^2 \log q)$ computations, where $S = q^{n\delta}$ for some $\delta < 1$. Under certain assumptions, we show that for fixed $q$, a robust version of $q$-SFT has a sample complexity of $O(Sn^2)$ and a computational complexity of $O(Sn^3)$ with the same asymptotic guarantees. We present numerical simulations on synthetic and real-world RNA data, demonstrating the scalability of $q$-SFT to massively high dimensional $q$-ary functions.

Interactive Learning with Pricing for Optimal and Stable Allocations in Markets

Large-scale online recommendation systems must facilitate the allocation of a limited number of items among competing users while learning their preferences from user feedback. As a principled way of incorporating market constraints and user incentives in the design, we consider our objectives to be two-fold: maximal social welfare with minimal instability. To maximize social welfare, our proposed framework enhances the quality of recommendations by exploring allocations that optimistically maximize the rewards. To minimize instability, a measure of users' incentives to deviate from recommended allocations, the algorithm prices the items based on a scheme derived from the Walrasian equilibria. Though it is known that these equilibria yield stable prices for markets with known user preferences, our approach accounts for the inherent uncertainty in the preferences and further ensures that the users accept their recommendations under offered prices. To the best of our knowledge, our approach is the first to integrate techniques from combinatorial bandits, optimal resource allocation, and collaborative filtering to obtain an algorithm that achieves sub-linear social welfare regret as well as sub-linear instability. Empirical studies on synthetic and real-world data also demonstrate the efficacy of our strategy compared to approaches that do not fully incorporate all these aspects.

Interactive Recommendations for Optimal Allocations in Markets with Constraints

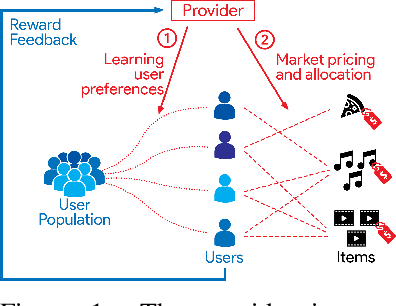
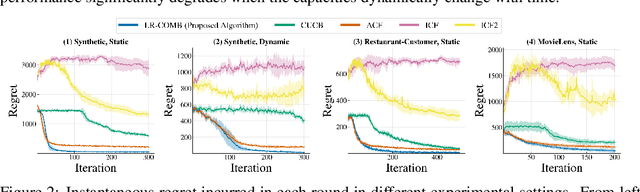
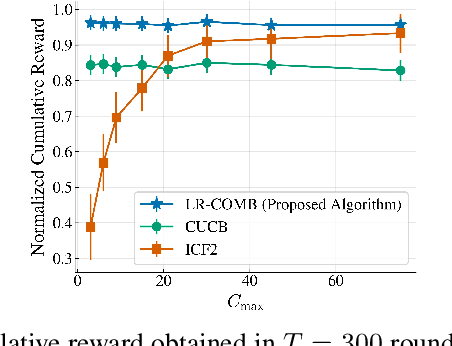
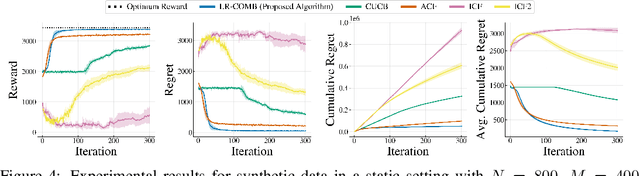
Recommendation systems when employed in markets play a dual role: they assist users in selecting their most desired items from a large pool and they help in allocating a limited number of items to the users who desire them the most. Despite the prevalence of capacity constraints on allocations in many real-world recommendation settings, a principled way of incorporating them in the design of these systems has been lacking. Motivated by this, we propose an interactive framework where the system provider can enhance the quality of recommendations to the users by opportunistically exploring allocations that maximize user rewards and respect the capacity constraints using appropriate pricing mechanisms. We model the problem as an instance of a low-rank combinatorial multi-armed bandit problem with selection constraints on the arms. We employ an integrated approach using techniques from collaborative filtering, combinatorial bandits, and optimal resource allocation to provide an algorithm that provably achieves sub-linear regret, namely $\tilde{\mathcal{O}} ( \sqrt{N M (N+M) RT} )$ in $T$ rounds for a problem with $N$ users, $M$ items and rank $R$ mean reward matrix. Empirical studies on synthetic and real-world data also demonstrate the effectiveness and performance of our approach.