Interactive Recommendations for Optimal Allocations in Markets with Constraints
Paper and Code
Jul 08, 2022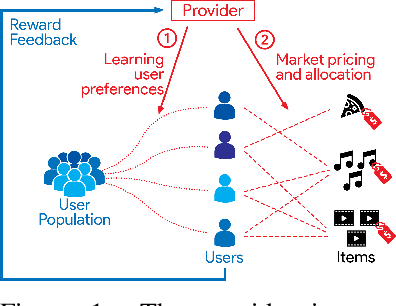
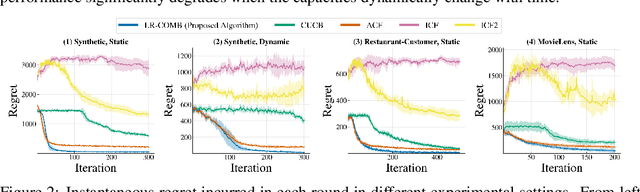
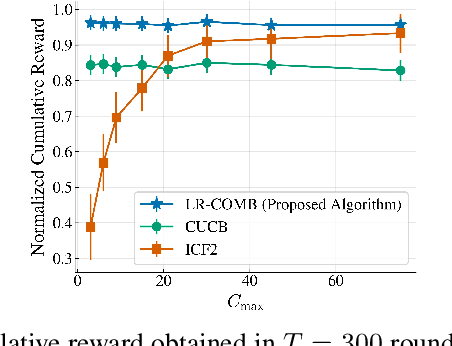
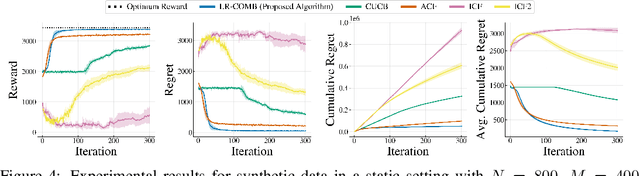
Recommendation systems when employed in markets play a dual role: they assist users in selecting their most desired items from a large pool and they help in allocating a limited number of items to the users who desire them the most. Despite the prevalence of capacity constraints on allocations in many real-world recommendation settings, a principled way of incorporating them in the design of these systems has been lacking. Motivated by this, we propose an interactive framework where the system provider can enhance the quality of recommendations to the users by opportunistically exploring allocations that maximize user rewards and respect the capacity constraints using appropriate pricing mechanisms. We model the problem as an instance of a low-rank combinatorial multi-armed bandit problem with selection constraints on the arms. We employ an integrated approach using techniques from collaborative filtering, combinatorial bandits, and optimal resource allocation to provide an algorithm that provably achieves sub-linear regret, namely $\tilde{\mathcal{O}} ( \sqrt{N M (N+M) RT} )$ in $T$ rounds for a problem with $N$ users, $M$ items and rank $R$ mean reward matrix. Empirical studies on synthetic and real-world data also demonstrate the effectiveness and performance of our approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge