Amirali Aghazadeh
cryoSENSE: Compressive Sensing Enables High-throughput Microscopy with Sparse and Generative Priors on the Protein Cryo-EM Image Manifold
Nov 18, 2025
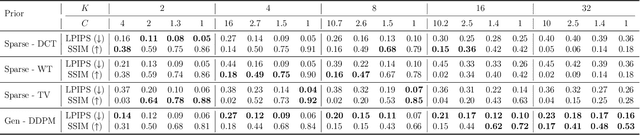
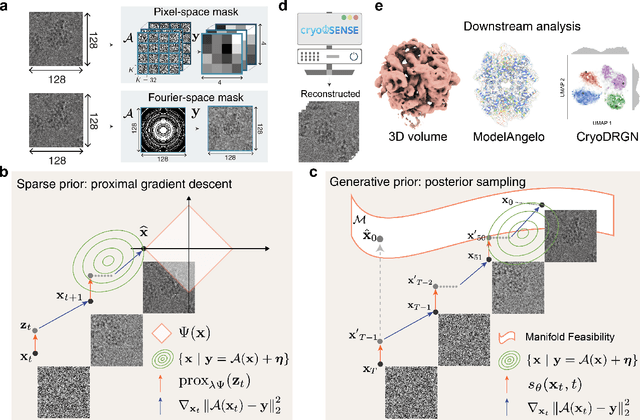
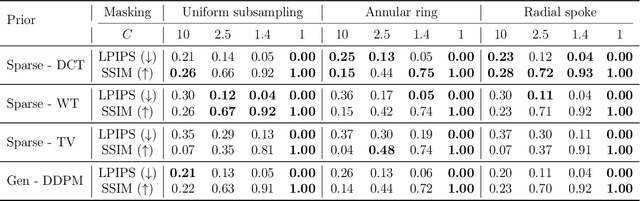
Abstract:Cryo-electron microscopy (cryo-EM) enables the atomic-resolution visualization of biomolecules; however, modern direct detectors generate data volumes that far exceed the available storage and transfer bandwidth, thereby constraining practical throughput. We introduce cryoSENSE, the computational realization of a hardware-software co-designed framework for compressive cryo-EM sensing and acquisition. We show that cryo-EM images of proteins lie on low-dimensional manifolds that can be independently represented using sparse priors in predefined bases and generative priors captured by a denoising diffusion model. cryoSENSE leverages these low-dimensional manifolds to enable faithful image reconstruction from spatial and Fourier-domain undersampled measurements while preserving downstream structural resolution. In experiments, cryoSENSE increases acquisition throughput by up to 2.5$\times$ while retaining the original 3D resolution, offering controllable trade-offs between the number of masked measurements and the level of downsampling. Sparse priors favor faithful reconstruction from Fourier-domain measurements and moderate compression, whereas generative diffusion priors achieve accurate recovery from pixel-domain measurements and more severe undersampling. Project website: https://cryosense.github.io.
AstroAgents: A Multi-Agent AI for Hypothesis Generation from Mass Spectrometry Data
Mar 29, 2025Abstract:With upcoming sample return missions across the solar system and the increasing availability of mass spectrometry data, there is an urgent need for methods that analyze such data within the context of existing astrobiology literature and generate plausible hypotheses regarding the emergence of life on Earth. Hypothesis generation from mass spectrometry data is challenging due to factors such as environmental contaminants, the complexity of spectral peaks, and difficulties in cross-matching these peaks with prior studies. To address these challenges, we introduce AstroAgents, a large language model-based, multi-agent AI system for hypothesis generation from mass spectrometry data. AstroAgents is structured around eight collaborative agents: a data analyst, a planner, three domain scientists, an accumulator, a literature reviewer, and a critic. The system processes mass spectrometry data alongside user-provided research papers. The data analyst interprets the data, and the planner delegates specific segments to the scientist agents for in-depth exploration. The accumulator then collects and deduplicates the generated hypotheses, and the literature reviewer identifies relevant literature using Semantic Scholar. The critic evaluates the hypotheses, offering rigorous suggestions for improvement. To assess AstroAgents, an astrobiology expert evaluated the novelty and plausibility of more than a hundred hypotheses generated from data obtained from eight meteorites and ten soil samples. Of these hypotheses, 36% were identified as plausible, and among those, 66% were novel. Project website: https://astroagents.github.io/
Efficient Algorithm for Sparse Fourier Transform of Generalized q-ary Functions
Jan 21, 2025Abstract:Computing the Fourier transform of a $q$-ary function $f:\mathbb{Z}_{q}^n\rightarrow \mathbb{R}$, which maps $q$-ary sequences to real numbers, is an important problem in mathematics with wide-ranging applications in biology, signal processing, and machine learning. Previous studies have shown that, under the sparsity assumption, the Fourier transform can be computed efficiently using fast and sample-efficient algorithms. However, in many practical settings, the function is defined over a more general space -- the space of generalized $q$-ary sequences $\mathbb{Z}_{q_1} \times \mathbb{Z}_{q_2} \times \cdots \times \mathbb{Z}_{q_n}$ -- where each $\mathbb{Z}_{q_i}$ corresponds to integers modulo $q_i$. A naive approach involves setting $q=\max_i{q_i}$ and treating the function as $q$-ary, which results in heavy computational overheads. Herein, we develop GFast, an algorithm that computes the $S$-sparse Fourier transform of $f$ with a sample complexity of $O(Sn)$, computational complexity of $O(Sn \log N)$, and a failure probability that approaches zero as $N=\prod_{i=1}^n q_i \rightarrow \infty$ with $S = N^\delta$ for some $0 \leq \delta < 1$. In the presence of noise, we further demonstrate that a robust version of GFast computes the transform with a sample complexity of $O(Sn^2)$ and computational complexity of $O(Sn^2 \log N)$ under the same high probability guarantees. Using large-scale synthetic experiments, we demonstrate that GFast computes the sparse Fourier transform of generalized $q$-ary functions using $16\times$ fewer samples and running $8\times$ faster than existing algorithms. In real-world protein fitness datasets, GFast explains the predictive interactions of a neural network with $>25\%$ smaller normalized mean-squared error compared to existing algorithms.
SHAP zero Explains All-order Feature Interactions in Black-box Genomic Models with Near-zero Query Cost
Oct 25, 2024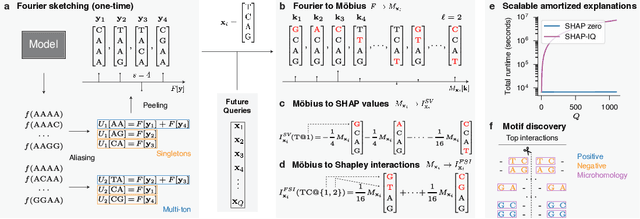
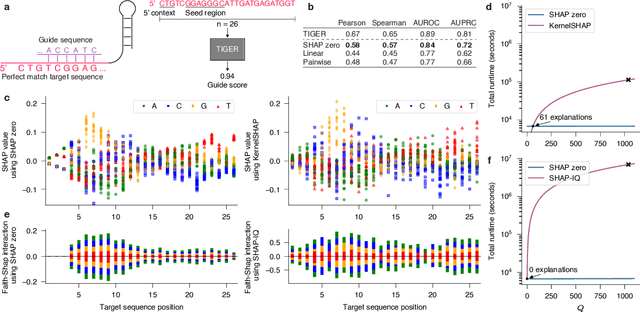
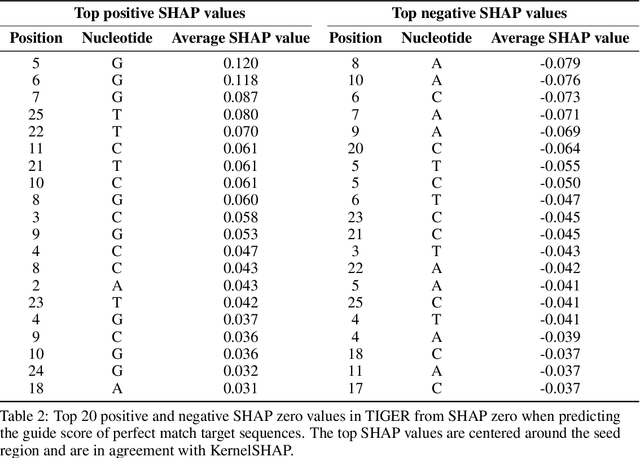
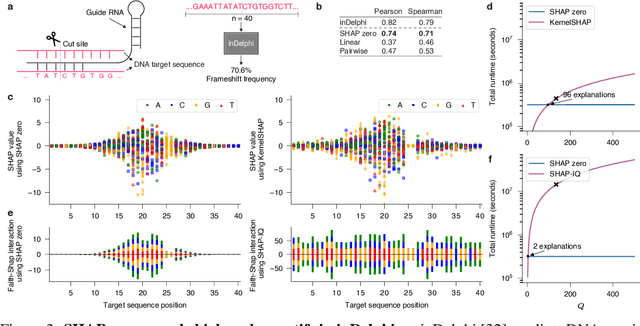
Abstract:With the rapid growth of black-box models in machine learning, Shapley values have emerged as a popular method for model explanations due to their theoretical guarantees. Shapley values locally explain a model to an input query using additive features. Yet, in genomics, extracting biological knowledge from black-box models hinges on explaining nonlinear feature interactions globally to hundreds to thousands of input query sequences. Herein, we develop SHAP zero, an algorithm that estimates all-order Shapley feature interactions with a near-zero cost per queried sequence after paying a one-time fee for model sketching. SHAP zero achieves this by establishing a surprisingly underexplored connection between the Shapley interactions and the Fourier transform of the model. Explaining two genomic models, one trained to predict guide RNA binding and the other to predict DNA repair outcomes, we demonstrate that SHAP zero achieves orders of magnitude reduction in amortized computational cost compared to state-of-the-art algorithms. SHAP zero reveals all microhomologous motifs that are predictive of DNA repair outcome, a finding previously inaccessible due to the combinatorial space of possible high-order feature interactions.
ProtiGeno: a prokaryotic short gene finder using protein language models
Jul 19, 2023Abstract:Prokaryotic gene prediction plays an important role in understanding the biology of organisms and their function with applications in medicine and biotechnology. Although the current gene finders are highly sensitive in finding long genes, their sensitivity decreases noticeably in finding shorter genes (<180 nts). The culprit is insufficient annotated gene data to identify distinguishing features in short open reading frames (ORFs). We develop a deep learning-based method called ProtiGeno, specifically targeting short prokaryotic genes using a protein language model trained on millions of evolved proteins. In systematic large-scale experiments on 4,288 prokaryotic genomes, we demonstrate that ProtiGeno predicts short coding and noncoding genes with higher accuracy and recall than the current state-of-the-art gene finders. We discuss the predictive features of ProtiGeno and possible limitations by visualizing the three-dimensional structure of the predicted short genes. Data, codes, and models are available at https://github.com/tonytu16/protigeno.
Efficiently Computing Sparse Fourier Transforms of $q$-ary Functions
Jan 15, 2023


Abstract:Fourier transformations of pseudo-Boolean functions are popular tools for analyzing functions of binary sequences. Real-world functions often have structures that manifest in a sparse Fourier transform, and previous works have shown that under the assumption of sparsity the transform can be computed efficiently. But what if we want to compute the Fourier transform of functions defined over a $q$-ary alphabet? These types of functions arise naturally in many areas including biology. A typical workaround is to encode the $q$-ary sequence in binary, however, this approach is computationally inefficient and fundamentally incompatible with the existing sparse Fourier transform techniques. Herein, we develop a sparse Fourier transform algorithm specifically for $q$-ary functions of length $n$ sequences, dubbed $q$-SFT, which provably computes an $S$-sparse transform with vanishing error as $q^n \rightarrow \infty$ in $O(Sn)$ function evaluations and $O(S n^2 \log q)$ computations, where $S = q^{n\delta}$ for some $\delta < 1$. Under certain assumptions, we show that for fixed $q$, a robust version of $q$-SFT has a sample complexity of $O(Sn^2)$ and a computational complexity of $O(Sn^3)$ with the same asymptotic guarantees. We present numerical simulations on synthetic and real-world RNA data, demonstrating the scalability of $q$-SFT to massively high dimensional $q$-ary functions.
Spectral Regularization Allows Data-frugal Learning over Combinatorial Spaces
Oct 05, 2022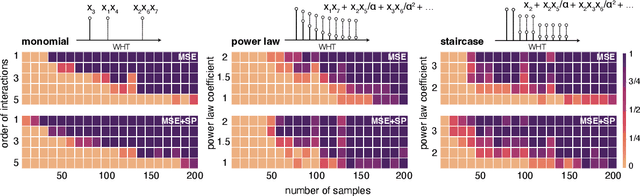
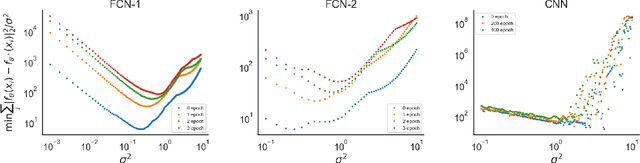
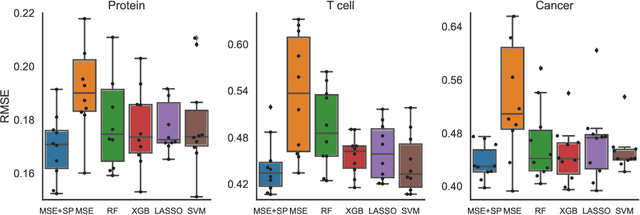
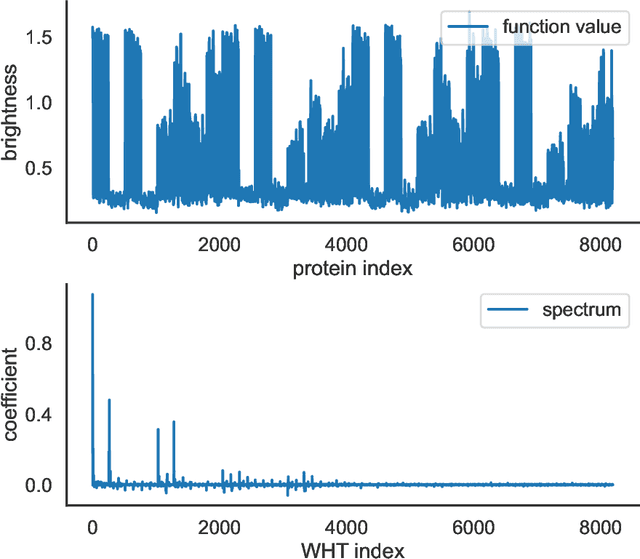
Abstract:Data-driven machine learning models are being increasingly employed in several important inference problems in biology, chemistry, and physics which require learning over combinatorial spaces. Recent empirical evidence (see, e.g., [1], [2], [3]) suggests that regularizing the spectral representation of such models improves their generalization power when labeled data is scarce. However, despite these empirical studies, the theoretical underpinning of when and how spectral regularization enables improved generalization is poorly understood. In this paper, we focus on learning pseudo-Boolean functions and demonstrate that regularizing the empirical mean squared error by the L_1 norm of the spectral transform of the learned function reshapes the loss landscape and allows for data-frugal learning, under a restricted secant condition on the learner's empirical error measured against the ground truth function. Under a weaker quadratic growth condition, we show that stationary points which also approximately interpolate the training data points achieve statistically optimal generalization performance. Complementing our theory, we empirically demonstrate that running gradient descent on the regularized loss results in a better generalization performance compared to baseline algorithms in several data-scarce real-world problems.
Group-Structured Adversarial Training
Jun 18, 2021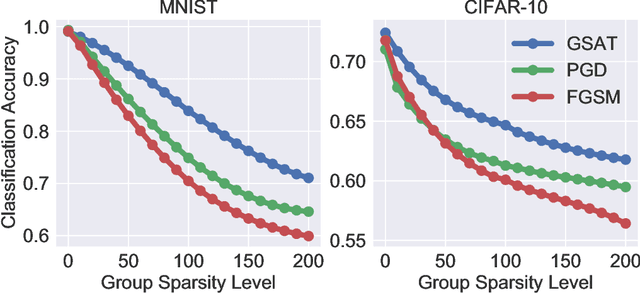
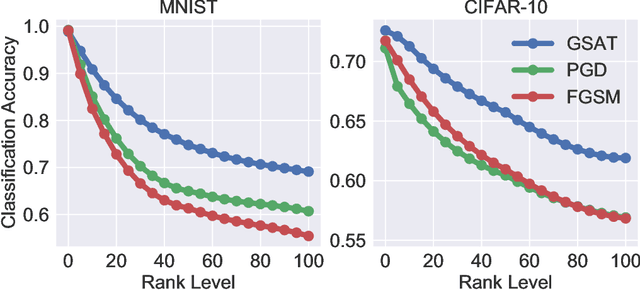
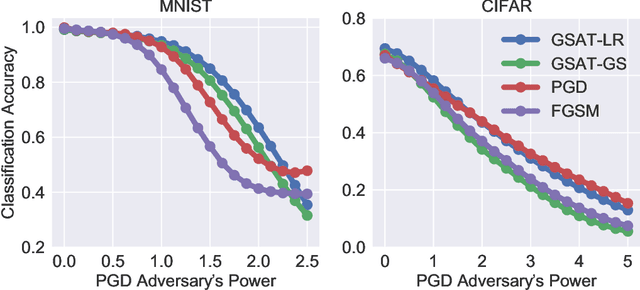
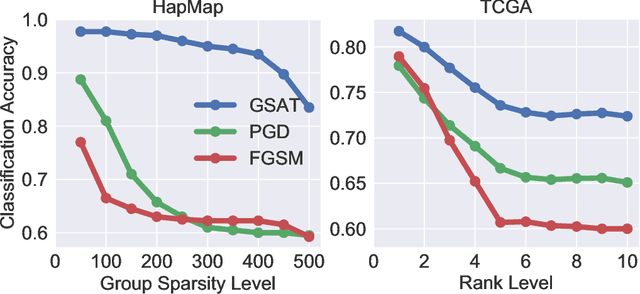
Abstract:Robust training methods against perturbations to the input data have received great attention in the machine learning literature. A standard approach in this direction is adversarial training which learns a model using adversarially-perturbed training samples. However, adversarial training performs suboptimally against perturbations structured across samples such as universal and group-sparse shifts that are commonly present in biological data such as gene expression levels of different tissues. In this work, we seek to close this optimality gap and introduce Group-Structured Adversarial Training (GSAT) which learns a model robust to perturbations structured across samples. We formulate GSAT as a non-convex concave minimax optimization problem which minimizes a group-structured optimal transport cost. Specifically, we focus on the applications of GSAT for group-sparse and rank-constrained perturbations modeled using group and nuclear norm penalties. In order to solve GSAT's non-smooth optimization problem in those cases, we propose a new minimax optimization algorithm called GDADMM by combining Gradient Descent Ascent (GDA) and Alternating Direction Method of Multipliers (ADMM). We present several applications of the GSAT framework to gain robustness against structured perturbations for image recognition and computational biology datasets.
BEAR: Sketching BFGS Algorithm for Ultra-High Dimensional Feature Selection in Sublinear Memory
Oct 26, 2020
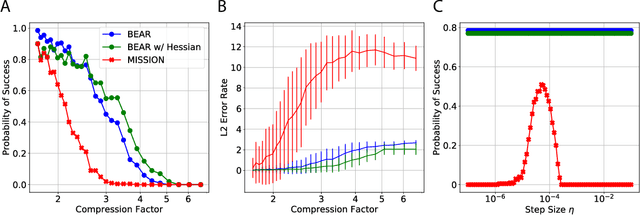

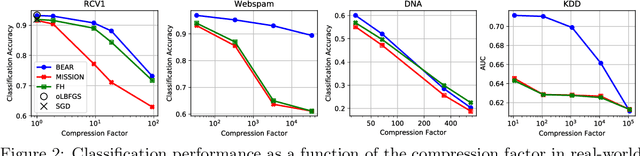
Abstract:We consider feature selection for applications in machine learning where the dimensionality of the data is so large that it exceeds the working memory of the (local) computing machine. Unfortunately, current large-scale sketching algorithms show poor memory-accuracy trade-off due to the irreversible collision and accumulation of the stochastic gradient noise in the sketched domain. Here, we develop a second-order ultra-high dimensional feature selection algorithm, called BEAR, which avoids the extra collisions by storing the second-order gradients in the celebrated Broyden-Fletcher-Goldfarb-Shannon (BFGS) algorithm in Count Sketch, a sublinear memory data structure from the streaming literature. Experiments on real-world data sets demonstrate that BEAR requires up to three orders of magnitude less memory space to achieve the same classification accuracy compared to the first-order sketching algorithms. Theoretical analysis proves convergence of BEAR with rate O(1/t) in t iterations of the sketched algorithm. Our algorithm reveals an unexplored advantage of second-order optimization for memory-constrained sketching of models trained on ultra-high dimensional data sets.
MISSION: Ultra Large-Scale Feature Selection using Count-Sketches
Jun 12, 2018



Abstract:Feature selection is an important challenge in machine learning. It plays a crucial role in the explainability of machine-driven decisions that are rapidly permeating throughout modern society. Unfortunately, the explosion in the size and dimensionality of real-world datasets poses a severe challenge to standard feature selection algorithms. Today, it is not uncommon for datasets to have billions of dimensions. At such scale, even storing the feature vector is impossible, causing most existing feature selection methods to fail. Workarounds like feature hashing, a standard approach to large-scale machine learning, helps with the computational feasibility, but at the cost of losing the interpretability of features. In this paper, we present MISSION, a novel framework for ultra large-scale feature selection that performs stochastic gradient descent while maintaining an efficient representation of the features in memory using a Count-Sketch data structure. MISSION retains the simplicity of feature hashing without sacrificing the interpretability of the features while using only O(log^2(p)) working memory. We demonstrate that MISSION accurately and efficiently performs feature selection on real-world, large-scale datasets with billions of dimensions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge