RandALO: Out-of-sample risk estimation in no time flat

Estimating out-of-sample risk for models trained on large high-dimensional datasets is an expensive but essential part of the machine learning process, enabling practitioners to optimally tune hyperparameters. Cross-validation (CV) serves as the de facto standard for risk estimation but poorly trades off high bias ($K$-fold CV) for computational cost (leave-one-out CV). We propose a randomized approximate leave-one-out (RandALO) risk estimator that is not only a consistent estimator of risk in high dimensions but also less computationally expensive than $K$-fold CV. We support our claims with extensive simulations on synthetic and real data and provide a user-friendly Python package implementing RandALO available on PyPI as randalo and at https://github.com/cvxgrp/randalo.

Fine-grained Analysis and Faster Algorithms for Iteratively Solving Linear Systems

While effective in practice, iterative methods for solving large systems of linear equations can be significantly affected by problem-dependent condition number quantities. This makes characterizing their time complexity challenging, particularly when we wish to make comparisons between deterministic and stochastic methods, that may or may not rely on preconditioning and/or fast matrix multiplication. In this work, we consider a fine-grained notion of complexity for iterative linear solvers which we call the spectral tail condition number, $\kappa_\ell$, defined as the ratio between the $\ell$th largest and the smallest singular value of the matrix representing the system. Concretely, we prove the following main algorithmic result: Given an $n\times n$ matrix $A$ and a vector $b$, we can find $\tilde{x}$ such that $\|A\tilde{x}-b\|\leq\epsilon\|b\|$ in time $\tilde{O}(\kappa_\ell\cdot n^2\log 1/\epsilon)$ for any $\ell = O(n^{\frac1{\omega-1}})=O(n^{0.729})$, where $\omega \approx 2.372$ is the current fast matrix multiplication exponent. This guarantee is achieved by Sketch-and-Project with Nesterov's acceleration. Some of the implications of our result, and of the use of $\kappa_\ell$, include direct improvement over a fine-grained analysis of the Conjugate Gradient method, suggesting a stronger separation between deterministic and stochastic iterative solvers; and relating the complexity of iterative solvers to the ongoing algorithmic advances in fast matrix multiplication, since the bound on $\ell$ improves with $\omega$. Our main technical contributions are new sharp characterizations for the first and second moments of the random projection matrix that commonly arises in sketching algorithms, building on a combination of techniques from combinatorial sampling via determinantal point processes and Gaussian universality results from random matrix theory.

Asymptotically free sketched ridge ensembles: Risks, cross-validation, and tuning

We employ random matrix theory to establish consistency of generalized cross validation (GCV) for estimating prediction risks of sketched ridge regression ensembles, enabling efficient and consistent tuning of regularization and sketching parameters. Our results hold for a broad class of asymptotically free sketches under very mild data assumptions. For squared prediction risk, we provide a decomposition into an unsketched equivalent implicit ridge bias and a sketching-based variance, and prove that the risk can be globally optimized by only tuning sketch size in infinite ensembles. For general subquadratic prediction risk functionals, we extend GCV to construct consistent risk estimators, and thereby obtain distributional convergence of the GCV-corrected predictions in Wasserstein-2 metric. This in particular allows construction of prediction intervals with asymptotically correct coverage conditional on the training data. We also propose an "ensemble trick" whereby the risk for unsketched ridge regression can be efficiently estimated via GCV using small sketched ridge ensembles. We empirically validate our theoretical results using both synthetic and real large-scale datasets with practical sketches including CountSketch and subsampled randomized discrete cosine transforms.

An Adaptive Tangent Feature Perspective of Neural Networks

In order to better understand feature learning in neural networks, we propose a framework for understanding linear models in tangent feature space where the features are allowed to be transformed during training. We consider linear transformations of features, resulting in a joint optimization over parameters and transformations with a bilinear interpolation constraint. We show that this optimization problem has an equivalent linearly constrained optimization with structured regularization that encourages approximately low rank solutions. Specializing to neural network structure, we gain insights into how the features and thus the kernel function change, providing additional nuance to the phenomenon of kernel alignment when the target function is poorly represented using tangent features. In addition to verifying our theoretical observations in real neural networks on a simple regression problem, we empirically show that an adaptive feature implementation of tangent feature classification has an order of magnitude lower sample complexity than the fixed tangent feature model on MNIST and CIFAR-10.

Self-Consuming Generative Models Go MAD

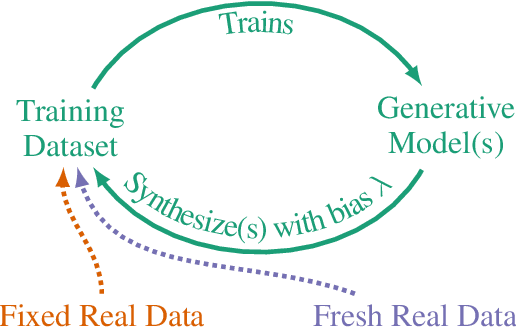
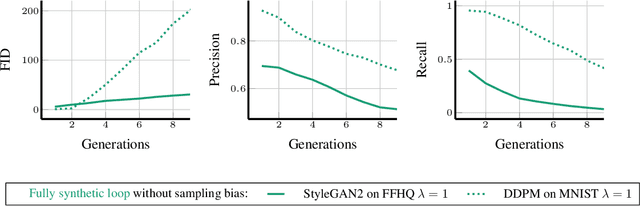
Seismic advances in generative AI algorithms for imagery, text, and other data types has led to the temptation to use synthetic data to train next-generation models. Repeating this process creates an autophagous (self-consuming) loop whose properties are poorly understood. We conduct a thorough analytical and empirical analysis using state-of-the-art generative image models of three families of autophagous loops that differ in how fixed or fresh real training data is available through the generations of training and in whether the samples from previous generation models have been biased to trade off data quality versus diversity. Our primary conclusion across all scenarios is that without enough fresh real data in each generation of an autophagous loop, future generative models are doomed to have their quality (precision) or diversity (recall) progressively decrease. We term this condition Model Autophagy Disorder (MAD), making analogy to mad cow disease.

WIRE: Wavelet Implicit Neural Representations

Implicit neural representations (INRs) have recently advanced numerous vision-related areas. INR performance depends strongly on the choice of the nonlinear activation function employed in its multilayer perceptron (MLP) network. A wide range of nonlinearities have been explored, but, unfortunately, current INRs designed to have high accuracy also suffer from poor robustness (to signal noise, parameter variation, etc.). Inspired by harmonic analysis, we develop a new, highly accurate and robust INR that does not exhibit this tradeoff. Wavelet Implicit neural REpresentation (WIRE) uses a continuous complex Gabor wavelet activation function that is well-known to be optimally concentrated in space-frequency and to have excellent biases for representing images. A wide range of experiments (image denoising, image inpainting, super-resolution, computed tomography reconstruction, image overfitting, and novel view synthesis with neural radiance fields) demonstrate that WIRE defines the new state of the art in INR accuracy, training time, and robustness.

TITAN: Bringing The Deep Image Prior to Implicit Representations

We study the interpolation capabilities of implicit neural representations (INRs) of images. In principle, INRs promise a number of advantages, such as continuous derivatives and arbitrary sampling, being freed from the restrictions of a raster grid. However, empirically, INRs have been observed to poorly interpolate between the pixels of the fit image; in other words, they do not inherently possess a suitable prior for natural images. In this paper, we propose to address and improve INRs' interpolation capabilities by explicitly integrating image prior information into the INR architecture via deep decoder, a specific implementation of the deep image prior (DIP). Our method, which we call TITAN, leverages a residual connection from the input which enables integrating the principles of the grid-based DIP into the grid-free INR. Through super-resolution and computed tomography experiments, we demonstrate that our method significantly improves upon classic INRs, thanks to the induced natural image bias. We also find that by constraining the weights to be sparse, image quality and sharpness are enhanced, increasing the Lipschitz constant.

Benign Overparameterization in Membership Inference with Early Stopping

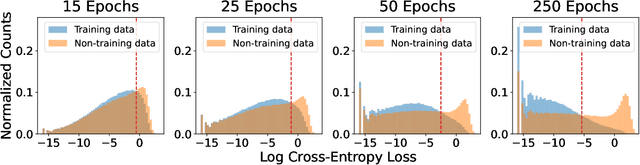
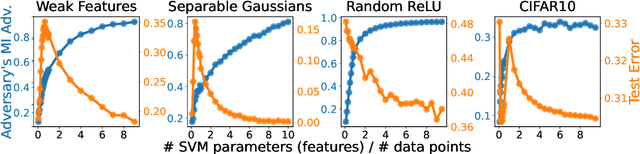
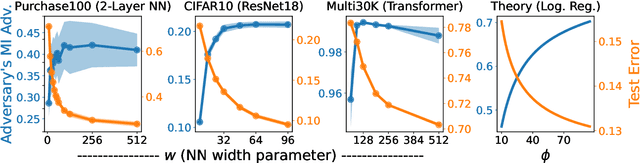
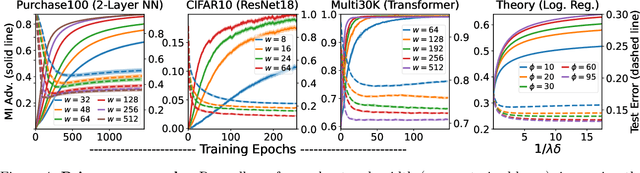
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.

The Flip Side of the Reweighted Coin: Duality of Adaptive Dropout and Regularization

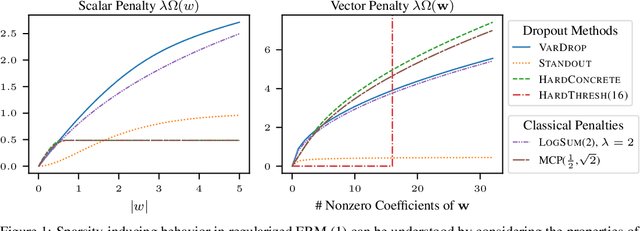
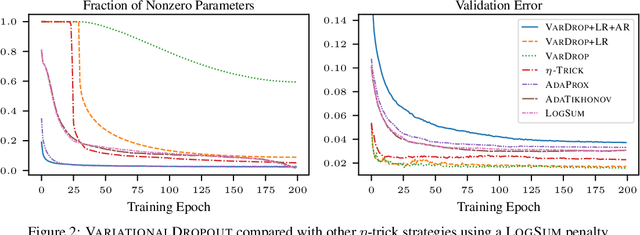
Among the most successful methods for sparsifying deep (neural) networks are those that adaptively mask the network weights throughout training. By examining this masking, or dropout, in the linear case, we uncover a duality between such adaptive methods and regularization through the so-called "$\eta$-trick" that casts both as iteratively reweighted optimizations. We show that any dropout strategy that adapts to the weights in a monotonic way corresponds to an effective subquadratic regularization penalty, and therefore leads to sparse solutions. We obtain the effective penalties for several popular sparsification strategies, which are remarkably similar to classical penalties commonly used in sparse optimization. Considering variational dropout as a case study, we demonstrate similar empirical behavior between the adaptive dropout method and classical methods on the task of deep network sparsification, validating our theory.

Extreme Compressed Sensing of Poisson Rates from Multiple Measurements

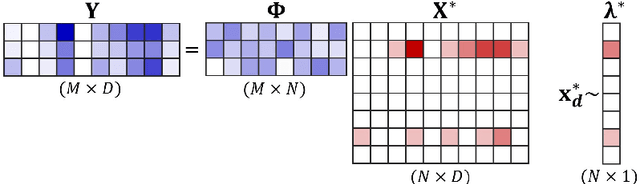
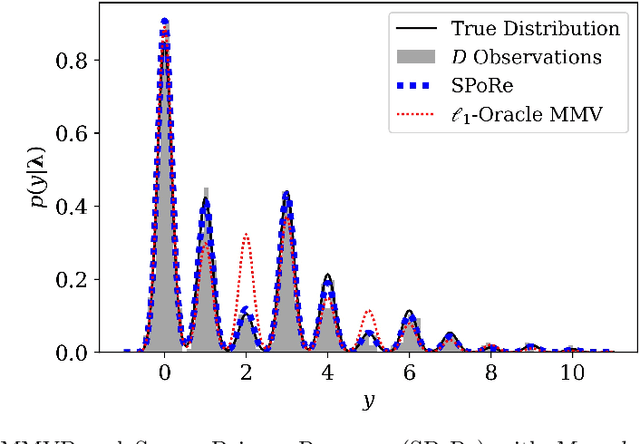
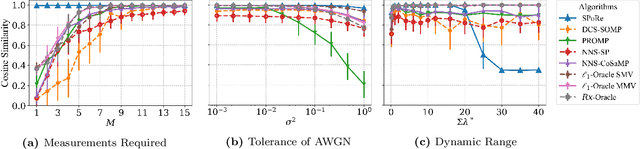
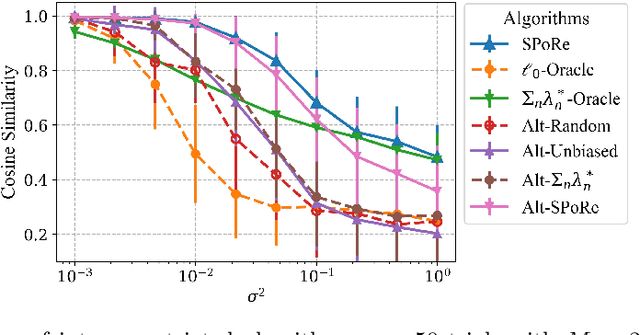
Compressed sensing (CS) is a signal processing technique that enables the efficient recovery of a sparse high-dimensional signal from low-dimensional measurements. In the multiple measurement vector (MMV) framework, a set of signals with the same support must be recovered from their corresponding measurements. Here, we present the first exploration of the MMV problem where signals are independently drawn from a sparse, multivariate Poisson distribution. We are primarily motivated by a suite of biosensing applications of microfluidics where analytes (such as whole cells or biomarkers) are captured in small volume partitions according to a Poisson distribution. We recover the sparse parameter vector of Poisson rates through maximum likelihood estimation with our novel Sparse Poisson Recovery (SPoRe) algorithm. SPoRe uses batch stochastic gradient ascent enabled by Monte Carlo approximations of otherwise intractable gradients. By uniquely leveraging the Poisson structure, SPoRe substantially outperforms a comprehensive set of existing and custom baseline CS algorithms. Notably, SPoRe can exhibit high performance even with one-dimensional measurements and high noise levels. This resource efficiency is not only unprecedented in the field of CS but is also particularly potent for applications in microfluidics in which the number of resolvable measurements per partition is often severely limited. We prove the identifiability property of the Poisson model under such lax conditions, analytically develop insights into system performance, and confirm these insights in simulated experiments. Our findings encourage a new approach to biosensing and are generalizable to other applications featuring spatial and temporal Poisson signals.