Benign Overparameterization in Membership Inference with Early Stopping

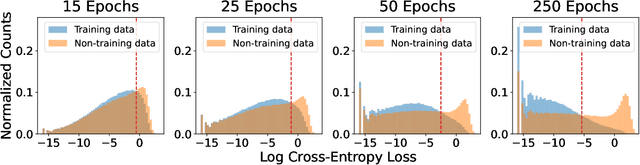
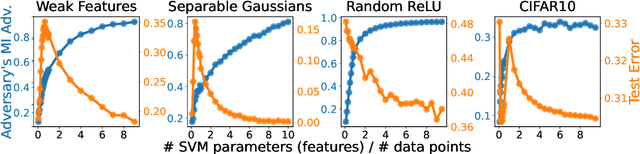
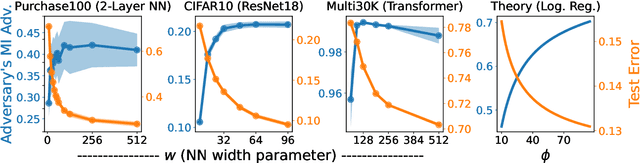
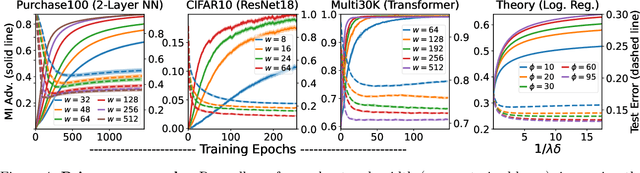
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.

Parameters or Privacy: A Provable Tradeoff Between Overparameterization and Membership Inference

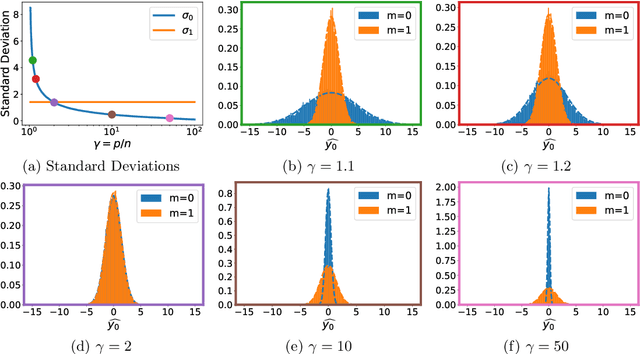
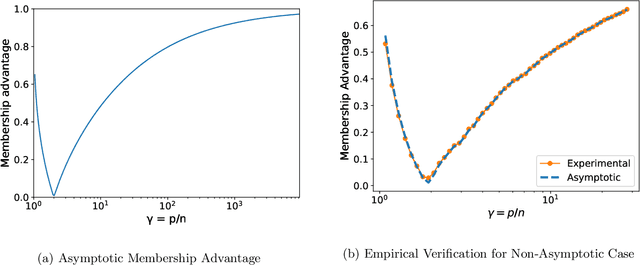
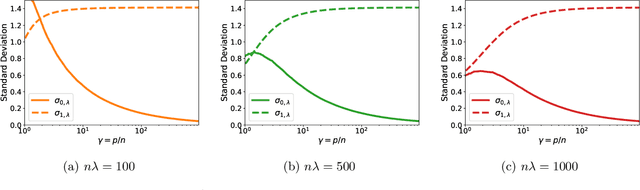
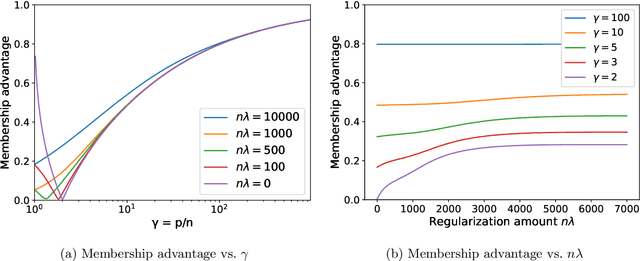
A surprising phenomenon in modern machine learning is the ability of a highly overparameterized model to generalize well (small error on the test data) even when it is trained to memorize the training data (zero error on the training data). This has led to an arms race towards increasingly overparameterized models (c.f., deep learning). In this paper, we study an underexplored hidden cost of overparameterization: the fact that overparameterized models are more vulnerable to privacy attacks, in particular the membership inference attack that predicts the (potentially sensitive) examples used to train a model. We significantly extend the relatively few empirical results on this problem by theoretically proving for an overparameterized linear regression model with Gaussian data that the membership inference vulnerability increases with the number of parameters. Moreover, a range of empirical studies indicates that more complex, nonlinear models exhibit the same behavior. Finally, we study different methods for mitigating such attacks in the overparameterized regime, such as noise addition and regularization, and conclude that simply reducing the parameters of an overparameterized model is an effective strategy to protect it from membership inference without greatly decreasing its generalization error.

The Flip Side of the Reweighted Coin: Duality of Adaptive Dropout and Regularization

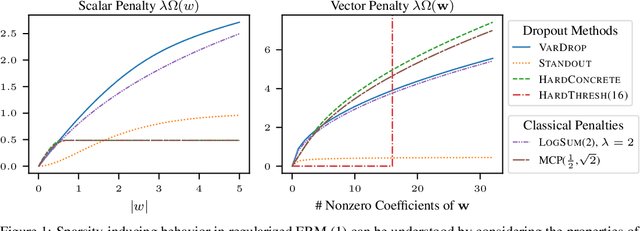
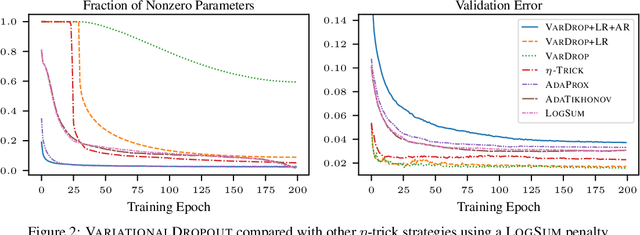
Among the most successful methods for sparsifying deep (neural) networks are those that adaptively mask the network weights throughout training. By examining this masking, or dropout, in the linear case, we uncover a duality between such adaptive methods and regularization through the so-called "$\eta$-trick" that casts both as iteratively reweighted optimizations. We show that any dropout strategy that adapts to the weights in a monotonic way corresponds to an effective subquadratic regularization penalty, and therefore leads to sparse solutions. We obtain the effective penalties for several popular sparsification strategies, which are remarkably similar to classical penalties commonly used in sparse optimization. Considering variational dropout as a case study, we demonstrate similar empirical behavior between the adaptive dropout method and classical methods on the task of deep network sparsification, validating our theory.

The Implicit Regularization of Ordinary Least Squares Ensembles

Ensemble methods that average over a collection of independent predictors that are each limited to a subsampling of both the examples and features of the training data command a significant presence in machine learning, such as the ever-popular random forest, yet the nature of the subsampling effect, particularly of the features, is not well understood. We study the case of an ensemble of linear predictors, where each individual predictor is fit using ordinary least squares on a random submatrix of the data matrix. We show that, under standard Gaussianity assumptions, when the number of features selected for each predictor is optimally tuned, the asymptotic risk of a large ensemble is equal to the asymptotic ridge regression risk, which is known to be optimal among linear predictors in this setting. In addition to eliciting this implicit regularization that results from subsampling, we also connect this ensemble to the dropout technique used in training deep (neural) networks, another strategy that has been shown to have a ridge-like regularizing effect.

A Hessian Based Complexity Measure for Deep Networks

Deep (neural) networks have been applied productively in a wide range of supervised and unsupervised learning tasks. Unlike classical machine learning algorithms, deep networks typically operate in the overparameterized regime, where the number of parameters is larger than the number of training data points. Consequently, understanding the generalization properties and role of (explicit or implicit) regularization in these networks is of great importance. Inspired by the seminal work of Donoho and Grimes in manifold learning, we develop a new measure for the complexity of the function generated by a deep network based on the integral of the norm of the tangent Hessian. This complexity measure can be used to quantify the irregularity of the function a deep network fits to training data or as a regularization penalty for deep network learning. Indeed, we show that the oft-used heuristic of data augmentation imposes an implicit Hessian regularization during learning. We demonstrate the utility of our new complexity measure through a range of learning experiments.

False Discovery Rate Control via Debiased Lasso

We consider the problem of variable selection in high-dimensional statistical models where the goal is to report a set of variables, out of many predictors $X_1, \dotsc, X_p$, that are relevant to a response of interest. For linear high-dimensional model, where the number of parameters exceeds the number of samples $(p>n)$, we propose a procedure for variables selection and prove that it controls the \emph{directional} false discovery rate (FDR) below a pre-assigned significance level $q\in [0,1]$. We further analyze the statistical power of our framework and show that for designs with subgaussian rows and a common precision matrix $\Omega\in\mathbb{R}^{p\times p}$, if the minimum nonzero parameter $\theta_{\min}$ satisfies $$\sqrt{n} \theta_{\min} - \sigma \sqrt{2(\max_{i\in [p]}\Omega_{ii})\log\left(\frac{2p}{qs_0}\right)} \to \infty\,,$$ then this procedure achieves asymptotic power one. Our framework is built upon the debiasing approach and assumes the standard condition $s_0 = o(\sqrt{n}/(\log p)^2)$, where $s_0$ indicates the number of true positives among the $p$ features. Notably, this framework achieves exact directional FDR control without any assumption on the amplitude of unknown regression parameters, and does not require any knowledge of the distribution of covariates or the noise level. We test our method in synthetic and real data experiments to asses its performance and to corroborate our theoretical results.

An Instability in Variational Inference for Topic Models

Topic models are Bayesian models that are frequently used to capture the latent structure of certain corpora of documents or images. Each data element in such a corpus (for instance each item in a collection of scientific articles) is regarded as a convex combination of a small number of vectors corresponding to `topics' or `components'. The weights are assumed to have a Dirichlet prior distribution. The standard approach towards approximating the posterior is to use variational inference algorithms, and in particular a mean field approximation. We show that this approach suffers from an instability that can produce misleading conclusions. Namely, for certain regimes of the model parameters, variational inference outputs a non-trivial decomposition into topics. However --for the same parameter values-- the data contain no actual information about the true decomposition, and hence the output of the algorithm is uncorrelated with the true topic decomposition. Among other consequences, the estimated posterior mean is significantly wrong, and estimated Bayesian credible regions do not achieve the nominal coverage. We discuss how this instability is remedied by more accurate mean field approximations.

Porcupine Neural Networks: (Almost) All Local Optima are Global

Neural networks have been used prominently in several machine learning and statistics applications. In general, the underlying optimization of neural networks is non-convex which makes their performance analysis challenging. In this paper, we take a novel approach to this problem by asking whether one can constrain neural network weights to make its optimization landscape have good theoretical properties while at the same time, be a good approximation for the unconstrained one. For two-layer neural networks, we provide affirmative answers to these questions by introducing Porcupine Neural Networks (PNNs) whose weight vectors are constrained to lie over a finite set of lines. We show that most local optima of PNN optimizations are global while we have a characterization of regions where bad local optimizers may exist. Moreover, our theoretical and empirical results suggest that an unconstrained neural network can be approximated using a polynomially-large PNN.

Non-negative Matrix Factorization via Archetypal Analysis

Given a collection of data points, non-negative matrix factorization (NMF) suggests to express them as convex combinations of a small set of `archetypes' with non-negative entries. This decomposition is unique only if the true archetypes are non-negative and sufficiently sparse (or the weights are sufficiently sparse), a regime that is captured by the separability condition and its generalizations. In this paper, we study an approach to NMF that can be traced back to the work of Cutler and Breiman (1994) and does not require the data to be separable, while providing a generally unique decomposition. We optimize the trade-off between two objectives: we minimize the distance of the data points from the convex envelope of the archetypes (which can be interpreted as an empirical risk), while minimizing the distance of the archetypes from the convex envelope of the data (which can be interpreted as a data-dependent regularization). The archetypal analysis method of (Cutler, Breiman, 1994) is recovered as the limiting case in which the last term is given infinite weight. We introduce a `uniqueness condition' on the data which is necessary for exactly recovering the archetypes from noiseless data. We prove that, under uniqueness (plus additional regularity conditions on the geometry of the archetypes), our estimator is robust. While our approach requires solving a non-convex optimization problem, we find that standard optimization methods succeed in finding good solutions both for real and synthetic data.