WIRE: Wavelet Implicit Neural Representations

Implicit neural representations (INRs) have recently advanced numerous vision-related areas. INR performance depends strongly on the choice of the nonlinear activation function employed in its multilayer perceptron (MLP) network. A wide range of nonlinearities have been explored, but, unfortunately, current INRs designed to have high accuracy also suffer from poor robustness (to signal noise, parameter variation, etc.). Inspired by harmonic analysis, we develop a new, highly accurate and robust INR that does not exhibit this tradeoff. Wavelet Implicit neural REpresentation (WIRE) uses a continuous complex Gabor wavelet activation function that is well-known to be optimally concentrated in space-frequency and to have excellent biases for representing images. A wide range of experiments (image denoising, image inpainting, super-resolution, computed tomography reconstruction, image overfitting, and novel view synthesis with neural radiance fields) demonstrate that WIRE defines the new state of the art in INR accuracy, training time, and robustness.

Benign Overparameterization in Membership Inference with Early Stopping

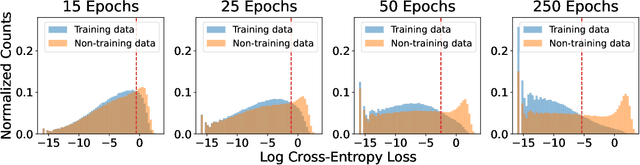
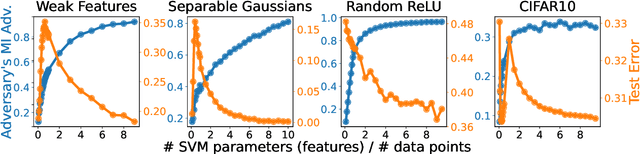
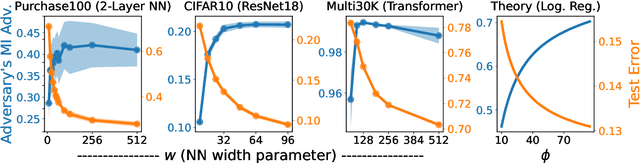
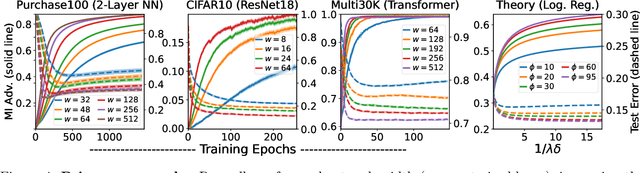
Does a neural network's privacy have to be at odds with its accuracy? In this work, we study the effects the number of training epochs and parameters have on a neural network's vulnerability to membership inference (MI) attacks, which aim to extract potentially private information about the training data. We first demonstrate how the number of training epochs and parameters individually induce a privacy-utility trade-off: more of either improves generalization performance at the expense of lower privacy. However, remarkably, we also show that jointly tuning both can eliminate this privacy-utility trade-off. Specifically, with careful tuning of the number of training epochs, more overparameterization can increase model privacy for fixed generalization error. To better understand these phenomena theoretically, we develop a powerful new leave-one-out analysis tool to study the asymptotic behavior of linear classifiers and apply it to characterize the sample-specific loss threshold MI attack in high-dimensional logistic regression. For practitioners, we introduce a low-overhead procedure to estimate MI risk and tune the number of training epochs to guard against MI attacks.

MINER: Multiscale Implicit Neural Representations

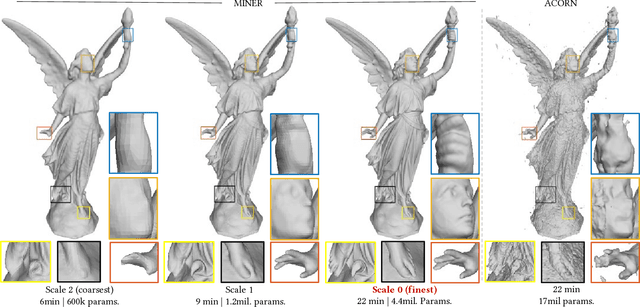
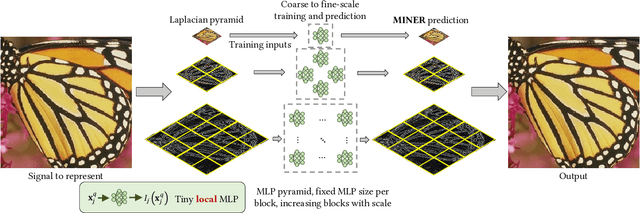
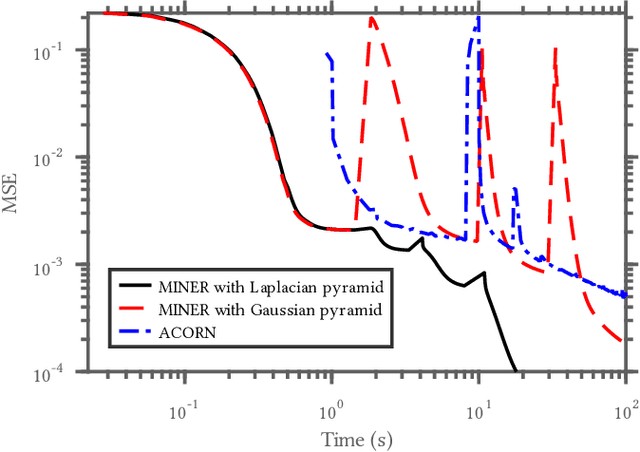
We introduce a new neural signal representation designed for the efficient high-resolution representation of large-scale signals. The key innovation in our multiscale implicit neural representation (MINER) is an internal representation via a Laplacian pyramid, which provides a sparse multiscale representation of the signal that captures orthogonal parts of the signal across scales. We leverage the advantages of the Laplacian pyramid by representing small disjoint patches of the pyramid at each scale with a tiny MLP. This enables the capacity of the network to adaptively increase from coarse to fine scales, and only represent parts of the signal with strong signal energy. The parameters of each MLP are optimized from coarse-to-fine scale which results in faster approximations at coarser scales, thereby ultimately an extremely fast training process. We apply MINER to a range of large-scale signal representation tasks, including gigapixel images and very large point clouds, and demonstrate that it requires fewer than 25% of the parameters, 33% of the memory footprint, and 10% of the computation time of competing techniques such as ACORN to reach the same representation error.

Parameters or Privacy: A Provable Tradeoff Between Overparameterization and Membership Inference

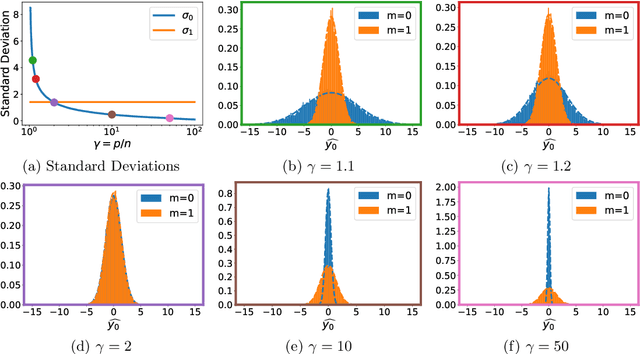
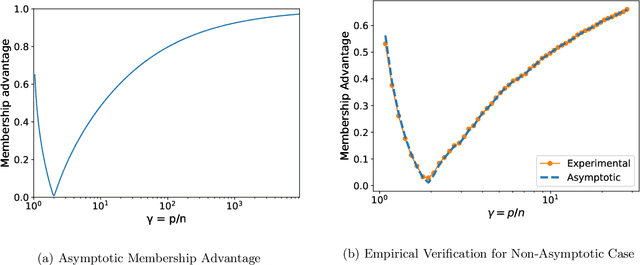
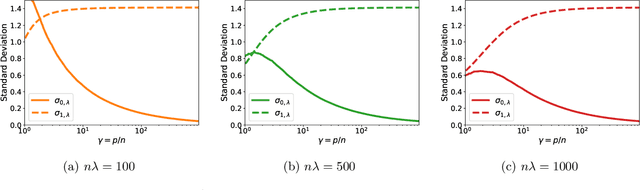
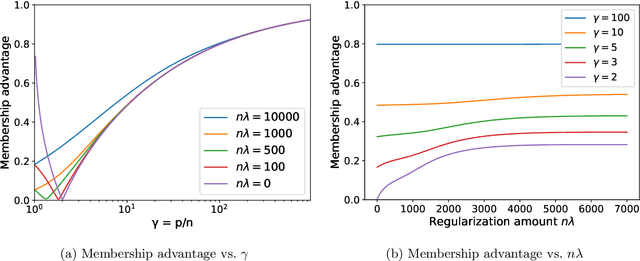
A surprising phenomenon in modern machine learning is the ability of a highly overparameterized model to generalize well (small error on the test data) even when it is trained to memorize the training data (zero error on the training data). This has led to an arms race towards increasingly overparameterized models (c.f., deep learning). In this paper, we study an underexplored hidden cost of overparameterization: the fact that overparameterized models are more vulnerable to privacy attacks, in particular the membership inference attack that predicts the (potentially sensitive) examples used to train a model. We significantly extend the relatively few empirical results on this problem by theoretically proving for an overparameterized linear regression model with Gaussian data that the membership inference vulnerability increases with the number of parameters. Moreover, a range of empirical studies indicates that more complex, nonlinear models exhibit the same behavior. Finally, we study different methods for mitigating such attacks in the overparameterized regime, such as noise addition and regularization, and conclude that simply reducing the parameters of an overparameterized model is an effective strategy to protect it from membership inference without greatly decreasing its generalization error.

Trajectory Prediction & Path Planning for an Object Intercepting UAV with a Mounted Depth Camera

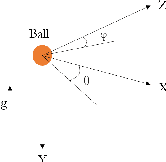
A novel control & software architecture using ROS C++ is introduced for object interception by a UAV with a mounted depth camera and no external aid. Existing work in trajectory prediction focused on the use of off-board tools like motion capture rooms to intercept thrown objects. The present study designs the UAV architecture to be completely on-board capable of object interception with the use of a depth camera and point cloud processing. The architecture uses an iterative trajectory prediction algorithm for non-propelled objects like a ping-pong ball. A variety of path planning approaches to object interception and their corresponding scenarios are discussed, evaluated & simulated in Gazebo. The successful simulations exemplify the potential of using the proposed architecture for the on-board autonomy of UAVs intercepting objects.

Wearing a MASK: Compressed Representations of Variable-Length Sequences Using Recurrent Neural Tangent Kernels

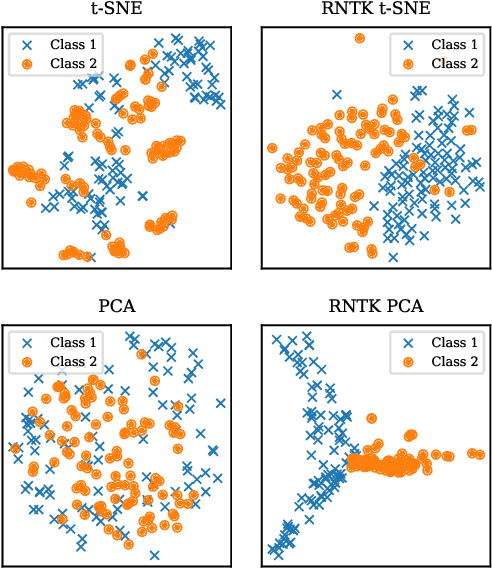
High dimensionality poses many challenges to the use of data, from visualization and interpretation, to prediction and storage for historical preservation. Techniques abound to reduce the dimensionality of fixed-length sequences, yet these methods rarely generalize to variable-length sequences. To address this gap, we extend existing methods that rely on the use of kernels to variable-length sequences via use of the Recurrent Neural Tangent Kernel (RNTK). Since a deep neural network with ReLu activation is a Max-Affine Spline Operator (MASO), we dub our approach Max-Affine Spline Kernel (MASK). We demonstrate how MASK can be used to extend principal components analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) and apply these new algorithms to separate synthetic time series data sampled from second-order differential equations.