When are Diffusion Priors Helpful in Sparse Reconstruction? A Study with Sparse-view CT

Diffusion models demonstrate state-of-the-art performance on image generation, and are gaining traction for sparse medical image reconstruction tasks. However, compared to classical reconstruction algorithms relying on simple analytical priors, diffusion models have the dangerous property of producing realistic looking results \emph{even when incorrect}, particularly with few observations. We investigate the utility of diffusion models as priors for image reconstruction by varying the number of observations and comparing their performance to classical priors (sparse and Tikhonov regularization) using pixel-based, structural, and downstream metrics. We make comparisons on low-dose chest wall computed tomography (CT) for fat mass quantification. First, we find that classical priors are superior to diffusion priors when the number of projections is ``sufficient''. Second, we find that diffusion priors can capture a large amount of detail with very few observations, significantly outperforming classical priors. However, they fall short of capturing all details, even with many observations. Finally, we find that the performance of diffusion priors plateau after extremely few ($\approx$10-15) projections. Ultimately, our work highlights potential issues with diffusion-based sparse reconstruction and underscores the importance of further investigation, particularly in high-stakes clinical settings.

Regression Conformal Prediction under Bias

Uncertainty quantification is crucial to account for the imperfect predictions of machine learning algorithms for high-impact applications. Conformal prediction (CP) is a powerful framework for uncertainty quantification that generates calibrated prediction intervals with valid coverage. In this work, we study how CP intervals are affected by bias - the systematic deviation of a prediction from ground truth values - a phenomenon prevalent in many real-world applications. We investigate the influence of bias on interval lengths of two different types of adjustments -- symmetric adjustments, the conventional method where both sides of the interval are adjusted equally, and asymmetric adjustments, a more flexible method where the interval can be adjusted unequally in positive or negative directions. We present theoretical and empirical analyses characterizing how symmetric and asymmetric adjustments impact the "tightness" of CP intervals for regression tasks. Specifically for absolute residual and quantile-based non-conformity scores, we prove: 1) the upper bound of symmetrically adjusted interval lengths increases by $2|b|$ where $b$ is a globally applied scalar value representing bias, 2) asymmetrically adjusted interval lengths are not affected by bias, and 3) conditions when asymmetrically adjusted interval lengths are guaranteed to be smaller than symmetric ones. Our analyses suggest that even if predictions exhibit significant drift from ground truth values, asymmetrically adjusted intervals are still able to maintain the same tightness and validity of intervals as if the drift had never happened, while symmetric ones significantly inflate the lengths. We demonstrate our theoretical results with two real-world prediction tasks: sparse-view computed tomography (CT) reconstruction and time-series weather forecasting. Our work paves the way for more bias-robust machine learning systems.

Wearing a MASK: Compressed Representations of Variable-Length Sequences Using Recurrent Neural Tangent Kernels

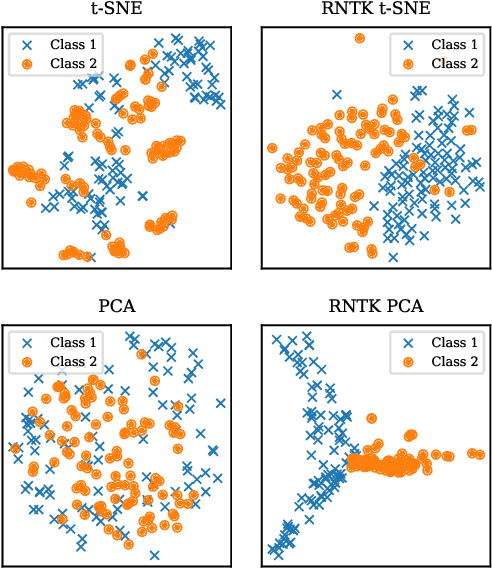
High dimensionality poses many challenges to the use of data, from visualization and interpretation, to prediction and storage for historical preservation. Techniques abound to reduce the dimensionality of fixed-length sequences, yet these methods rarely generalize to variable-length sequences. To address this gap, we extend existing methods that rely on the use of kernels to variable-length sequences via use of the Recurrent Neural Tangent Kernel (RNTK). Since a deep neural network with ReLu activation is a Max-Affine Spline Operator (MASO), we dub our approach Max-Affine Spline Kernel (MASK). We demonstrate how MASK can be used to extend principal components analysis (PCA) and t-distributed stochastic neighbor embedding (t-SNE) and apply these new algorithms to separate synthetic time series data sampled from second-order differential equations.