Lorenzo Luzi
GRR-CoCa: Leveraging LLM Mechanisms in Multimodal Model Architectures
Jul 24, 2025Abstract:State-of-the-art (SOTA) image and text generation models are multimodal models that have many similarities to large language models (LLMs). Despite achieving strong performances, leading foundational multimodal model architectures frequently lag behind the architectural sophistication of contemporary LLMs. We propose GRR-CoCa, an improved SOTA Contrastive Captioner (CoCa) model that incorporates Gaussian error gated linear units, root mean squared normalization, and rotary positional embedding into the textual decoders and the vision transformer (ViT) encoder. Each architectural modification has been shown to improve model performance in LLMs, but has yet to be adopted in CoCa. We benchmarked GRR-CoCa against Baseline CoCa, a model with the same modified textual decoders but with CoCa's original ViT encoder. We used standard pretraining and fine-tuning workflows to benchmark the models on contrastive and generative tasks. Our GRR-CoCa significantly outperformed Baseline CoCa on the pretraining dataset and three diverse fine-tuning datasets. Pretraining improvements were 27.25% in contrastive loss, 3.71% in perplexity, and 7.15% in CoCa loss. The average fine-tuning improvements were 13.66% in contrastive loss, 5.18% in perplexity, and 5.55% in CoCa loss. We show that GRR-CoCa's modified architecture improves performance and generalization across vision-language domains.
EMulator: Rapid Estimation of Complex-valued Electric Fields using a U-Net Architecture
May 04, 2025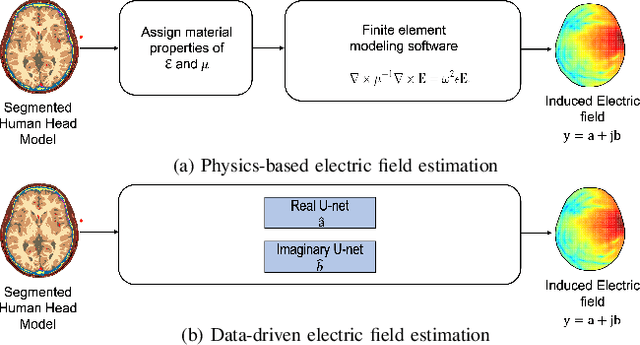

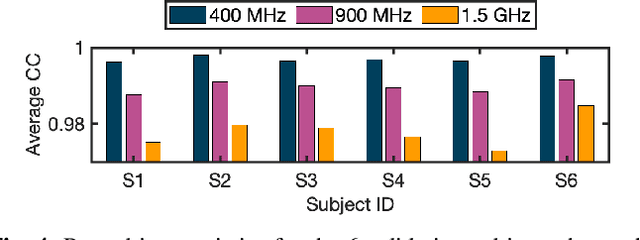
Abstract:A common factor across electromagnetic methodologies of brain stimulation is the optimization of essential dosimetry parameters, like amplitude, phase, and location of one or more transducers, which controls the stimulation strength and targeting precision. Since obtaining in-vivo measurements for the electric field distribution inside the biological tissue is challenging, physics-based simulators are used. However, these simulators are computationally expensive and time-consuming, making repeated calculations of electric fields for optimization purposes computationally prohibitive. To overcome this issue, we developed EMulator, a U-Net architecture-based regression model, for fast and robust complex electric field estimation. We trained EMulator using electric fields generated by 43 antennas placed around 14 segmented human brain models. Once trained, EMulator uses a segmented human brain model with an antenna location as an input and outputs the corresponding electric field. A representative result of our study is that, at 1.5 GHz, on the validation dataset consisting of 6 subjects, we can estimate the electric field with the magnitude of complex correlation coefficient of 0.978. Additionally, we could calculate the electric field with a mean time of 4.4 ms. On average, this is at least x1200 faster than the time required by state-of-the-art physics-based simulator COMSOL. The significance of this work is that it shows the possibility of real-time calculation of the electric field from the segmented human head model and antenna location, making it possible to optimize the amplitude, phase, and location of several different transducers with stochastic gradient descent since our model is almost everywhere differentiable.
Removing Bias from Maximum Likelihood Estimation with Model Autophagy
May 22, 2024Abstract:We propose autophagy penalized likelihood estimation (PLE), an unbiased alternative to maximum likelihood estimation (MLE) which is more fair and less susceptible to model autophagy disorder (madness). Model autophagy refers to models trained on their own output; PLE ensures the statistics of these outputs coincide with the data statistics. This enables PLE to be statistically unbiased in certain scenarios where MLE is biased. When biased, MLE unfairly penalizes minority classes in unbalanced datasets and exacerbates the recently discovered issue of self-consuming generative modeling. Theoretical and empirical results show that 1) PLE is more fair to minority classes and 2) PLE is more stable in a self-consumed setting. Furthermore, we provide a scalable and portable implementation of PLE with a hypernetwork framework, allowing existing deep learning architectures to be easily trained with PLE. Finally, we show PLE can bridge the gap between Bayesian and frequentist paradigms in statistics.
Using Higher-Order Moments to Assess the Quality of GAN-generated Image Features
Oct 31, 2023Abstract:The rapid advancement of Generative Adversarial Networks (GANs) necessitates the need to robustly evaluate these models. Among the established evaluation criteria, the Fr\'{e}chet Inception Distance (FID) has been widely adopted due to its conceptual simplicity, fast computation time, and strong correlation with human perception. However, FID has inherent limitations, mainly stemming from its assumption that feature embeddings follow a Gaussian distribution, and therefore can be defined by their first two moments. As this does not hold in practice, in this paper we explore the importance of third-moments in image feature data and use this information to define a new measure, which we call the Skew Inception Distance (SID). We prove that SID is a pseudometric on probability distributions, show how it extends FID, and present a practical method for its computation. Our numerical experiments support that SID either tracks with FID or, in some cases, aligns more closely with human perception when evaluating image features of ImageNet data.
Self-Consuming Generative Models Go MAD
Jul 04, 2023

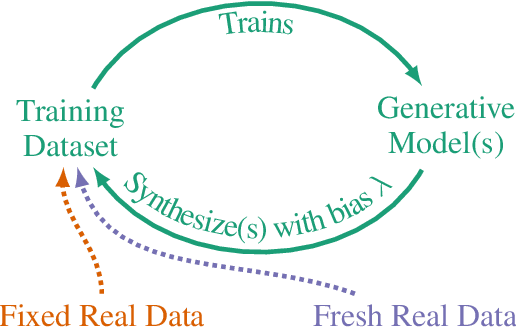
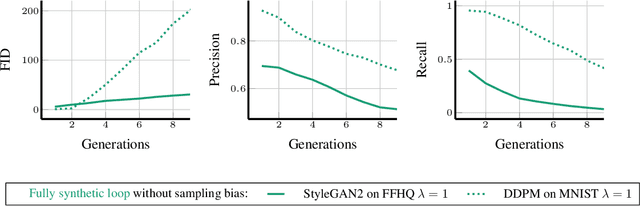
Abstract:Seismic advances in generative AI algorithms for imagery, text, and other data types has led to the temptation to use synthetic data to train next-generation models. Repeating this process creates an autophagous (self-consuming) loop whose properties are poorly understood. We conduct a thorough analytical and empirical analysis using state-of-the-art generative image models of three families of autophagous loops that differ in how fixed or fresh real training data is available through the generations of training and in whether the samples from previous generation models have been biased to trade off data quality versus diversity. Our primary conclusion across all scenarios is that without enough fresh real data in each generation of an autophagous loop, future generative models are doomed to have their quality (precision) or diversity (recall) progressively decrease. We term this condition Model Autophagy Disorder (MAD), making analogy to mad cow disease.
Overfreezing Meets Overparameterization: A Double Descent Perspective on Transfer Learning of Deep Neural Networks
Nov 20, 2022Abstract:We study the generalization behavior of transfer learning of deep neural networks (DNNs). We adopt the overparameterization perspective -- featuring interpolation of the training data (i.e., approximately zero train error) and the double descent phenomenon -- to explain the delicate effect of the transfer learning setting on generalization performance. We study how the generalization behavior of transfer learning is affected by the dataset size in the source and target tasks, the number of transferred layers that are kept frozen in the target DNN training, and the similarity between the source and target tasks. We show that the test error evolution during the target DNN training has a more significant double descent effect when the target training dataset is sufficiently large with some label noise. In addition, a larger source training dataset can delay the arrival to interpolation and double descent peak in the target DNN training. Moreover, we demonstrate that the number of frozen layers can determine whether the transfer learning is effectively underparameterized or overparameterized and, in turn, this may affect the relative success or failure of learning. Specifically, we show that too many frozen layers may make a transfer from a less related source task better or on par with a transfer from a more related source task; we call this case overfreezing. We establish our results using image classification experiments with the residual network (ResNet) and vision transformer (ViT) architectures.
TITAN: Bringing The Deep Image Prior to Implicit Representations
Nov 01, 2022Abstract:We study the interpolation capabilities of implicit neural representations (INRs) of images. In principle, INRs promise a number of advantages, such as continuous derivatives and arbitrary sampling, being freed from the restrictions of a raster grid. However, empirically, INRs have been observed to poorly interpolate between the pixels of the fit image; in other words, they do not inherently possess a suitable prior for natural images. In this paper, we propose to address and improve INRs' interpolation capabilities by explicitly integrating image prior information into the INR architecture via deep decoder, a specific implementation of the deep image prior (DIP). Our method, which we call TITAN, leverages a residual connection from the input which enables integrating the principles of the grid-based DIP into the grid-free INR. Through super-resolution and computed tomography experiments, we demonstrate that our method significantly improves upon classic INRs, thanks to the induced natural image bias. We also find that by constraining the weights to be sparse, image quality and sharpness are enhanced, increasing the Lipschitz constant.
NFT-K: Non-Fungible Tangent Kernels
Oct 11, 2021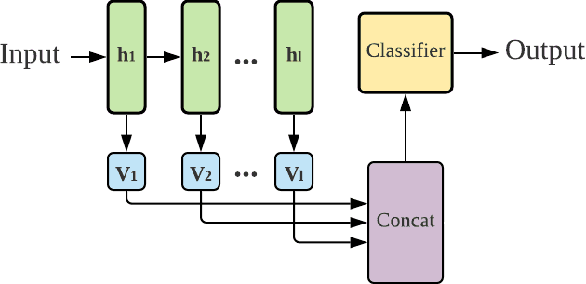
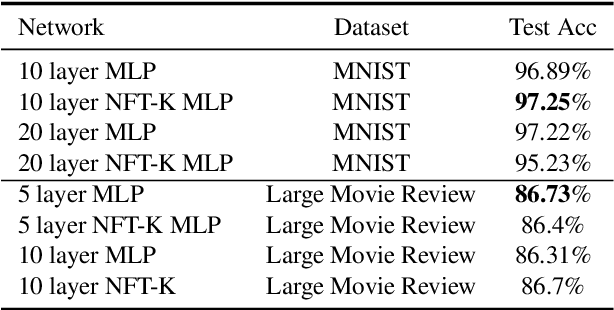
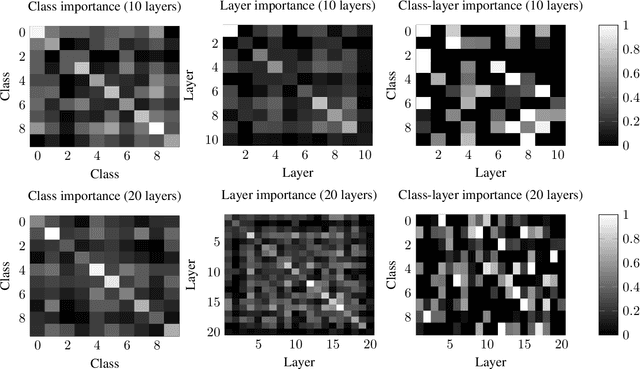
Abstract:Deep neural networks have become essential for numerous applications due to their strong empirical performance such as vision, RL, and classification. Unfortunately, these networks are quite difficult to interpret, and this limits their applicability in settings where interpretability is important for safety, such as medical imaging. One type of deep neural network is neural tangent kernel that is similar to a kernel machine that provides some aspect of interpretability. To further contribute interpretability with respect to classification and the layers, we develop a new network as a combination of multiple neural tangent kernels, one to model each layer of the deep neural network individually as opposed to past work which attempts to represent the entire network via a single neural tangent kernel. We demonstrate the interpretability of this model on two datasets, showing that the multiple kernels model elucidates the interplay between the layers and predictions.
Evaluating generative networks using Gaussian mixtures of image features
Oct 08, 2021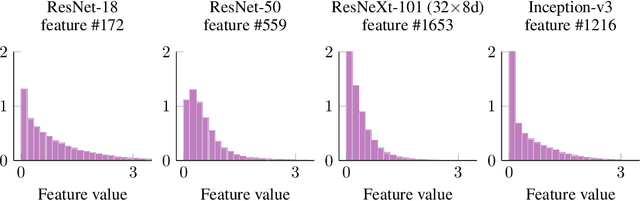

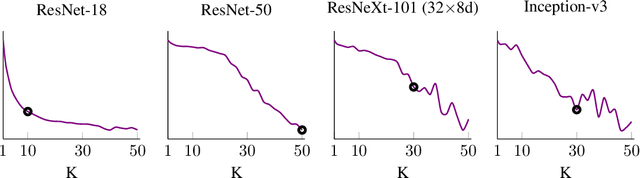

Abstract:We develop a measure for evaluating the performance of generative networks given two sets of images. A popular performance measure currently used to do this is the Fr\'echet Inception Distance (FID). However, FID assumes that images featurized using the penultimate layer of Inception-v3 follow a Gaussian distribution. This assumption allows FID to be easily computed, since FID uses the 2-Wasserstein distance of two Gaussian distributions fitted to the featurized images. However, we show that Inception-v3 features of the ImageNet dataset are not Gaussian; in particular, each marginal is not Gaussian. To remedy this problem, we model the featurized images using Gaussian mixture models (GMMs) and compute the 2-Wasserstein distance restricted to GMMs. We define a performance measure, which we call WaM, on two sets of images by using Inception-v3 (or another classifier) to featurize the images, estimate two GMMs, and use the restricted 2-Wasserstein distance to compare the GMMs. We experimentally show the advantages of WaM over FID, including how FID is more sensitive than WaM to image perturbations. By modelling the non-Gaussian features obtained from Inception-v3 as GMMs and using a GMM metric, we can more accurately evaluate generative network performance.
Double Descent and Other Interpolation Phenomena in GANs
Jun 07, 2021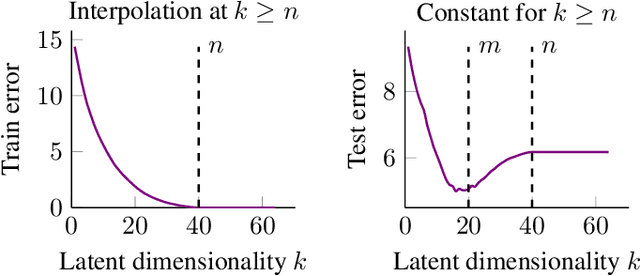
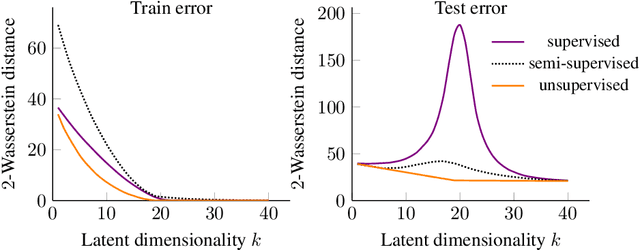
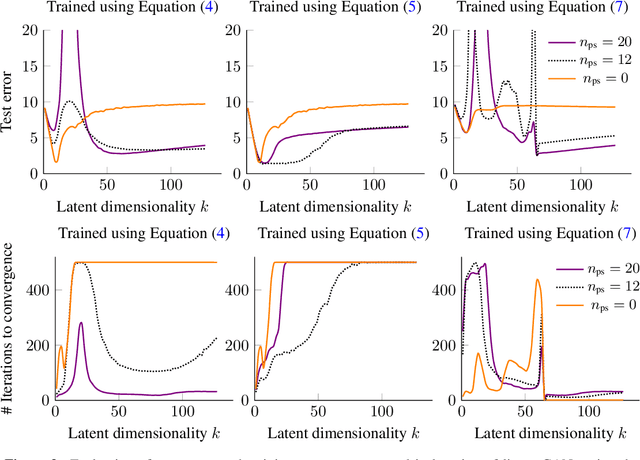
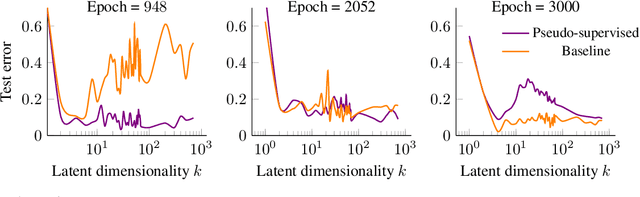
Abstract:We study overparameterization in generative adversarial networks (GANs) that can interpolate the training data. We show that overparameterization can improve generalization performance and accelerate the training process. We study the generalization error as a function of latent space dimension and identify two main behaviors, depending on the learning setting. First, we show that overparameterized generative models that learn distributions by minimizing a metric or $f$-divergence do not exhibit double descent in generalization errors; specifically, all the interpolating solutions achieve the same generalization error. Second, we develop a new pseudo-supervised learning approach for GANs where the training utilizes pairs of fabricated (noise) inputs in conjunction with real output samples. Our pseudo-supervised setting exhibits double descent (and in some cases, triple descent) of generalization errors. We combine pseudo-supervision with overparameterization (i.e., overly large latent space dimension) to accelerate training while performing better, or close to, the generalization performance without pseudo-supervision. While our analysis focuses mostly on linear GANs, we also apply important insights for improving generalization of nonlinear, multilayer GANs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge