How Does Overparameterization Affect Machine Unlearning of Deep Neural Networks?

Machine unlearning is the task of updating a trained model to forget specific training data without retraining from scratch. In this paper, we investigate how unlearning of deep neural networks (DNNs) is affected by the model parameterization level, which corresponds here to the DNN width. We define validation-based tuning for several unlearning methods from the recent literature, and show how these methods perform differently depending on (i) the DNN parameterization level, (ii) the unlearning goal (unlearned data privacy or bias removal), (iii) whether the unlearning method explicitly uses the unlearned examples. Our results show that unlearning excels on overparameterized models, in terms of balancing between generalization and achieving the unlearning goal; although for bias removal this requires the unlearning method to use the unlearned examples. We further elucidate our error-based analysis by measuring how much the unlearning changes the classification decision regions in the proximity of the unlearned examples, and avoids changing them elsewhere. By this we show that the unlearning success for overparameterized models stems from the ability to delicately change the model functionality in small regions in the input space while keeping much of the model functionality unchanged.

TL-PCA: Transfer Learning of Principal Component Analysis

Principal component analysis (PCA) can be significantly limited when there is too few examples of the target data of interest. We propose a transfer learning approach to PCA (TL-PCA) where knowledge from a related source task is used in addition to the scarce data of a target task. Our TL-PCA has two versions, one that uses a pretrained PCA solution of the source task, and another that uses the source data. Our proposed approach extends the PCA optimization objective with a penalty on the proximity of the target subspace and the source subspace as given by the pretrained source model or the source data. This optimization is solved by eigendecomposition for which the number of data-dependent eigenvectors (i.e., principal directions of TL-PCA) is not limited to the number of target data examples, which is a root cause that limits the standard PCA performance. Accordingly, our results for image datasets show that the representation of test data is improved by TL-PCA for dimensionality reduction where the learned subspace dimension is lower or higher than the number of target data examples.

How Does Perfect Fitting Affect Representation Learning? On the Training Dynamics of Representations in Deep Neural Networks

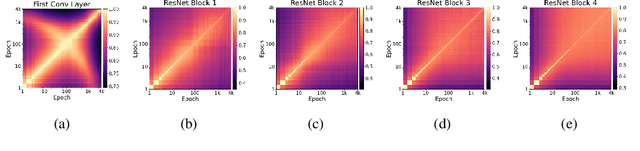
In this paper, we elucidate how representations in deep neural networks (DNNs) evolve during training. We focus on overparameterized learning settings where the training continues much after the trained DNN starts to perfectly fit its training data. We examine the evolution of learned representations along the entire training process, including its perfect fitting regime, and with respect to the epoch-wise double descent phenomenon. We explore the representational similarity of DNN layers, each layer with respect to its own representations throughout the training process. For this, we use two similarity metrics: (1) The centered kernel alignment (CKA) similarity; (2) Similarity of decision regions of linear classifier probes that we train for the DNN layers. Our extensive experiments discover training dynamics patterns that can emerge in layers depending on the relative layer-depth, DNN width, and architecture. We show that representations at the deeper layers evolve much more in the training when an epoch-wise double descent occurs. For Vision Transformer, we show that the perfect fitting threshold creates a transition in the evolution of representations across all the encoder blocks.

Recovery of Training Data from Overparameterized Autoencoders: An Inverse Problem Perspective

We study the recovery of training data from overparameterized autoencoder models. Given a degraded training sample, we define the recovery of the original sample as an inverse problem and formulate it as an optimization task. In our inverse problem, we use the trained autoencoder to implicitly define a regularizer for the particular training dataset that we aim to retrieve from. We develop the intricate optimization task into a practical method that iteratively applies the trained autoencoder and relatively simple computations that estimate and address the unknown degradation operator. We evaluate our method for blind inpainting where the goal is to recover training images from degradation of many missing pixels in an unknown pattern. We examine various deep autoencoder architectures, such as fully connected and U-Net (with various nonlinearities and at diverse train loss values), and show that our method significantly outperforms previous methods for training data recovery from autoencoders. Importantly, our method greatly improves the recovery performance also in settings that were previously considered highly challenging, and even impractical, for such retrieval.

Overfreezing Meets Overparameterization: A Double Descent Perspective on Transfer Learning of Deep Neural Networks

We study the generalization behavior of transfer learning of deep neural networks (DNNs). We adopt the overparameterization perspective -- featuring interpolation of the training data (i.e., approximately zero train error) and the double descent phenomenon -- to explain the delicate effect of the transfer learning setting on generalization performance. We study how the generalization behavior of transfer learning is affected by the dataset size in the source and target tasks, the number of transferred layers that are kept frozen in the target DNN training, and the similarity between the source and target tasks. We show that the test error evolution during the target DNN training has a more significant double descent effect when the target training dataset is sufficiently large with some label noise. In addition, a larger source training dataset can delay the arrival to interpolation and double descent peak in the target DNN training. Moreover, we demonstrate that the number of frozen layers can determine whether the transfer learning is effectively underparameterized or overparameterized and, in turn, this may affect the relative success or failure of learning. Specifically, we show that too many frozen layers may make a transfer from a less related source task better or on par with a transfer from a more related source task; we call this case overfreezing. We establish our results using image classification experiments with the residual network (ResNet) and vision transformer (ViT) architectures.

Can Neural Nets Learn the Same Model Twice? Investigating Reproducibility and Double Descent from the Decision Boundary Perspective

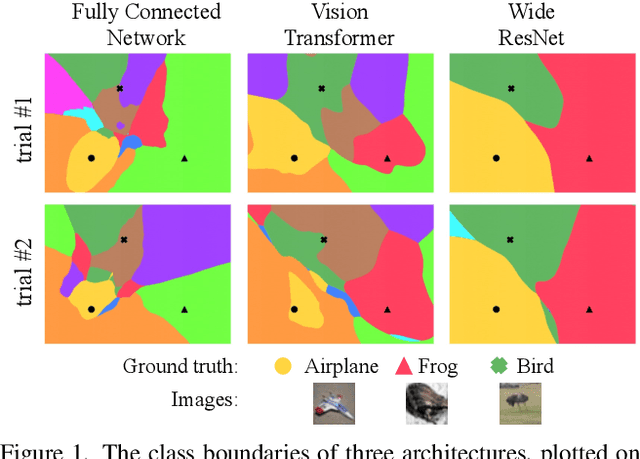
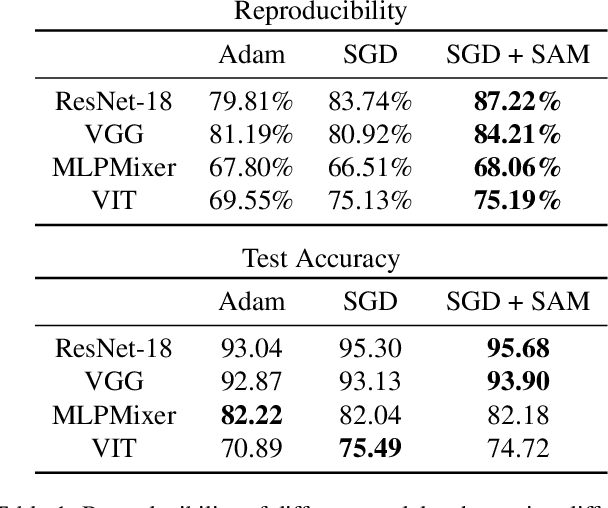
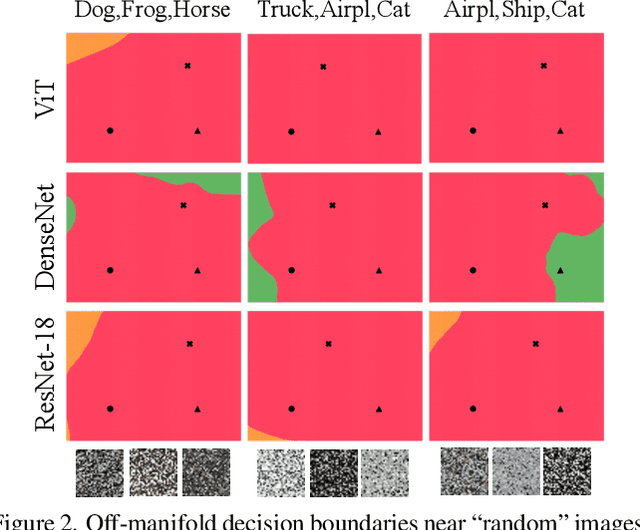
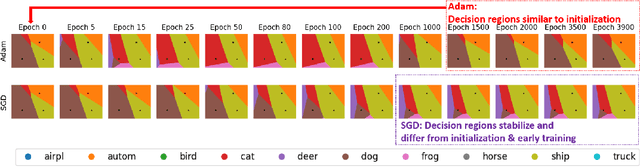
We discuss methods for visualizing neural network decision boundaries and decision regions. We use these visualizations to investigate issues related to reproducibility and generalization in neural network training. We observe that changes in model architecture (and its associate inductive bias) cause visible changes in decision boundaries, while multiple runs with the same architecture yield results with strong similarities, especially in the case of wide architectures. We also use decision boundary methods to visualize double descent phenomena. We see that decision boundary reproducibility depends strongly on model width. Near the threshold of interpolation, neural network decision boundaries become fragmented into many small decision regions, and these regions are non-reproducible. Meanwhile, very narrows and very wide networks have high levels of reproducibility in their decision boundaries with relatively few decision regions. We discuss how our observations relate to the theory of double descent phenomena in convex models. Code is available at https://github.com/somepago/dbViz

A Farewell to the Bias-Variance Tradeoff? An Overview of the Theory of Overparameterized Machine Learning

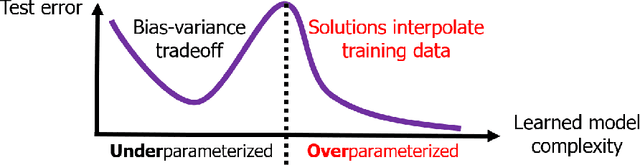
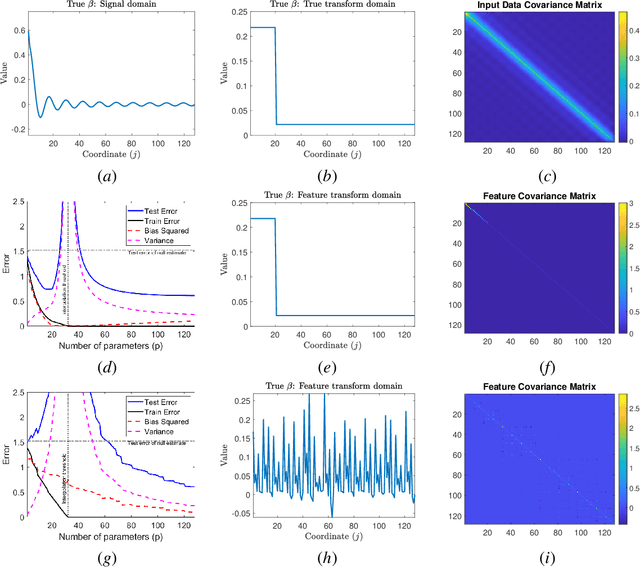
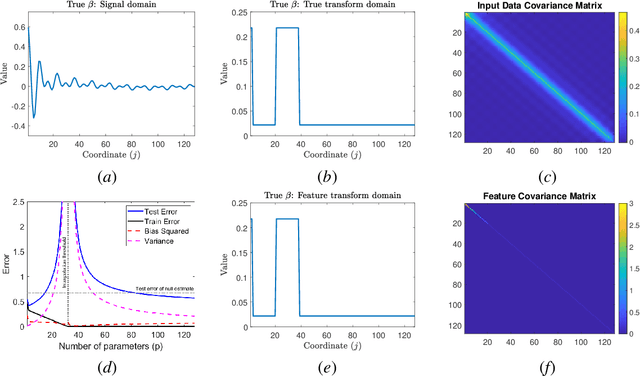
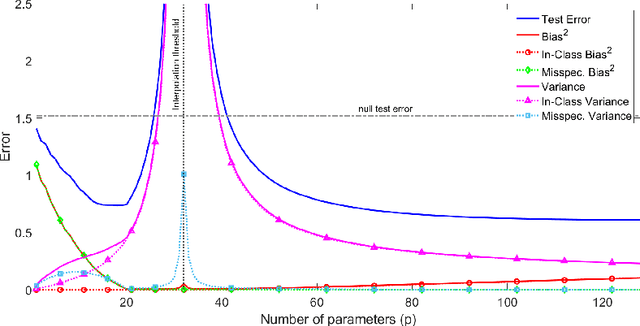
The rapid recent progress in machine learning (ML) has raised a number of scientific questions that challenge the longstanding dogma of the field. One of the most important riddles is the good empirical generalization of overparameterized models. Overparameterized models are excessively complex with respect to the size of the training dataset, which results in them perfectly fitting (i.e., interpolating) the training data, which is usually noisy. Such interpolation of noisy data is traditionally associated with detrimental overfitting, and yet a wide range of interpolating models -- from simple linear models to deep neural networks -- have recently been observed to generalize extremely well on fresh test data. Indeed, the recently discovered double descent phenomenon has revealed that highly overparameterized models often improve over the best underparameterized model in test performance. Understanding learning in this overparameterized regime requires new theory and foundational empirical studies, even for the simplest case of the linear model. The underpinnings of this understanding have been laid in very recent analyses of overparameterized linear regression and related statistical learning tasks, which resulted in precise analytic characterizations of double descent. This paper provides a succinct overview of this emerging theory of overparameterized ML (henceforth abbreviated as TOPML) that explains these recent findings through a statistical signal processing perspective. We emphasize the unique aspects that define the TOPML research area as a subfield of modern ML theory and outline interesting open questions that remain.

Double Descent and Other Interpolation Phenomena in GANs

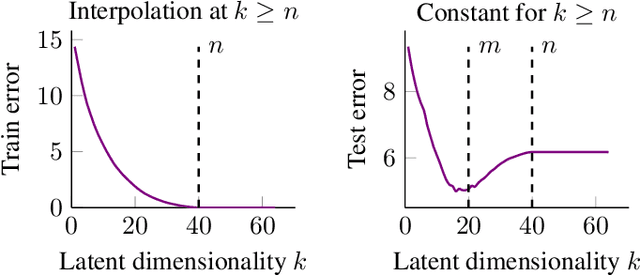
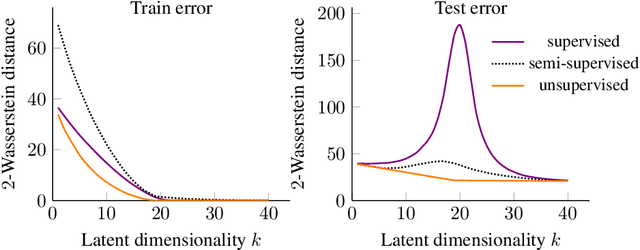
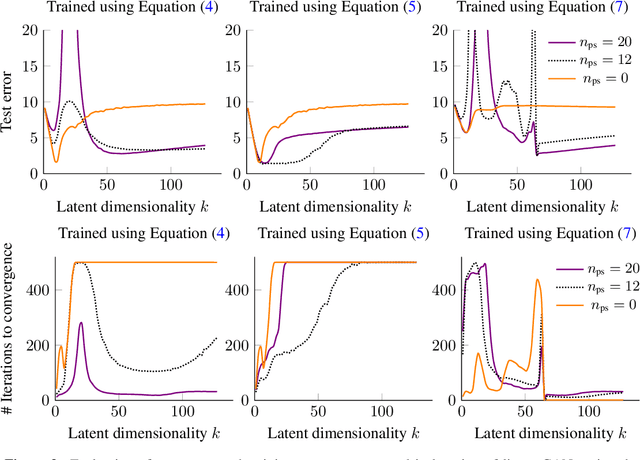
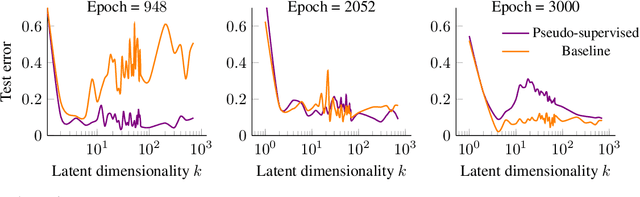
We study overparameterization in generative adversarial networks (GANs) that can interpolate the training data. We show that overparameterization can improve generalization performance and accelerate the training process. We study the generalization error as a function of latent space dimension and identify two main behaviors, depending on the learning setting. First, we show that overparameterized generative models that learn distributions by minimizing a metric or $f$-divergence do not exhibit double descent in generalization errors; specifically, all the interpolating solutions achieve the same generalization error. Second, we develop a new pseudo-supervised learning approach for GANs where the training utilizes pairs of fabricated (noise) inputs in conjunction with real output samples. Our pseudo-supervised setting exhibits double descent (and in some cases, triple descent) of generalization errors. We combine pseudo-supervision with overparameterization (i.e., overly large latent space dimension) to accelerate training while performing better, or close to, the generalization performance without pseudo-supervision. While our analysis focuses mostly on linear GANs, we also apply important insights for improving generalization of nonlinear, multilayer GANs.

Transfer Learning Can Outperform the True Prior in Double Descent Regularization

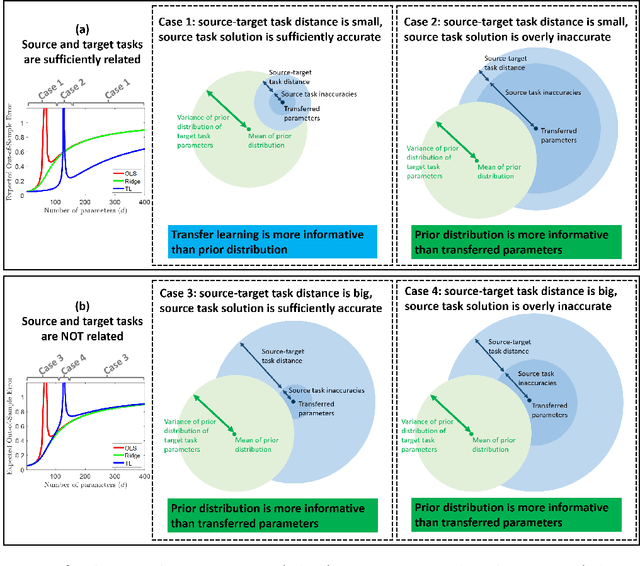
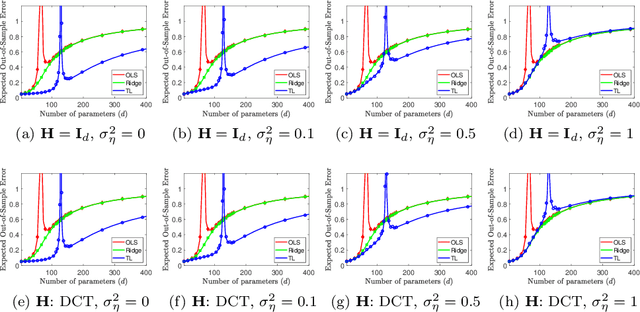
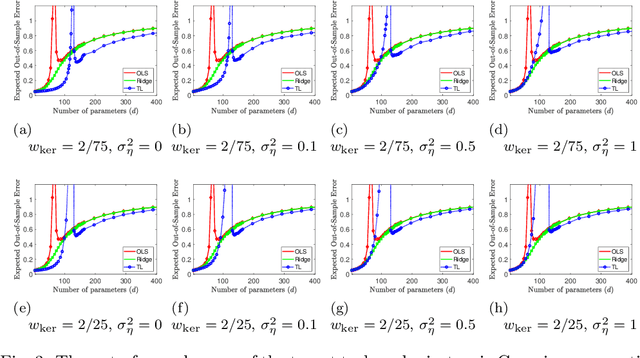
We study a fundamental transfer learning process from source to target linear regression tasks, including overparameterized settings where there are more learned parameters than data samples. The target task learning is addressed by using its training data together with the parameters previously computed for the source task. We define the target task as a linear regression optimization with a regularization on the distance between the to-be-learned target parameters and the already-learned source parameters. This approach can be also interpreted as adjusting the previously learned source parameters for the purpose of the target task, and in the case of sufficiently related tasks this process can be perceived as fine tuning. We analytically characterize the generalization performance of our transfer learning approach and demonstrate its ability to resolve the peak in generalization errors in double descent phenomena of min-norm solutions to ordinary least squares regression. Moreover, we show that for sufficiently related tasks the optimally tuned transfer learning approach can outperform the optimally tuned ridge regression method, even when the true parameter vector conforms with isotropic Gaussian prior distribution. Namely, we demonstrate that transfer learning can beat the minimum mean square error (MMSE) solution of the individual target task.

Regularized Compression of MRI Data: Modular Optimization of Joint Reconstruction and Coding

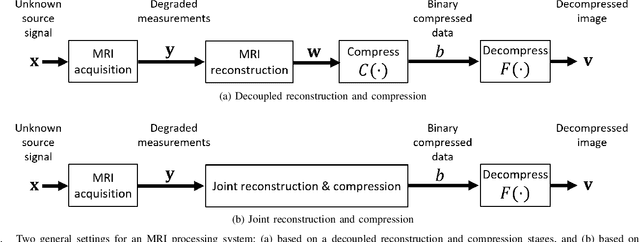
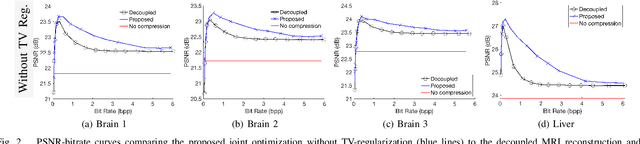
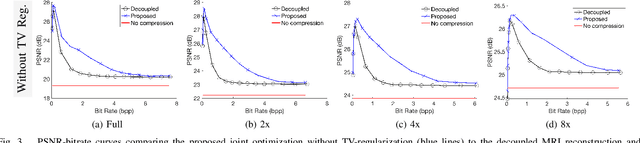
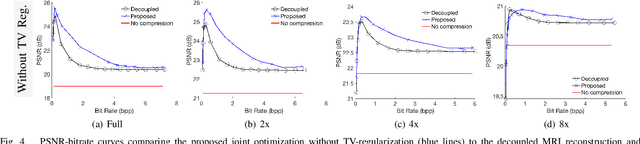
The Magnetic Resonance Imaging (MRI) processing chain starts with a critical acquisition stage that provides raw data for reconstruction of images for medical diagnosis. This flow usually includes a near-lossless data compression stage that enables digital storage and/or transmission in binary formats. In this work we propose a framework for joint optimization of the MRI reconstruction and lossy compression, producing compressed representations of medical images that achieve improved trade-offs between quality and bit-rate. Moreover, we demonstrate that lossy compression can even improve the reconstruction quality compared to settings based on lossless compression. Our method has a modular optimization structure, implemented using the alternating direction method of multipliers (ADMM) technique and the state-of-the-art image compression technique (BPG) as a black-box module iteratively applied. This establishes a medical data compression approach compatible with a lossy compression standard of choice. A main novelty of the proposed algorithm is in the total-variation regularization added to the modular compression process, leading to decompressed images of higher quality without any additional processing at/after the decompression stage. Our experiments show that our regularization-based approach for joint MRI reconstruction and compression often achieves significant PSNR gains between 4 to 9 dB at high bit-rates compared to non-regularized solutions of the joint task. Compared to regularization-based solutions, our optimization method provides PSNR gains between 0.5 to 1 dB at high bit-rates, which is the range of interest for medical image compression.