Just How Flexible are Neural Networks in Practice?

It is widely believed that a neural network can fit a training set containing at least as many samples as it has parameters, underpinning notions of overparameterized and underparameterized models. In practice, however, we only find solutions accessible via our training procedure, including the optimizer and regularizers, limiting flexibility. Moreover, the exact parameterization of the function class, built into an architecture, shapes its loss surface and impacts the minima we find. In this work, we examine the ability of neural networks to fit data in practice. Our findings indicate that: (1) standard optimizers find minima where the model can only fit training sets with significantly fewer samples than it has parameters; (2) convolutional networks are more parameter-efficient than MLPs and ViTs, even on randomly labeled data; (3) while stochastic training is thought to have a regularizing effect, SGD actually finds minima that fit more training data than full-batch gradient descent; (4) the difference in capacity to fit correctly labeled and incorrectly labeled samples can be predictive of generalization; (5) ReLU activation functions result in finding minima that fit more data despite being designed to avoid vanishing and exploding gradients in deep architectures.

Transformers Can Do Arithmetic with the Right Embeddings

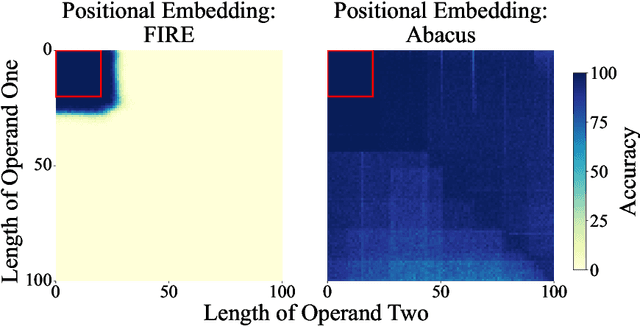
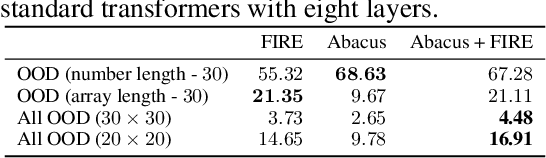
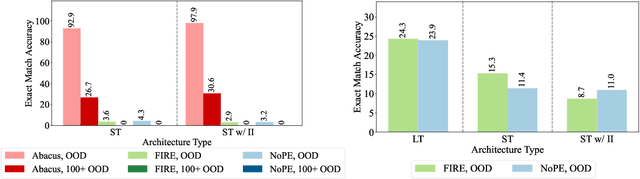
The poor performance of transformers on arithmetic tasks seems to stem in large part from their inability to keep track of the exact position of each digit inside of a large span of digits. We mend this problem by adding an embedding to each digit that encodes its position relative to the start of the number. In addition to the boost these embeddings provide on their own, we show that this fix enables architectural modifications such as input injection and recurrent layers to improve performance even further. With positions resolved, we can study the logical extrapolation ability of transformers. Can they solve arithmetic problems that are larger and more complex than those in their training data? We find that training on only 20 digit numbers with a single GPU for one day, we can reach state-of-the-art performance, achieving up to 99% accuracy on 100 digit addition problems. Finally, we show that these gains in numeracy also unlock improvements on other multi-step reasoning tasks including sorting and multiplication.

Generating Potent Poisons and Backdoors from Scratch with Guided Diffusion

Modern neural networks are often trained on massive datasets that are web scraped with minimal human inspection. As a result of this insecure curation pipeline, an adversary can poison or backdoor the resulting model by uploading malicious data to the internet and waiting for a victim to scrape and train on it. Existing approaches for creating poisons and backdoors start with randomly sampled clean data, called base samples, and then modify those samples to craft poisons. However, some base samples may be significantly more amenable to poisoning than others. As a result, we may be able to craft more potent poisons by carefully choosing the base samples. In this work, we use guided diffusion to synthesize base samples from scratch that lead to significantly more potent poisons and backdoors than previous state-of-the-art attacks. Our Guided Diffusion Poisoning (GDP) base samples can be combined with any downstream poisoning or backdoor attack to boost its effectiveness. Our implementation code is publicly available at: https://github.com/hsouri/GDP .

Universal Guidance for Diffusion Models

Typical diffusion models are trained to accept a particular form of conditioning, most commonly text, and cannot be conditioned on other modalities without retraining. In this work, we propose a universal guidance algorithm that enables diffusion models to be controlled by arbitrary guidance modalities without the need to retrain any use-specific components. We show that our algorithm successfully generates quality images with guidance functions including segmentation, face recognition, object detection, and classifier signals. Code is available at https://github.com/arpitbansal297/Universal-Guided-Diffusion.

Canary in a Coalmine: Better Membership Inference with Ensembled Adversarial Queries

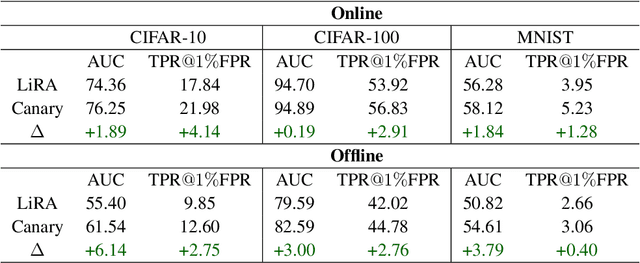
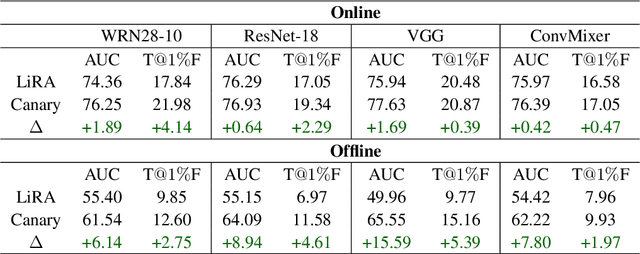
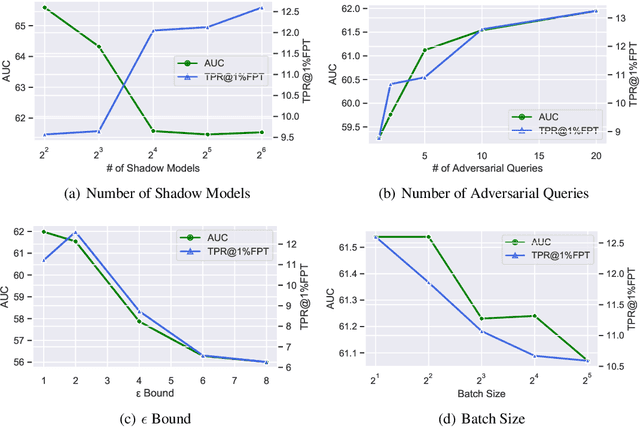
As industrial applications are increasingly automated by machine learning models, enforcing personal data ownership and intellectual property rights requires tracing training data back to their rightful owners. Membership inference algorithms approach this problem by using statistical techniques to discern whether a target sample was included in a model's training set. However, existing methods only utilize the unaltered target sample or simple augmentations of the target to compute statistics. Such a sparse sampling of the model's behavior carries little information, leading to poor inference capabilities. In this work, we use adversarial tools to directly optimize for queries that are discriminative and diverse. Our improvements achieve significantly more accurate membership inference than existing methods, especially in offline scenarios and in the low false-positive regime which is critical in legal settings. Code is available at https://github.com/YuxinWenRick/canary-in-a-coalmine.

Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise

Standard diffusion models involve an image transform -- adding Gaussian noise -- and an image restoration operator that inverts this degradation. We observe that the generative behavior of diffusion models is not strongly dependent on the choice of image degradation, and in fact an entire family of generative models can be constructed by varying this choice. Even when using completely deterministic degradations (e.g., blur, masking, and more), the training and test-time update rules that underlie diffusion models can be easily generalized to create generative models. The success of these fully deterministic models calls into question the community's understanding of diffusion models, which relies on noise in either gradient Langevin dynamics or variational inference, and paves the way for generalized diffusion models that invert arbitrary processes. Our code is available at https://github.com/arpitbansal297/Cold-Diffusion-Models

Certified Neural Network Watermarks with Randomized Smoothing

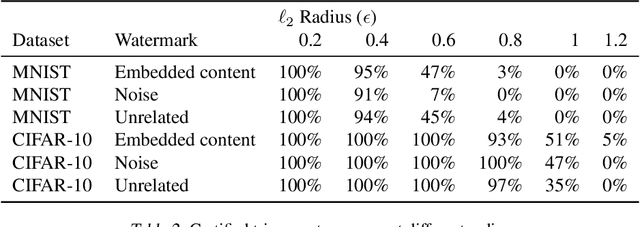
Watermarking is a commonly used strategy to protect creators' rights to digital images, videos and audio. Recently, watermarking methods have been extended to deep learning models -- in principle, the watermark should be preserved when an adversary tries to copy the model. However, in practice, watermarks can often be removed by an intelligent adversary. Several papers have proposed watermarking methods that claim to be empirically resistant to different types of removal attacks, but these new techniques often fail in the face of new or better-tuned adversaries. In this paper, we propose a certifiable watermarking method. Using the randomized smoothing technique proposed in Chiang et al., we show that our watermark is guaranteed to be unremovable unless the model parameters are changed by more than a certain l2 threshold. In addition to being certifiable, our watermark is also empirically more robust compared to previous watermarking methods. Our experiments can be reproduced with code at https://github.com/arpitbansal297/Certified_Watermarks

Transfer Learning with Deep Tabular Models

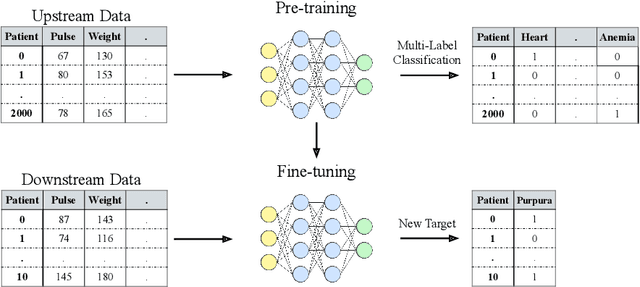
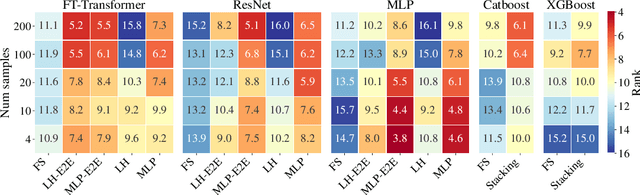
Recent work on deep learning for tabular data demonstrates the strong performance of deep tabular models, often bridging the gap between gradient boosted decision trees and neural networks. Accuracy aside, a major advantage of neural models is that they learn reusable features and are easily fine-tuned in new domains. This property is often exploited in computer vision and natural language applications, where transfer learning is indispensable when task-specific training data is scarce. In this work, we demonstrate that upstream data gives tabular neural networks a decisive advantage over widely used GBDT models. We propose a realistic medical diagnosis benchmark for tabular transfer learning, and we present a how-to guide for using upstream data to boost performance with a variety of tabular neural network architectures. Finally, we propose a pseudo-feature method for cases where the upstream and downstream feature sets differ, a tabular-specific problem widespread in real-world applications. Our code is available at https://github.com/LevinRoman/tabular-transfer-learning .

Can Neural Nets Learn the Same Model Twice? Investigating Reproducibility and Double Descent from the Decision Boundary Perspective

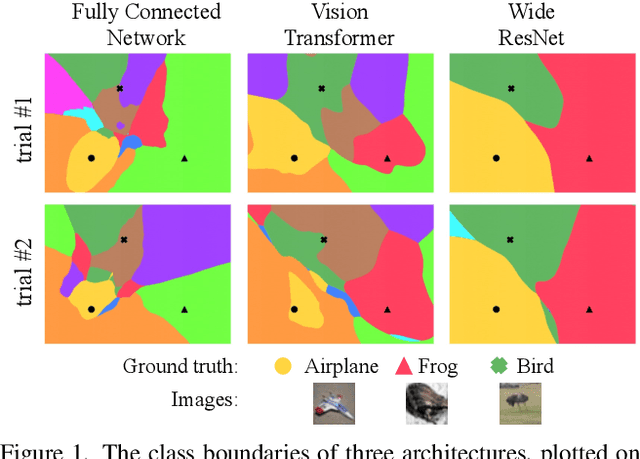
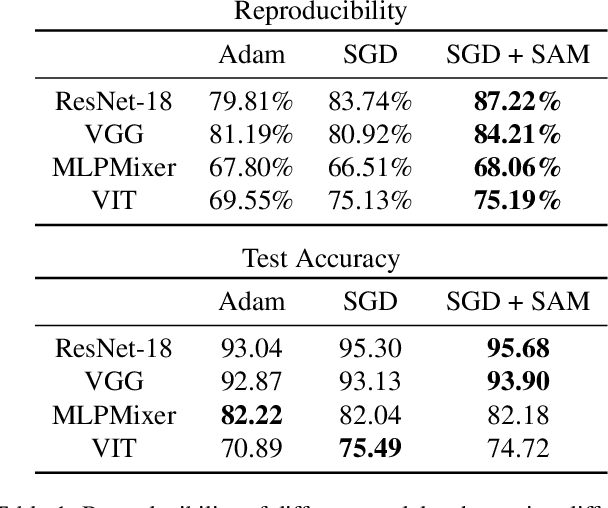
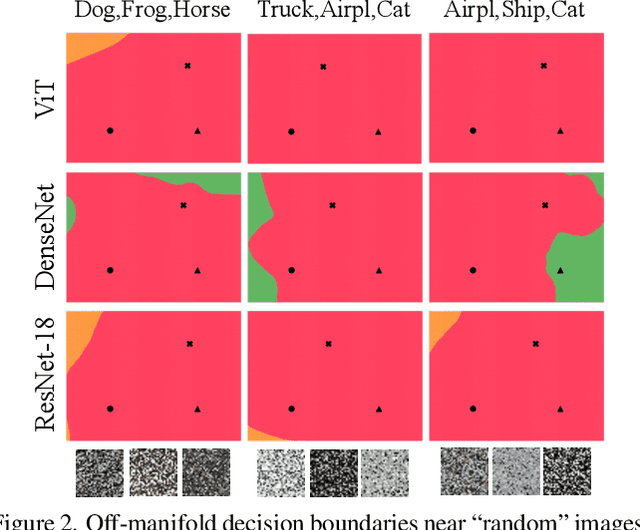
We discuss methods for visualizing neural network decision boundaries and decision regions. We use these visualizations to investigate issues related to reproducibility and generalization in neural network training. We observe that changes in model architecture (and its associate inductive bias) cause visible changes in decision boundaries, while multiple runs with the same architecture yield results with strong similarities, especially in the case of wide architectures. We also use decision boundary methods to visualize double descent phenomena. We see that decision boundary reproducibility depends strongly on model width. Near the threshold of interpolation, neural network decision boundaries become fragmented into many small decision regions, and these regions are non-reproducible. Meanwhile, very narrows and very wide networks have high levels of reproducibility in their decision boundaries with relatively few decision regions. We discuss how our observations relate to the theory of double descent phenomena in convex models. Code is available at https://github.com/somepago/dbViz

End-to-end Algorithm Synthesis with Recurrent Networks: Logical Extrapolation Without Overthinking

Machine learning systems perform well on pattern matching tasks, but their ability to perform algorithmic or logical reasoning is not well understood. One important reasoning capability is logical extrapolation, in which models trained only on small/simple reasoning problems can synthesize complex algorithms that scale up to large/complex problems at test time. Logical extrapolation can be achieved through recurrent systems, which can be iterated many times to solve difficult reasoning problems. We observe that this approach fails to scale to highly complex problems because behavior degenerates when many iterations are applied -- an issue we refer to as "overthinking." We propose a recall architecture that keeps an explicit copy of the problem instance in memory so that it cannot be forgotten. We also employ a progressive training routine that prevents the model from learning behaviors that are specific to iteration number and instead pushes it to learn behaviors that can be repeated indefinitely. These innovations prevent the overthinking problem, and enable recurrent systems to solve extremely hard logical extrapolation tasks, some requiring over 100K convolutional layers, without overthinking.