Large data limits and scaling laws for tSNE

This work considers large-data asymptotics for t-distributed stochastic neighbor embedding (tSNE), a widely-used non-linear dimension reduction algorithm. We identify an appropriate continuum limit of the tSNE objective function, which can be viewed as a combination of a kernel-based repulsion and an asymptotically-vanishing Laplacian-type regularizer. As a consequence, we show that embeddings of the original tSNE algorithm cannot have any consistent limit as $n \to \infty$. We propose a rescaled model which mitigates the asymptotic decay of the attractive energy, and which does have a consistent limit.

On Probabilistic Embeddings in Optimal Dimension Reduction

Dimension reduction algorithms are a crucial part of many data science pipelines, including data exploration, feature creation and selection, and denoising. Despite their wide utilization, many non-linear dimension reduction algorithms are poorly understood from a theoretical perspective. In this work we consider a generalized version of multidimensional scaling, which is posed as an optimization problem in which a mapping from a high-dimensional feature space to a lower-dimensional embedding space seeks to preserve either inner products or norms of the distribution in feature space, and which encompasses many commonly used dimension reduction algorithms. We analytically investigate the variational properties of this problem, leading to the following insights: 1) Solutions found using standard particle descent methods may lead to non-deterministic embeddings, 2) A relaxed or probabilistic formulation of the problem admits solutions with easily interpretable necessary conditions, 3) The globally optimal solutions to the relaxed problem actually must give a deterministic embedding. This progression of results mirrors the classical development of optimal transportation, and in a case relating to the Gromov-Wasserstein distance actually gives explicit insight into the structure of the optimal embeddings, which are parametrically determined and discontinuous. Finally, we illustrate that a standard computational implementation of this task does not learn deterministic embeddings, which means that it learns sub-optimal mappings, and that the embeddings learned in that context have highly misleading clustering structure, underscoring the delicate nature of solving this problem computationally.

Uniform Convergence of Adversarially Robust Classifiers

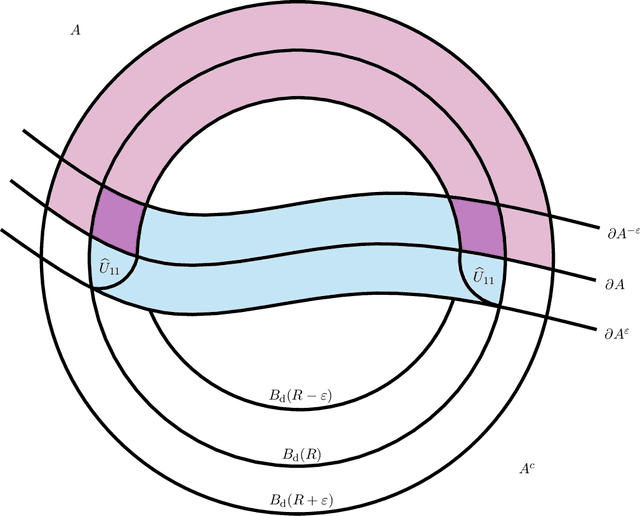
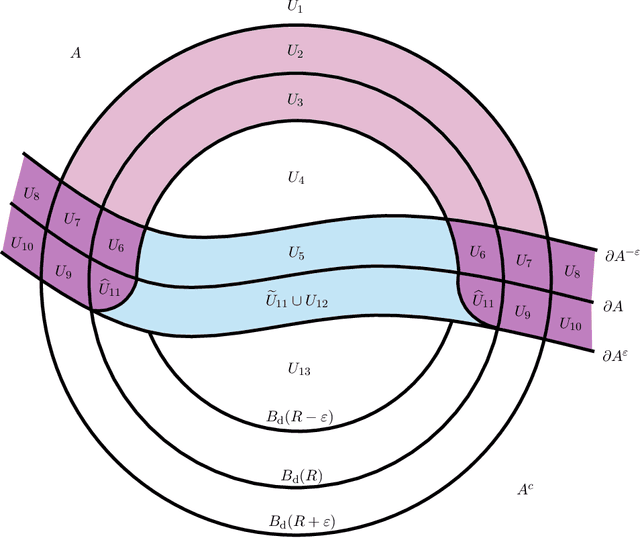
In recent years there has been significant interest in the effect of different types of adversarial perturbations in data classification problems. Many of these models incorporate the adversarial power, which is an important parameter with an associated trade-off between accuracy and robustness. This work considers a general framework for adversarially-perturbed classification problems, in a large data or population-level limit. In such a regime, we demonstrate that as adversarial strength goes to zero that optimal classifiers converge to the Bayes classifier in the Hausdorff distance. This significantly strengthens previous results, which generally focus on $L^1$-type convergence. The main argument relies upon direct geometric comparisons and is inspired by techniques from geometric measure theory.

Dirichlet Active Learning

This work introduces Dirichlet Active Learning (DiAL), a Bayesian-inspired approach to the design of active learning algorithms. Our framework models feature-conditional class probabilities as a Dirichlet random field and lends observational strength between similar features in order to calibrate the random field. This random field can then be utilized in learning tasks: in particular, we can use current estimates of mean and variance to conduct classification and active learning in the context where labeled data is scarce. We demonstrate the applicability of this model to low-label rate graph learning by constructing ``propagation operators'' based upon the graph Laplacian, and offer computational studies demonstrating the method's competitiveness with the state of the art. Finally, we provide rigorous guarantees regarding the ability of this approach to ensure both exploration and exploitation, expressed respectively in terms of cluster exploration and increased attention to decision boundaries.

Using Higher-Order Moments to Assess the Quality of GAN-generated Image Features

The rapid advancement of Generative Adversarial Networks (GANs) necessitates the need to robustly evaluate these models. Among the established evaluation criteria, the Fr\'{e}chet Inception Distance (FID) has been widely adopted due to its conceptual simplicity, fast computation time, and strong correlation with human perception. However, FID has inherent limitations, mainly stemming from its assumption that feature embeddings follow a Gaussian distribution, and therefore can be defined by their first two moments. As this does not hold in practice, in this paper we explore the importance of third-moments in image feature data and use this information to define a new measure, which we call the Skew Inception Distance (SID). We prove that SID is a pseudometric on probability distributions, show how it extends FID, and present a practical method for its computation. Our numerical experiments support that SID either tracks with FID or, in some cases, aligns more closely with human perception when evaluating image features of ImageNet data.

Rates of Convergence for Regression with the Graph Poly-Laplacian

In the (special) smoothing spline problem one considers a variational problem with a quadratic data fidelity penalty and Laplacian regularisation. Higher order regularity can be obtained via replacing the Laplacian regulariser with a poly-Laplacian regulariser. The methodology is readily adapted to graphs and here we consider graph poly-Laplacian regularisation in a fully supervised, non-parametric, noise corrupted, regression problem. In particular, given a dataset $\{x_i\}_{i=1}^n$ and a set of noisy labels $\{y_i\}_{i=1}^n\subset\mathbb{R}$ we let $u_n:\{x_i\}_{i=1}^n\to\mathbb{R}$ be the minimiser of an energy which consists of a data fidelity term and an appropriately scaled graph poly-Laplacian term. When $y_i = g(x_i)+\xi_i$, for iid noise $\xi_i$, and using the geometric random graph, we identify (with high probability) the rate of convergence of $u_n$ to $g$ in the large data limit $n\to\infty$. Furthermore, our rate, up to logarithms, coincides with the known rate of convergence in the usual smoothing spline model.

Eikonal depth: an optimal control approach to statistical depths

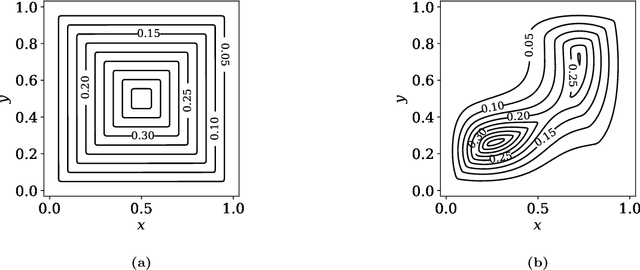
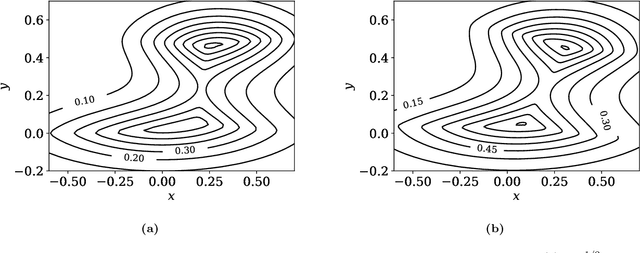
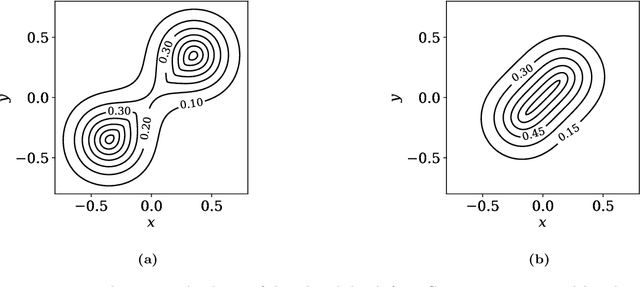
Statistical depths provide a fundamental generalization of quantiles and medians to data in higher dimensions. This paper proposes a new type of globally defined statistical depth, based upon control theory and eikonal equations, which measures the smallest amount of probability density that has to be passed through in a path to points outside the support of the distribution: for example spatial infinity. This depth is easy to interpret and compute, expressively captures multi-modal behavior, and extends naturally to data that is non-Euclidean. We prove various properties of this depth, and provide discussion of computational considerations. In particular, we demonstrate that this notion of depth is robust under an aproximate isometrically constrained adversarial model, a property which is not enjoyed by the Tukey depth. Finally we give some illustrative examples in the context of two-dimensional mixture models and MNIST.

The Geometry of Adversarial Training in Binary Classification

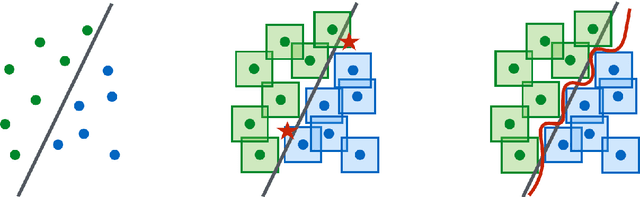
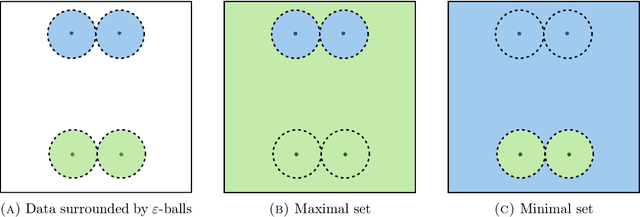
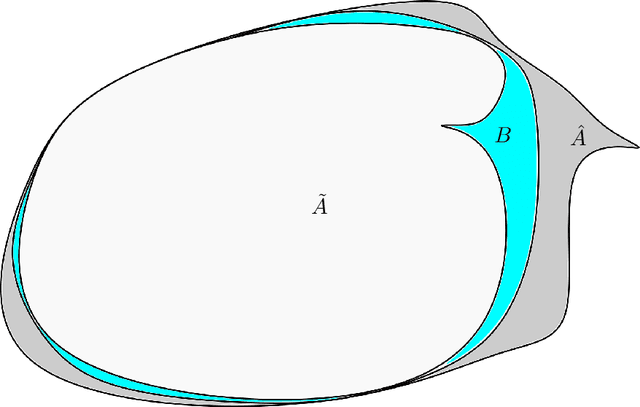
We establish an equivalence between a family of adversarial training problems for non-parametric binary classification and a family of regularized risk minimization problems where the regularizer is a nonlocal perimeter functional. The resulting regularized risk minimization problems admit exact convex relaxations of the type $L^1+$ (nonlocal) $\operatorname{TV}$, a form frequently studied in image analysis and graph-based learning. A rich geometric structure is revealed by this reformulation which in turn allows us to establish a series of properties of optimal solutions of the original problem, including the existence of minimal and maximal solutions (interpreted in a suitable sense), and the existence of regular solutions (also interpreted in a suitable sense). In addition, we highlight how the connection between adversarial training and perimeter minimization problems provides a novel, directly interpretable, statistical motivation for a family of regularized risk minimization problems involving perimeter/total variation. The majority of our theoretical results are independent of the distance used to define adversarial attacks.

Tukey Depths and Hamilton-Jacobi Differential Equations

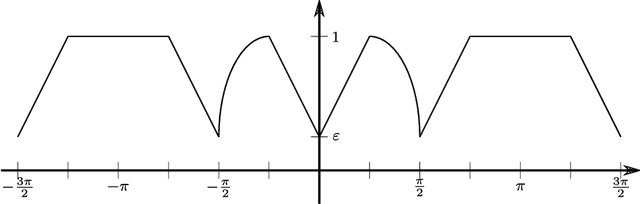
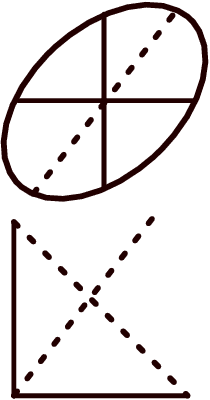
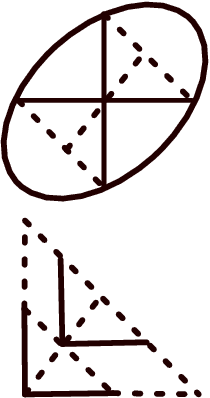
The widespread application of modern machine learning has increased the need for robust statistical algorithms. This work studies one such fundamental statistical measure known as the Tukey depth. We study the problem in the continuum (population) limit. In particular, we derive the associated necessary conditions, which take the form of a first-order partial differential equation. We discuss the classical interpretation of this necessary condition as the viscosity solution of a Hamilton-Jacobi equation, but with a non-classical Hamiltonian with discontinuous dependence on the gradient at zero. We prove that this equation possesses a unique viscosity solution and that this solution always bounds the Tukey depth from below. In certain cases, we prove that the Tukey depth is equal to the viscosity solution, and we give some illustrations of standard numerical methods from the optimal control community which deal directly with the partial differential equation. We conclude by outlining several promising research directions both in terms of new numerical algorithms and theoretical challenges.

Adversarial Classification: Necessary conditions and geometric flows

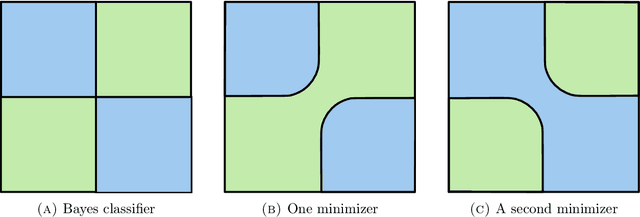
We study a version of adversarial classification where an adversary is empowered to corrupt data inputs up to some distance $\varepsilon$, using tools from variational analysis. In particular, we describe necessary conditions associated with the optimal classifier subject to such an adversary. Using the necessary conditions, we derive a geometric evolution equation which can be used to track the change in classification boundaries as $\varepsilon$ varies. This evolution equation may be described as an uncoupled system of differential equations in one dimension, or as a mean curvature type equation in higher dimension. In one dimension we rigorously prove that one can use the initial value problem starting from $\varepsilon=0$, which is simply the Bayes classifier, in order to solve for the global minimizer of the adversarial problem. Numerical examples illustrating these ideas are also presented.