Sparse Training of Neural Networks based on Multilevel Mirror Descent

We introduce a dynamic sparse training algorithm based on linearized Bregman iterations / mirror descent that exploits the naturally incurred sparsity by alternating between periods of static and dynamic sparsity pattern updates. The key idea is to combine sparsity-inducing Bregman iterations with adaptive freezing of the network structure to enable efficient exploration of the sparse parameter space while maintaining sparsity. We provide convergence guaranties by embedding our method in a multilevel optimization framework. Furthermore, we empirically show that our algorithm can produce highly sparse and accurate models on standard benchmarks. We also show that the theoretical number of FLOPs compared to SGD training can be reduced from 38% for standard Bregman iterations to 6% for our method while maintaining test accuracy.

Meshless Shape Optimization using Neural Networks and Partial Differential Equations on Graphs

Shape optimization involves the minimization of a cost function defined over a set of shapes, often governed by a partial differential equation (PDE). In the absence of closed-form solutions, one relies on numerical methods to approximate the solution. The level set method -- when coupled with the finite element method -- is one of the most versatile numerical shape optimization approaches but still suffers from the limitations of most mesh-based methods. In this work, we present a fully meshless level set framework that leverages neural networks to parameterize the level set function and employs the graph Laplacian to approximate the underlying PDE. Our approach enables precise computations of geometric quantities such as surface normals and curvature, and allows tackling optimization problems within the class of convex shapes.

MirrorCBO: A consensus-based optimization method in the spirit of mirror descent

In this work we propose MirrorCBO, a consensus-based optimization (CBO) method which generalizes standard CBO in the same way that mirror descent generalizes gradient descent. For this we apply the CBO methodology to a swarm of dual particles and retain the primal particle positions by applying the inverse of the mirror map, which we parametrize as the subdifferential of a strongly convex function $\phi$. In this way, we combine the advantages of a derivative-free non-convex optimization algorithm with those of mirror descent. As a special case, the method extends CBO to optimization problems with convex constraints. Assuming bounds on the Bregman distance associated to $\phi$, we provide asymptotic convergence results for MirrorCBO with explicit exponential rate. Another key contribution is an exploratory numerical study of this new algorithm across different application settings, focusing on (i) sparsity-inducing optimization, and (ii) constrained optimization, demonstrating the competitive performance of MirrorCBO. We observe empirically that the method can also be used for optimization on (non-convex) submanifolds of Euclidean space, can be adapted to mirrored versions of other recent CBO variants, and that it inherits from mirror descent the capability to select desirable minimizers, like sparse ones. We also include an overview of recent CBO approaches for constrained optimization and compare their performance to MirrorCBO.

Convergence rates for Poisson learning to a Poisson equation with measure data

In this paper we prove discrete to continuum convergence rates for Poisson Learning, a graph-based semi-supervised learning algorithm that is based on solving the graph Poisson equation with a source term consisting of a linear combination of Dirac deltas located at labeled points and carrying label information. The corresponding continuum equation is a Poisson equation with measure data in a Euclidean domain $\Omega \subset \mathbb{R}^d$. The singular nature of these equations is challenging and requires an approach with several distinct parts: (1) We prove quantitative error estimates when convolving the measure data of a Poisson equation with (approximately) radial function supported on balls. (2) We use quantitative variational techniques to prove discrete to continuum convergence rates on random geometric graphs with bandwidth $\varepsilon>0$ for bounded source terms. (3) We show how to regularize the graph Poisson equation via mollification with the graph heat kernel, and we study fine asymptotics of the heat kernel on random geometric graphs. Combining these three pillars we obtain $L^1$ convergence rates that scale, up to logarithmic factors, like $O(\varepsilon^{\frac{1}{d+2}})$ for general data distributions, and $O(\varepsilon^{\frac{2-\sigma}{d+4}})$ for uniformly distributed data, where $\sigma>0$. These rates are valid with high probability if $\varepsilon\gg\left({\log n}/{n}\right)^q$ where $n$ denotes the number of vertices of the graph and $q \approx \frac{1}{3d}$.

A mean curvature flow arising in adversarial training

We connect adversarial training for binary classification to a geometric evolution equation for the decision boundary. Relying on a perspective that recasts adversarial training as a regularization problem, we introduce a modified training scheme that constitutes a minimizing movements scheme for a nonlocal perimeter functional. We prove that the scheme is monotone and consistent as the adversarial budget vanishes and the perimeter localizes, and as a consequence we rigorously show that the scheme approximates a weighted mean curvature flow. This highlights that the efficacy of adversarial training may be due to locally minimizing the length of the decision boundary. In our analysis, we introduce a variety of tools for working with the subdifferential of a supremal-type nonlocal total variation and its regularity properties.

It begins with a boundary: A geometric view on probabilistically robust learning

Although deep neural networks have achieved super-human performance on many classification tasks, they often exhibit a worrying lack of robustness towards adversarially generated examples. Thus, considerable effort has been invested into reformulating Empirical Risk Minimization (ERM) into an adversarially robust framework. Recently, attention has shifted towards approaches which interpolate between the robustness offered by adversarial training and the higher clean accuracy and faster training times of ERM. In this paper, we take a fresh and geometric view on one such method -- Probabilistically Robust Learning (PRL) (Robey et al., ICML, 2022). We propose a geometric framework for understanding PRL, which allows us to identify a subtle flaw in its original formulation and to introduce a family of probabilistic nonlocal perimeter functionals to address this. We prove existence of solutions using novel relaxation methods and study properties as well as local limits of the introduced perimeters.

Gamma-convergence of a nonlocal perimeter arising in adversarial machine learning

In this paper we prove Gamma-convergence of a nonlocal perimeter of Minkowski type to a local anisotropic perimeter. The nonlocal model describes the regularizing effect of adversarial training in binary classifications. The energy essentially depends on the interaction between two distributions modelling likelihoods for the associated classes. We overcome typical strict regularity assumptions for the distributions by only assuming that they have bounded $BV$ densities. In the natural topology coming from compactness, we prove Gamma-convergence to a weighted perimeter with weight determined by an anisotropic function of the two densities. Despite being local, this sharp interface limit reflects classification stability with respect to adversarial perturbations. We further apply our results to deduce Gamma-convergence of the associated total variations, to study the asymptotics of adversarial training, and to prove Gamma-convergence of graph discretizations for the nonlocal perimeter.

Improving Robustness against Real-World and Worst-Case Distribution Shifts through Decision Region Quantification

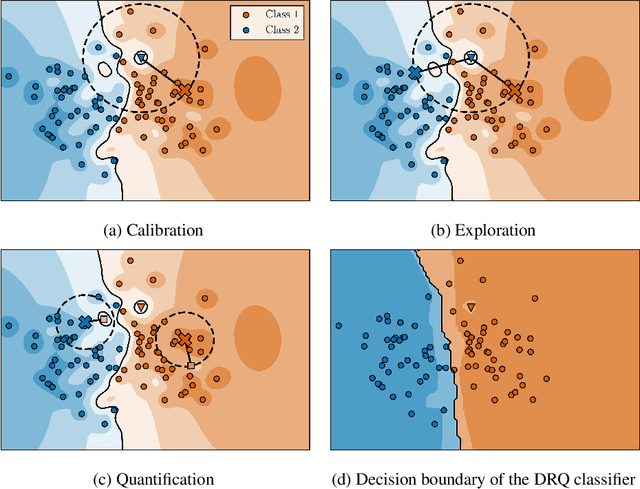
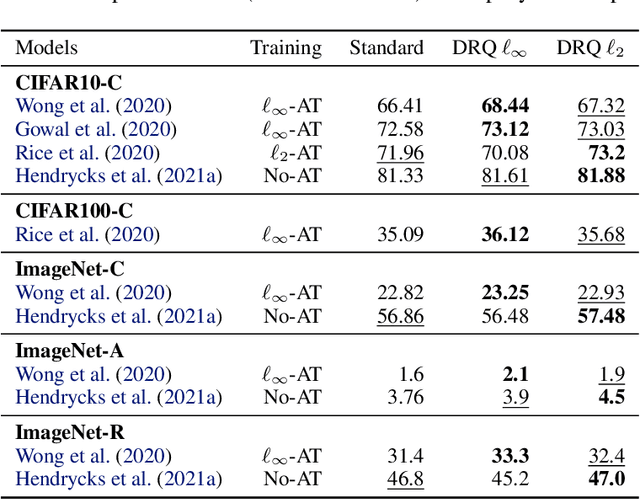
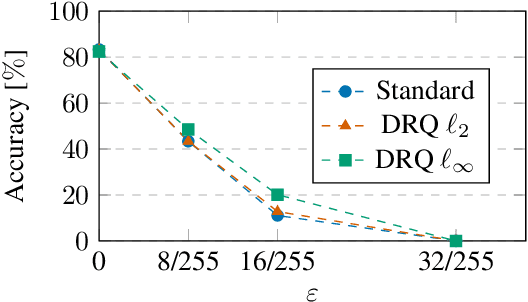
The reliability of neural networks is essential for their use in safety-critical applications. Existing approaches generally aim at improving the robustness of neural networks to either real-world distribution shifts (e.g., common corruptions and perturbations, spatial transformations, and natural adversarial examples) or worst-case distribution shifts (e.g., optimized adversarial examples). In this work, we propose the Decision Region Quantification (DRQ) algorithm to improve the robustness of any differentiable pre-trained model against both real-world and worst-case distribution shifts in the data. DRQ analyzes the robustness of local decision regions in the vicinity of a given data point to make more reliable predictions. We theoretically motivate the DRQ algorithm by showing that it effectively smooths spurious local extrema in the decision surface. Furthermore, we propose an implementation using targeted and untargeted adversarial attacks. An extensive empirical evaluation shows that DRQ increases the robustness of adversarially and non-adversarially trained models against real-world and worst-case distribution shifts on several computer vision benchmark datasets.

The Geometry of Adversarial Training in Binary Classification

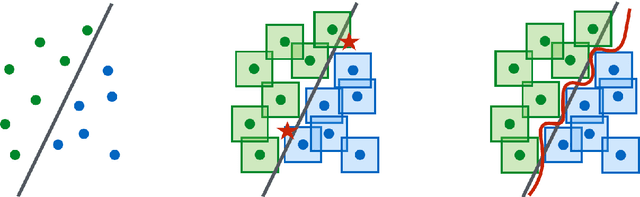
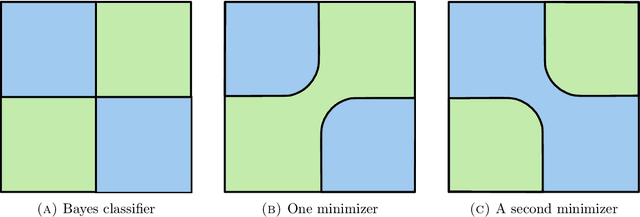
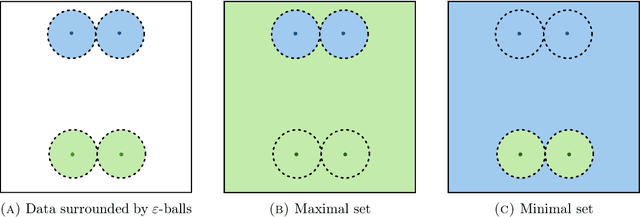
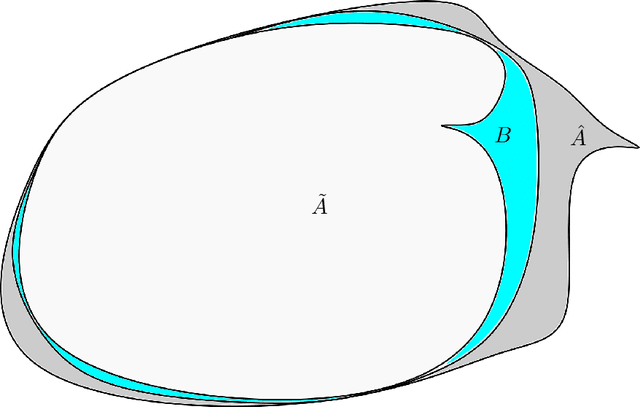
We establish an equivalence between a family of adversarial training problems for non-parametric binary classification and a family of regularized risk minimization problems where the regularizer is a nonlocal perimeter functional. The resulting regularized risk minimization problems admit exact convex relaxations of the type $L^1+$ (nonlocal) $\operatorname{TV}$, a form frequently studied in image analysis and graph-based learning. A rich geometric structure is revealed by this reformulation which in turn allows us to establish a series of properties of optimal solutions of the original problem, including the existence of minimal and maximal solutions (interpreted in a suitable sense), and the existence of regular solutions (also interpreted in a suitable sense). In addition, we highlight how the connection between adversarial training and perimeter minimization problems provides a novel, directly interpretable, statistical motivation for a family of regularized risk minimization problems involving perimeter/total variation. The majority of our theoretical results are independent of the distance used to define adversarial attacks.

Uniform Convergence Rates for Lipschitz Learning on Graphs

Lipschitz learning is a graph-based semi-supervised learning method where one extends labels from a labeled to an unlabeled data set by solving the infinity Laplace equation on a weighted graph. In this work we prove uniform convergence rates for solutions of the graph infinity Laplace equation as the number of vertices grows to infinity. Their continuum limits are absolutely minimizing Lipschitz extensions with respect to the geodesic metric of the domain where the graph vertices are sampled from. We work under very general assumptions on the graph weights, the set of labeled vertices, and the continuum domain. Our main contribution is that we obtain quantitative convergence rates even for very sparsely connected graphs, as they typically appear in applications like semi-supervised learning. In particular, our framework allows for graph bandwidths down to the connectivity radius. For proving this we first show a quantitative convergence statement for graph distance functions to geodesic distance functions in the continuum. Using the "comparison with distance functions" principle, we can pass these convergence statements to infinity harmonic functions and absolutely minimizing Lipschitz extensions.