A Tunable Despeckling Neural Network Stabilized via Diffusion Equation

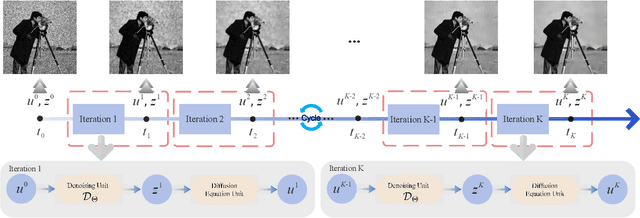
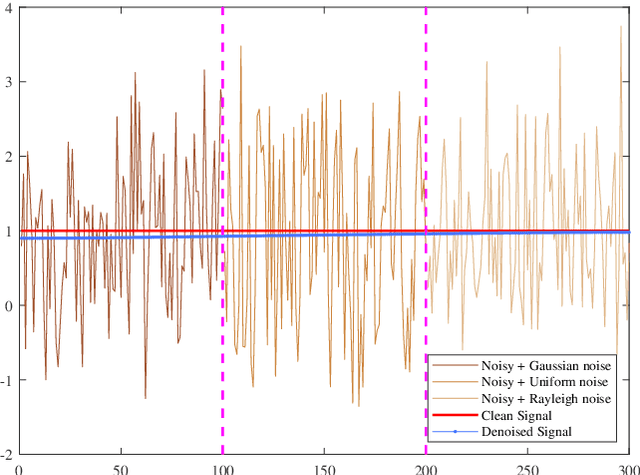
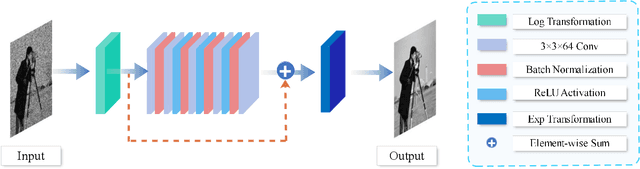
Multiplicative Gamma noise remove is a critical research area in the application of synthetic aperture radar (SAR) imaging, where neural networks serve as a potent tool. However, real-world data often diverges from theoretical models, exhibiting various disturbances, which makes the neural network less effective. Adversarial attacks work by finding perturbations that significantly disrupt functionality of neural networks, as the inherent instability of neural networks makes them highly susceptible. A network designed to withstand such extreme cases can more effectively mitigate general disturbances in real SAR data. In this work, the dissipative nature of diffusion equations is employed to underpin a novel approach for countering adversarial attacks and improve the resistance of real noise disturbance. We propose a tunable, regularized neural network that unrolls a denoising unit and a regularization unit into a single network for end-to-end training. In the network, the denoising unit and the regularization unit are composed of the denoising network and the simplest linear diffusion equation respectively. The regularization unit enhances network stability, allowing post-training time step adjustments to effectively mitigate the adverse impacts of adversarial attacks. The stability and convergence of our model are theoretically proven, and in the experiments, we compare our model with several state-of-the-art denoising methods on simulated images, adversarial samples, and real SAR images, yielding superior results in both quantitative and visual evaluations.

Hypergraph $p$-Laplacian equations for data interpolation and semi-supervised learning

Hypergraph learning with $p$-Laplacian regularization has attracted a lot of attention due to its flexibility in modeling higher-order relationships in data. This paper focuses on its fast numerical implementation, which is challenging due to the non-differentiability of the objective function and the non-uniqueness of the minimizer. We derive a hypergraph $p$-Laplacian equation from the subdifferential of the $p$-Laplacian regularization. A simplified equation that is mathematically well-posed and computationally efficient is proposed as an alternative. Numerical experiments verify that the simplified $p$-Laplacian equation suppresses spiky solutions in data interpolation and improves classification accuracy in semi-supervised learning. The remarkably low computational cost enables further applications.

Adversarial flows: A gradient flow characterization of adversarial attacks

A popular method to perform adversarial attacks on neuronal networks is the so-called fast gradient sign method and its iterative variant. In this paper, we interpret this method as an explicit Euler discretization of a differential inclusion, where we also show convergence of the discretization to the associated gradient flow. To do so, we consider the concept of p-curves of maximal slope in the case $p=\infty$. We prove existence of $\infty$-curves of maximum slope and derive an alternative characterization via differential inclusions. Furthermore, we also consider Wasserstein gradient flows for potential energies, where we show that curves in the Wasserstein space can be characterized by a representing measure on the space of curves in the underlying Banach space, which fulfill the differential inclusion. The application of our theory to the finite-dimensional setting is twofold: On the one hand, we show that a whole class of normalized gradient descent methods (in particular signed gradient descent) converge, up to subsequences, to the flow, when sending the step size to zero. On the other hand, in the distributional setting, we show that the inner optimization task of adversarial training objective can be characterized via $\infty$-curves of maximum slope on an appropriate optimal transport space.

Hypergraph $p$-Laplacian regularization on point clouds for data interpolation

As a generalization of graphs, hypergraphs are widely used to model higher-order relations in data. This paper explores the benefit of the hypergraph structure for the interpolation of point cloud data that contain no explicit structural information. We define the $\varepsilon_n$-ball hypergraph and the $k_n$-nearest neighbor hypergraph on a point cloud and study the $p$-Laplacian regularization on the hypergraphs. We prove the variational consistency between the hypergraph $p$-Laplacian regularization and the continuum $p$-Laplacian regularization in a semisupervised setting when the number of points $n$ goes to infinity while the number of labeled points remains fixed. A key improvement compared to the graph case is that the results rely on weaker assumptions on the upper bound of $\varepsilon_n$ and $k_n$. To solve the convex but non-differentiable large-scale optimization problem, we utilize the stochastic primal-dual hybrid gradient algorithm. Numerical experiments on data interpolation verify that the hypergraph $p$-Laplacian regularization outperforms the graph $p$-Laplacian regularization in preventing the development of spikes at the labeled points.

Continuum limit of $p$-biharmonic equations on graphs

This paper studies the $p$-biharmonic equation on graphs, which arises in point cloud processing and can be interpreted as a natural extension of the graph $p$-Laplacian from the perspective of hypergraph. The asymptotic behavior of the solution is investigated when the random geometric graph is considered and the number of data points goes to infinity. We show that the continuum limit is an appropriately weighted $p$-biharmonic equation with homogeneous Neumann boundary conditions. The result relies on the uniform $L^p$ estimates for solutions and gradients of nonlocal and graph Poisson equations. The $L^\infty$ estimates of solutions are also obtained as a byproduct.

Learned Regularization for Inverse Problems: Insights from a Spectral Model

The aim of this paper is to provide a theoretically founded investigation of state-of-the-art learning approaches for inverse problems. We give an extended definition of regularization methods and their convergence in terms of the underlying data distributions, which paves the way for future theoretical studies. Based on a simple spectral learning model previously introduced for supervised learning, we investigate some key properties of different learning paradigms for inverse problems, which can be formulated independently of specific architectures. In particular we investigate the regularization properties, bias, and critical dependence on training data distributions. Moreover, our framework allows to highlight and compare the specific behavior of the different paradigms in the infinite-dimensional limit.

Learning a Sparse Representation of Barron Functions with the Inverse Scale Space Flow

This paper presents a method for finding a sparse representation of Barron functions. Specifically, given an $L^2$ function $f$, the inverse scale space flow is used to find a sparse measure $\mu$ minimising the $L^2$ loss between the Barron function associated to the measure $\mu$ and the function $f$. The convergence properties of this method are analysed in an ideal setting and in the cases of measurement noise and sampling bias. In an ideal setting the objective decreases strictly monotone in time to a minimizer with $\mathcal{O}(1/t)$, and in the case of measurement noise or sampling bias the optimum is achieved up to a multiplicative or additive constant. This convergence is preserved on discretization of the parameter space, and the minimizers on increasingly fine discretizations converge to the optimum on the full parameter space.

Resolution-Invariant Image Classification based on Fourier Neural Operators

In this paper we investigate the use of Fourier Neural Operators (FNOs) for image classification in comparison to standard Convolutional Neural Networks (CNNs). Neural operators are a discretization-invariant generalization of neural networks to approximate operators between infinite dimensional function spaces. FNOs - which are neural operators with a specific parametrization - have been applied successfully in the context of parametric PDEs. We derive the FNO architecture as an example for continuous and Fr\'echet-differentiable neural operators on Lebesgue spaces. We further show how CNNs can be converted into FNOs and vice versa and propose an interpolation-equivariant adaptation of the architecture.

Convergent Data-driven Regularizations for CT Reconstruction

The reconstruction of images from their corresponding noisy Radon transform is a typical example of an ill-posed linear inverse problem as arising in the application of computerized tomography (CT). As the (na\"{\i}ve) solution does not depend on the measured data continuously, regularization is needed to re-establish a continuous dependence. In this work, we investigate simple, but yet still provably convergent approaches to learning linear regularization methods from data. More specifically, we analyze two approaches: One generic linear regularization that learns how to manipulate the singular values of the linear operator in an extension of [1], and one tailored approach in the Fourier domain that is specific to CT-reconstruction. We prove that such approaches become convergent regularization methods as well as the fact that the reconstructions they provide are typically much smoother than the training data they were trained on. Finally, we compare the spectral as well as the Fourier-based approaches for CT-reconstruction numerically, discuss their advantages and disadvantages and investigate the effect of discretization errors at different resolutions.

Analysis of Kinetic Models for Label Switching and Stochastic Gradient Descent

In this paper we provide a novel approach to the analysis of kinetic models for label switching, which are used for particle systems that can randomly switch between gradient flows in different energy landscapes. Besides problems in biology and physics, we also demonstrate that stochastic gradient descent, the most popular technique in machine learning, can be understood in this setting, when considering a time-continuous variant. Our analysis is focusing on the case of evolution in a collection of external potentials, for which we provide analytical and numerical results about the evolution as well as the stationary problem.