Resolution-Invariant Image Classification based on Fourier Neural Operators

In this paper we investigate the use of Fourier Neural Operators (FNOs) for image classification in comparison to standard Convolutional Neural Networks (CNNs). Neural operators are a discretization-invariant generalization of neural networks to approximate operators between infinite dimensional function spaces. FNOs - which are neural operators with a specific parametrization - have been applied successfully in the context of parametric PDEs. We derive the FNO architecture as an example for continuous and Fr\'echet-differentiable neural operators on Lebesgue spaces. We further show how CNNs can be converted into FNOs and vice versa and propose an interpolation-equivariant adaptation of the architecture.

Neural Architecture Search via Bregman Iterations

We propose a novel strategy for Neural Architecture Search (NAS) based on Bregman iterations. Starting from a sparse neural network our gradient-based one-shot algorithm gradually adds relevant parameters in an inverse scale space manner. This allows the network to choose the best architecture in the search space which makes it well-designed for a given task, e.g., by adding neurons or skip connections. We demonstrate that using our approach one can unveil, for instance, residual autoencoders for denoising, deblurring, and classification tasks. Code is available at https://github.com/TimRoith/BregmanLearning.

A Bregman Learning Framework for Sparse Neural Networks

We propose a learning framework based on stochastic Bregman iterations to train sparse neural networks with an inverse scale space approach. We derive a baseline algorithm called LinBreg, an accelerated version using momentum, and AdaBreg, which is a Bregmanized generalization of the Adam algorithm. In contrast to established methods for sparse training the proposed family of algorithms constitutes a regrowth strategy for neural networks that is solely optimization-based without additional heuristics. Our Bregman learning framework starts the training with very few initial parameters, successively adding only significant ones to obtain a sparse and expressive network. The proposed approach is extremely easy and efficient, yet supported by the rich mathematical theory of inverse scale space methods. We derive a statistically profound sparse parameter initialization strategy and provide a rigorous stochastic convergence analysis of the loss decay and additional convergence proofs in the convex regime. Using only 3.4% of the parameters of ResNet-18 we achieve 90.2% test accuracy on CIFAR-10, compared to 93.6% using the dense network. Our algorithm also unveils an autoencoder architecture for a denoising task. The proposed framework also has a huge potential for integrating sparse backpropagation and resource-friendly training.

CLIP: Cheap Lipschitz Training of Neural Networks

Despite the large success of deep neural networks (DNN) in recent years, most neural networks still lack mathematical guarantees in terms of stability. For instance, DNNs are vulnerable to small or even imperceptible input perturbations, so called adversarial examples, that can cause false predictions. This instability can have severe consequences in applications which influence the health and safety of humans, e.g., biomedical imaging or autonomous driving. While bounding the Lipschitz constant of a neural network improves stability, most methods rely on restricting the Lipschitz constants of each layer which gives a poor bound for the actual Lipschitz constant. In this paper we investigate a variational regularization method named CLIP for controlling the Lipschitz constant of a neural network, which can easily be integrated into the training procedure. We mathematically analyze the proposed model, in particular discussing the impact of the chosen regularization parameter on the output of the network. Finally, we numerically evaluate our method on both a nonlinear regression problem and the MNIST and Fashion-MNIST classification databases, and compare our results with a weight regularization approach.

Identifying Untrustworthy Predictions in Neural Networks by Geometric Gradient Analysis

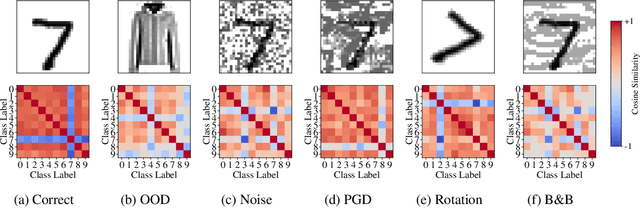
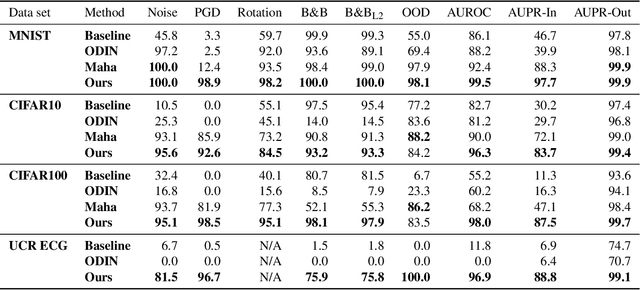
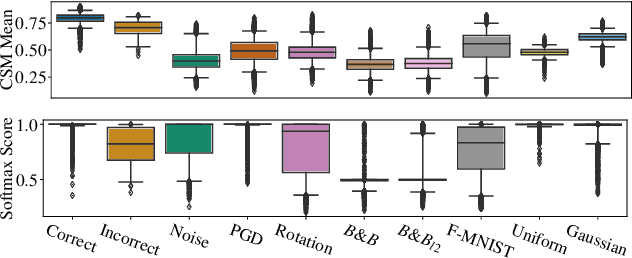
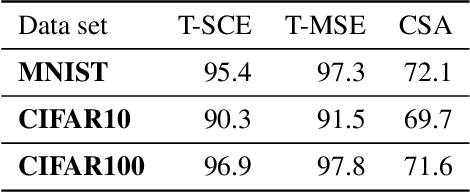
The susceptibility of deep neural networks to untrustworthy predictions, including out-of-distribution (OOD) data and adversarial examples, still prevent their widespread use in safety-critical applications. Most existing methods either require a re-training of a given model to achieve robust identification of adversarial attacks or are limited to out-of-distribution sample detection only. In this work, we propose a geometric gradient analysis (GGA) to improve the identification of untrustworthy predictions without retraining of a given model. GGA analyzes the geometry of the loss landscape of neural networks based on the saliency maps of their respective input. To motivate the proposed approach, we provide theoretical connections between gradients' geometrical properties and local minima of the loss function. Furthermore, we demonstrate that the proposed method outperforms prior approaches in detecting OOD data and adversarial attacks, including state-of-the-art and adaptive attacks.

Sampled Nonlocal Gradients for Stronger Adversarial Attacks

The vulnerability of deep neural networks to small and even imperceptible perturbations has become a central topic in deep learning research. The evaluation of new defense mechanisms for these so-called adversarial attacks has proven to be challenging. Although several sophisticated defense mechanisms were introduced, most of them were later shown to be ineffective. However, a reliable evaluation of model robustness is mandatory for deployment in safety-critical real-world scenarios. We propose a simple yet effective modification to the gradient calculation of state-of-the-art first-order adversarial attacks, which increases their success rate and thus leads to more accurate robustness estimates. Normally, the gradient update of an attack is directly calculated for the given data point. In general, this approach is sensitive to noise and small local optima of the loss function. Inspired by gradient sampling techniques from non-convex optimization, we propose to calculate the gradient direction of the adversarial attack as the weighted average over multiple points in the local vicinity. We empirically show that by incorporating this additional gradient information, we are able to give a more accurate estimation of the global descent direction on noisy and non-convex loss surfaces. Additionally, we show that the proposed method achieves higher success rates than a variety of state-of-the-art attacks on the benchmark datasets MNIST, Fashion-MNIST, and CIFAR10.

Computing Nonlinear Eigenfunctions via Gradient Flow Extinction

In this work we investigate the computation of nonlinear eigenfunctions via the extinction profiles of gradient flows. We analyze a scheme that recursively subtracts such eigenfunctions from given data and show that this procedure yields a decomposition of the data into eigenfunctions in some cases as the 1-dimensional total variation, for instance. We discuss results of numerical experiments in which we use extinction profiles and the gradient flow for the task of spectral graph clustering as used, e.g., in machine learning applications.