Convergent Data-driven Regularizations for CT Reconstruction

The reconstruction of images from their corresponding noisy Radon transform is a typical example of an ill-posed linear inverse problem as arising in the application of computerized tomography (CT). As the (na\"{\i}ve) solution does not depend on the measured data continuously, regularization is needed to re-establish a continuous dependence. In this work, we investigate simple, but yet still provably convergent approaches to learning linear regularization methods from data. More specifically, we analyze two approaches: One generic linear regularization that learns how to manipulate the singular values of the linear operator in an extension of [1], and one tailored approach in the Fourier domain that is specific to CT-reconstruction. We prove that such approaches become convergent regularization methods as well as the fact that the reconstructions they provide are typically much smoother than the training data they were trained on. Finally, we compare the spectral as well as the Fourier-based approaches for CT-reconstruction numerically, discuss their advantages and disadvantages and investigate the effect of discretization errors at different resolutions.

Lifting the Convex Conjugate in Lagrangian Relaxations: A Tractable Approach for Continuous Markov Random Fields

Dual decomposition approaches in nonconvex optimization may suffer from a duality gap. This poses a challenge when applying them directly to nonconvex problems such as MAP-inference in a Markov random field (MRF) with continuous state spaces. To eliminate such gaps, this paper considers a reformulation of the original nonconvex task in the space of measures. This infinite-dimensional reformulation is then approximated by a semi-infinite one, which is obtained via a piecewise polynomial discretization in the dual. We provide a geometric intuition behind the primal problem induced by the dual discretization and draw connections to optimization over moment spaces. In contrast to existing discretizations which suffer from a grid bias, we show that a piecewise polynomial discretization better preserves the continuous nature of our problem. Invoking results from optimal transport theory and convex algebraic geometry we reduce the semi-infinite program to a finite one and provide a practical implementation based on semidefinite programming. We show, experimentally and in theory, that the approach successfully reduces the duality gap. To showcase the scalability of our approach, we apply it to the stereo matching problem between two images.

Exploiting the Logits: Joint Sign Language Recognition and Spell-Correction

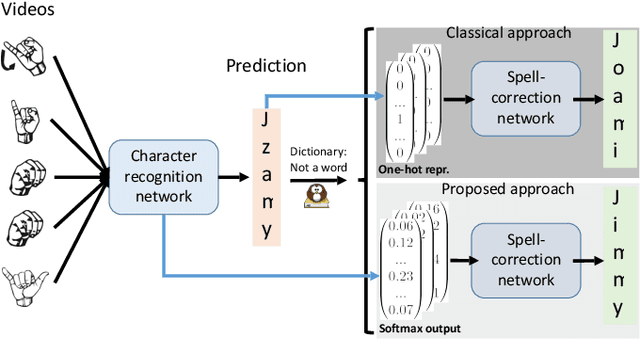
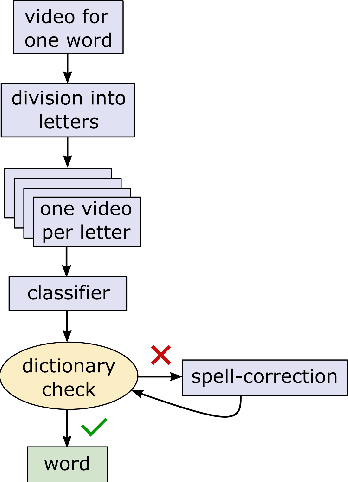
Machine learning techniques have excelled in the automatic semantic analysis of images, reaching human-level performances on challenging benchmarks. Yet, the semantic analysis of videos remains challenging due to the significantly higher dimensionality of the input data, respectively, the significantly higher need for annotated training examples. By studying the automatic recognition of German sign language videos, we demonstrate that on the relatively scarce training data of 2.800 videos, modern deep learning architectures for video analysis (such as ResNeXt) along with transfer learning on large gesture recognition tasks, can achieve about 75% character accuracy. Considering that this leaves us with a probability of under 25% that a 5 letter word is spelled correctly, spell-correction systems are crucial for producing readable outputs. The contribution of this paper is to propose a convolutional neural network for spell-correction that expects the softmax outputs of the character recognition network (instead of a misspelled word) as an input. We demonstrate that purely learning on softmax inputs in combination with scarce training data yields overfitting as the network learns the inputs by heart. In contrast, training the network on several variants of the logits of the classification output i.e. scaling by a constant factor, adding of random noise, mixing of softmax and hardmax inputs or purely training on hardmax inputs, leads to better generalization while benefitting from the significant information hidden in these outputs (that have 98% top-5 accuracy), yielding a readable text despite the comparably low character accuracy.

Fast Convex Relaxations using Graph Discretizations

Matching and partitioning problems are fundamentals of computer vision applications with examples in multilabel segmentation, stereo estimation and optical-flow computation. These tasks can be posed as non-convex energy minimization problems and solved near-globally optimal by recent convex lifting approaches. Yet, applying these techniques comes with a significant computational effort, reducing their feasibility in practical applications. We discuss spatial discretization of continuous partitioning problems into a graph structure, generalizing discretization onto a Cartesian grid. This setup allows us to faithfully work on super-pixel graphs constructed by SLIC or Cut-Pursuit, massively decreasing the computational effort for lifted partitioning problems compared to a Cartesian grid, while optimal energy values remain similar: The global matching is still solved near-globally optimally. We discuss this methodology in detail and show examples in multi-label segmentation by minimal partitions and stereo estimation, where we demonstrate that the proposed graph discretization technique can reduce the runtime as well as the memory consumption by up to a factor of 10 in comparison to classical pixelwise discretizations.

Inverting Gradients -- How easy is it to break privacy in federated learning?

The idea of federated learning is to collaboratively train a neural network on a server. Each user receives the current weights of the network and in turns sends parameter updates (gradients) based on local data. This protocol has been designed not only to train neural networks data-efficiently, but also to provide privacy benefits for users, as their input data remains on device and only parameter gradients are shared. In this paper we show that sharing parameter gradients is by no means secure: By exploiting a cosine similarity loss along with optimization methods from adversarial attacks, we are able to faithfully reconstruct images at high resolution from the knowledge of their parameter gradients, and demonstrate that such a break of privacy is possible even for trained deep networks. Moreover, we analyze the effects of architecture as well as parameters on the difficulty of reconstructing the input image, prove that any input to a fully connected layer can be reconstructed analytically independent of the remaining architecture, and show numerically that even averaging gradients over several iterations or several images does not protect the user's privacy in federated learning applications in computer vision.