The inexact power augmented Lagrangian method for constrained nonconvex optimization

This work introduces an unconventional inexact augmented Lagrangian method, where the augmenting term is a Euclidean norm raised to a power between one and two. The proposed algorithm is applicable to a broad class of constrained nonconvex minimization problems, that involve nonlinear equality constraints over a convex set under a mild regularity condition. First, we conduct a full complexity analysis of the method, leveraging an accelerated first-order algorithm for solving the H\"older-smooth subproblems. Next, we present an inexact proximal point method to tackle these subproblems, demonstrating that it achieves an improved convergence rate. Notably, this rate reduces to the best-known convergence rate for first-order methods when the augmenting term is a squared Euclidean norm. Our worst-case complexity results further show that using lower powers for the augmenting term leads to faster constraint satisfaction, albeit with a slower decrease in the dual residual. Numerical experiments support our theoretical findings, illustrating that this trade-off between constraint satisfaction and cost minimization is advantageous for certain practical problems.

Adaptive proximal gradient methods are universal without approximation

We show that adaptive proximal gradient methods for convex problems are not restricted to traditional Lipschitzian assumptions. Our analysis reveals that a class of linesearch-free methods is still convergent under mere local H\"older gradient continuity, covering in particular continuously differentiable semi-algebraic functions. To mitigate the lack of local Lipschitz continuity, popular approaches revolve around $\varepsilon$-oracles and/or linesearch procedures. In contrast, we exploit plain H\"older inequalities not entailing any approximation, all while retaining the linesearch-free nature of adaptive schemes. Furthermore, we prove full sequence convergence without prior knowledge of local H\"older constants nor of the order of H\"older continuity. In numerical experiments we present comparisons to baseline methods on diverse tasks from machine learning covering both the locally and the globally H\"older setting.

Lifting the Convex Conjugate in Lagrangian Relaxations: A Tractable Approach for Continuous Markov Random Fields

Dual decomposition approaches in nonconvex optimization may suffer from a duality gap. This poses a challenge when applying them directly to nonconvex problems such as MAP-inference in a Markov random field (MRF) with continuous state spaces. To eliminate such gaps, this paper considers a reformulation of the original nonconvex task in the space of measures. This infinite-dimensional reformulation is then approximated by a semi-infinite one, which is obtained via a piecewise polynomial discretization in the dual. We provide a geometric intuition behind the primal problem induced by the dual discretization and draw connections to optimization over moment spaces. In contrast to existing discretizations which suffer from a grid bias, we show that a piecewise polynomial discretization better preserves the continuous nature of our problem. Invoking results from optimal transport theory and convex algebraic geometry we reduce the semi-infinite program to a finite one and provide a practical implementation based on semidefinite programming. We show, experimentally and in theory, that the approach successfully reduces the duality gap. To showcase the scalability of our approach, we apply it to the stereo matching problem between two images.

Bregman Proximal Framework for Deep Linear Neural Networks

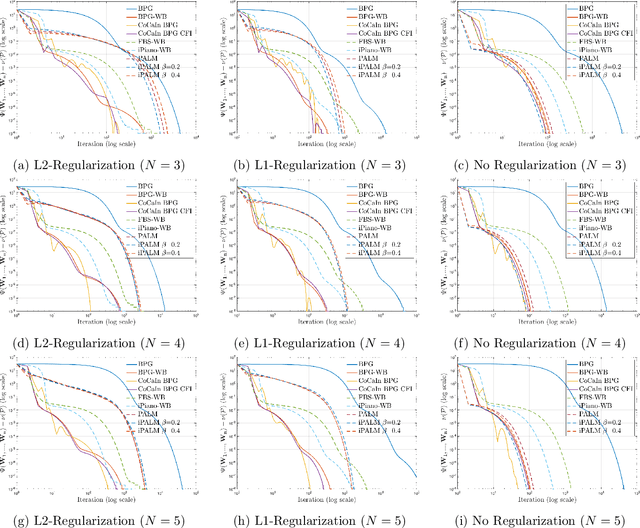
A typical assumption for the analysis of first order optimization methods is the Lipschitz continuity of the gradient of the objective function. However, for many practical applications this assumption is violated, including loss functions in deep learning. To overcome this issue, certain extensions based on generalized proximity measures known as Bregman distances were introduced. This initiated the development of the Bregman proximal gradient (BPG) algorithm and an inertial variant (momentum based) CoCaIn BPG, which however rely on problem dependent Bregman distances. In this paper, we develop Bregman distances for using BPG methods to train Deep Linear Neural Networks. The main implications of our results are strong convergence guarantees for these algorithms. We also propose several strategies for their efficient implementation, for example, closed form updates and a closed form expression for the inertial parameter of CoCaIn BPG. Moreover, the BPG method requires neither diminishing step sizes nor line search, unlike its corresponding Euclidean version. We numerically illustrate the competitiveness of the proposed methods compared to existing state of the art schemes.

Optimization of Inf-Convolution Regularized Nonconvex Composite Problems

In this work, we consider nonconvex composite problems that involve inf-convolution with a Legendre function, which gives rise to an anisotropic generalization of the proximal mapping and Moreau-envelope. In a convex setting such problems can be solved via alternating minimization of a splitting formulation, where the consensus constraint is penalized with a Legendre function. In contrast, for nonconvex models it is in general unclear that this approach yields stationary points to the infimal convolution problem. To this end we analytically investigate local regularity properties of the Moreau-envelope function under prox-regularity, which allows us to establish the equivalence between stationary points of the splitting model and the original inf-convolution model. We apply our theory to characterize stationary points of the penalty objective, which is minimized by the elastic averaging SGD (EASGD) method for distributed training. Numerically, we demonstrate the practical relevance of the proposed approach on the important task of distributed training of deep neural networks.

Discrete-Continuous ADMM for Transductive Inference in Higher-Order MRFs

This paper introduces a novel algorithm for transductive inference in higher-order MRFs, where the unary energies are parameterized by a variable classifier. The considered task is posed as a joint optimization problem in the continuous classifier parameters and the discrete label variables. In contrast to prior approaches such as convex relaxations, we propose an advantageous decoupling of the objective function into discrete and continuous subproblems and a novel, efficient optimization method related to ADMM. This approach preserves integrality of the discrete label variables and guarantees global convergence to a critical point. We demonstrate the advantages of our approach in several experiments including video object segmentation on the DAVIS data set and interactive image segmentation.

Sublabel-Accurate Convex Relaxation of Vectorial Multilabel Energies

Convex relaxations of nonconvex multilabel problems have been demonstrated to produce superior (provably optimal or near-optimal) solutions to a variety of classical computer vision problems. Yet, they are of limited practical use as they require a fine discretization of the label space, entailing a huge demand in memory and runtime. In this work, we propose the first sublabel accurate convex relaxation for vectorial multilabel problems. The key idea is that we approximate the dataterm of the vectorial labeling problem in a piecewise convex (rather than piecewise linear) manner. As a result we have a more faithful approximation of the original cost function that provides a meaningful interpretation for the fractional solutions of the relaxed convex problem. In numerous experiments on large-displacement optical flow estimation and on color image denoising we demonstrate that the computed solutions have superior quality while requiring much lower memory and runtime.

Sublabel-Accurate Relaxation of Nonconvex Energies

We propose a novel spatially continuous framework for convex relaxations based on functional lifting. Our method can be interpreted as a sublabel-accurate solution to multilabel problems. We show that previously proposed functional lifting methods optimize an energy which is linear between two labels and hence require (often infinitely) many labels for a faithful approximation. In contrast, the proposed formulation is based on a piecewise convex approximation and therefore needs far fewer labels. In comparison to recent MRF-based approaches, our method is formulated in a spatially continuous setting and shows less grid bias. Moreover, in a local sense, our formulation is the tightest possible convex relaxation. It is easy to implement and allows an efficient primal-dual optimization on GPUs. We show the effectiveness of our approach on several computer vision problems.