From concrete mixture to structural design -- a holistic optimization procedure in the presence of uncertainties

Designing civil structures such as bridges, dams or buildings is a complex task requiring many synergies from several experts. Each is responsible for different parts of the process. This is often done in a sequential manner, e.g. the structural engineer makes a design under the assumption of certain material properties (e.g. the strength class of the concrete), and then the material engineer optimizes the material with these restrictions. This paper proposes a holistic optimization procedure, which combines the concrete mixture design and structural simulations in a joint, forward workflow that we ultimately seek to invert. In this manner, new mixtures beyond standard ranges can be considered. Any design effort should account for the presence of uncertainties which can be aleatoric or epistemic as when data is used to calibrate physical models or identify models that fill missing links in the workflow. Inverting the causal relations established poses several challenges especially when these involve physics-based models which most often than not do not provide derivatives/sensitivities or when design constraints are present. To this end, we advocate Variational Optimization, with proposed extensions and appropriately chosen heuristics to overcome the aforementioned challenges. The proposed methodology is illustrated using the design of a precast concrete beam with the objective to minimize the global warming potential while satisfying a number of constraints associated with its load-bearing capacity after 28days according to the Eurocode, the demoulding time as computed by a complex nonlinear Finite Element model, and the maximum temperature during the hydration.

Multi-fidelity Constrained Optimization for Stochastic Black Box Simulators

Constrained optimization of the parameters of a simulator plays a crucial role in a design process. These problems become challenging when the simulator is stochastic, computationally expensive, and the parameter space is high-dimensional. One can efficiently perform optimization only by utilizing the gradient with respect to the parameters, but these gradients are unavailable in many legacy, black-box codes. We introduce the algorithm Scout-Nd (Stochastic Constrained Optimization for N dimensions) to tackle the issues mentioned earlier by efficiently estimating the gradient, reducing the noise of the gradient estimator, and applying multi-fidelity schemes to further reduce computational effort. We validate our approach on standard benchmarks, demonstrating its effectiveness in optimizing parameters highlighting better performance compared to existing methods.

A probabilistic, data-driven closure model for RANS simulations with aleatoric, model uncertainty

We propose a data-driven, closure model for Reynolds-averaged Navier-Stokes (RANS) simulations that incorporates aleatoric, model uncertainty. The proposed closure consists of two parts. A parametric one, which utilizes previously proposed, neural-network-based tensor basis functions dependent on the rate of strain and rotation tensor invariants. This is complemented by latent, random variables which account for aleatoric model errors. A fully Bayesian formulation is proposed, combined with a sparsity-inducing prior in order to identify regions in the problem domain where the parametric closure is insufficient and where stochastic corrections to the Reynolds stress tensor are needed. Training is performed using sparse, indirect data, such as mean velocities and pressures, in contrast to the majority of alternatives that require direct Reynolds stress data. For inference and learning, a Stochastic Variational Inference scheme is employed, which is based on Monte Carlo estimates of the pertinent objective in conjunction with the reparametrization trick. This necessitates derivatives of the output of the RANS solver, for which we developed an adjoint-based formulation. In this manner, the parametric sensitivities from the differentiable solver can be combined with the built-in, automatic differentiation capability of the neural network library in order to enable an end-to-end differentiable framework. We demonstrate the capability of the proposed model to produce accurate, probabilistic, predictive estimates for all flow quantities, even in regions where model errors are present, on a separated flow in the backward-facing step benchmark problem.

A reduced-order modeling framework for simulating signatures of faults in a bladed disk

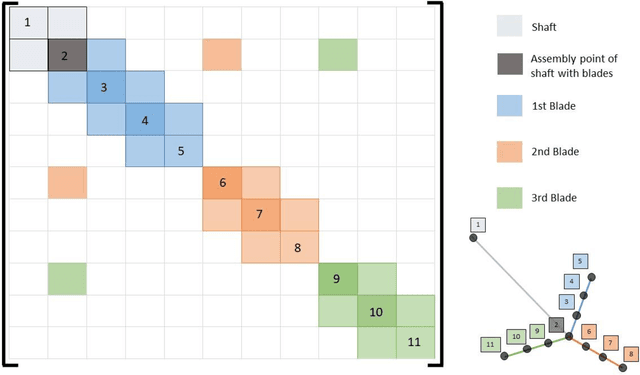
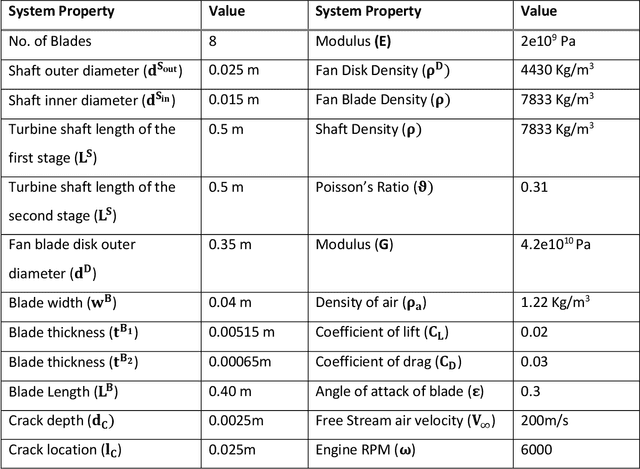
This paper reports a reduced-order modeling framework of bladed disks on a rotating shaft to simulate the vibration signature of faults like cracks in different components aiming towards simulated data-driven machine learning. We have employed lumped and one-dimensional analytical models of the subcomponents for better insight into the complex dynamic response. The framework seeks to address some of the challenges encountered in analyzing and optimizing fault detection and identification schemes for health monitoring of rotating turbomachinery, including aero-engines. We model the bladed disks and shafts by combining lumped elements and one-dimensional finite elements, leading to a coupled system. The simulation results are in good agreement with previously published data. We model the cracks in a blade analytically with their effective reduced stiffness approximation. Multiple types of faults are modeled, including cracks in the blades of single and two-stage bladed disks, Fan Blade Off (FBO), and Foreign Object Damage (FOD). We have applied aero-engine operational loading conditions to simulate realistic scenarios of online health monitoring. The proposed reduced-order simulation framework will have applications in probabilistic signal modeling, machine learning toward fault signature identification, and parameter estimation with measured vibration signals.

Physics-aware deep neural networks for surrogate modeling of turbulent natural convection

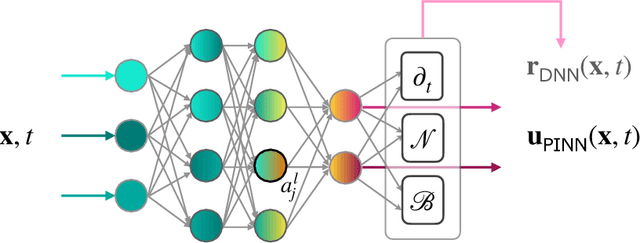
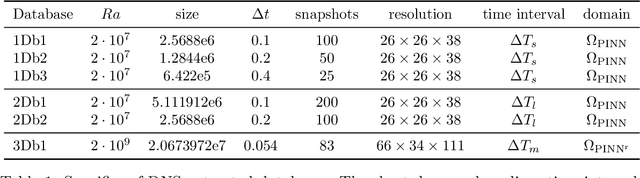
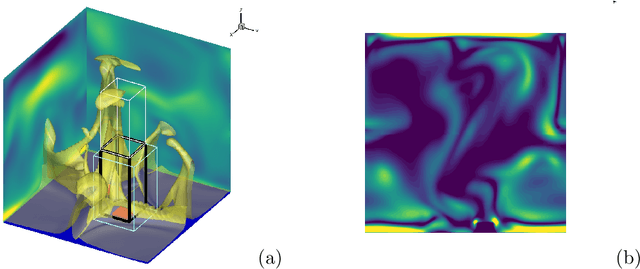
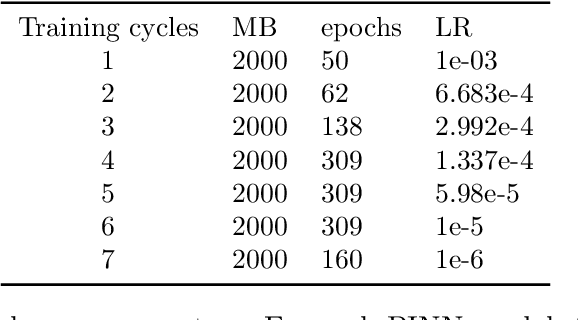
Recent works have explored the potential of machine learning as data-driven turbulence closures for RANS and LES techniques. Beyond these advances, the high expressivity and agility of physics-informed neural networks (PINNs) make them promising candidates for full fluid flow PDE modeling. An important question is whether this new paradigm, exempt from the traditional notion of discretization of the underlying operators very much connected to the flow scales resolution, is capable of sustaining high levels of turbulence characterized by multi-scale features? We investigate the use of PINNs surrogate modeling for turbulent Rayleigh-B{\'e}nard (RB) convection flows in rough and smooth rectangular cavities, mainly relying on DNS temperature data from the fluid bulk. We carefully quantify the computational requirements under which the formulation is capable of accurately recovering the flow hidden quantities. We then propose a new padding technique to distribute some of the scattered coordinates-at which PDE residuals are minimized-around the region of labeled data acquisition. We show how it comes to play as a regularization close to the training boundaries which are zones of poor accuracy for standard PINNs and results in a noticeable global accuracy improvement at iso-budget. Finally, we propose for the first time to relax the incompressibility condition in such a way that it drastically benefits the optimization search and results in a much improved convergence of the composite loss function. The RB results obtained at high Rayleigh number Ra = 2 $\bullet$ 10 9 are particularly impressive: the predictive accuracy of the surrogate over the entire half a billion DNS coordinates yields errors for all flow variables ranging between [0.3% -- 4%] in the relative L 2 norm, with a training relying only on 1.6% of the DNS data points.