Multi-fidelity Gaussian process surrogate modeling for regression problems in physics

One of the main challenges in surrogate modeling is the limited availability of data due to resource constraints associated with computationally expensive simulations. Multi-fidelity methods provide a solution by chaining models in a hierarchy with increasing fidelity, associated with lower error, but increasing cost. In this paper, we compare different multi-fidelity methods employed in constructing Gaussian process surrogates for regression. Non-linear autoregressive methods in the existing literature are primarily confined to two-fidelity models, and we extend these methods to handle more than two levels of fidelity. Additionally, we propose enhancements for an existing method incorporating delay terms by introducing a structured kernel. We demonstrate the performance of these methods across various academic and real-world scenarios. Our findings reveal that multi-fidelity methods generally have a smaller prediction error for the same computational cost as compared to the single-fidelity method, although their effectiveness varies across different scenarios.

Multi-fidelity Constrained Optimization for Stochastic Black Box Simulators

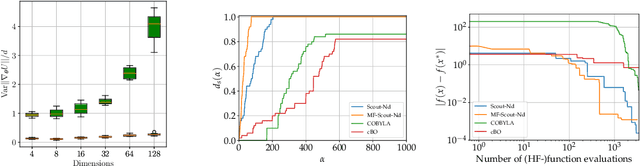
Constrained optimization of the parameters of a simulator plays a crucial role in a design process. These problems become challenging when the simulator is stochastic, computationally expensive, and the parameter space is high-dimensional. One can efficiently perform optimization only by utilizing the gradient with respect to the parameters, but these gradients are unavailable in many legacy, black-box codes. We introduce the algorithm Scout-Nd (Stochastic Constrained Optimization for N dimensions) to tackle the issues mentioned earlier by efficiently estimating the gradient, reducing the noise of the gradient estimator, and applying multi-fidelity schemes to further reduce computational effort. We validate our approach on standard benchmarks, demonstrating its effectiveness in optimizing parameters highlighting better performance compared to existing methods.