Multi-fidelity Gaussian process surrogate modeling for regression problems in physics

One of the main challenges in surrogate modeling is the limited availability of data due to resource constraints associated with computationally expensive simulations. Multi-fidelity methods provide a solution by chaining models in a hierarchy with increasing fidelity, associated with lower error, but increasing cost. In this paper, we compare different multi-fidelity methods employed in constructing Gaussian process surrogates for regression. Non-linear autoregressive methods in the existing literature are primarily confined to two-fidelity models, and we extend these methods to handle more than two levels of fidelity. Additionally, we propose enhancements for an existing method incorporating delay terms by introducing a structured kernel. We demonstrate the performance of these methods across various academic and real-world scenarios. Our findings reveal that multi-fidelity methods generally have a smaller prediction error for the same computational cost as compared to the single-fidelity method, although their effectiveness varies across different scenarios.

Context-aware learning of hierarchies of low-fidelity models for multi-fidelity uncertainty quantification

Multi-fidelity Monte Carlo methods leverage low-fidelity and surrogate models for variance reduction to make tractable uncertainty quantification even when numerically simulating the physical systems of interest with high-fidelity models is computationally expensive. This work proposes a context-aware multi-fidelity Monte Carlo method that optimally balances the costs of training low-fidelity models with the costs of Monte Carlo sampling. It generalizes the previously developed context-aware bi-fidelity Monte Carlo method to hierarchies of multiple models and to more general types of low-fidelity models. When training low-fidelity models, the proposed approach takes into account the context in which the learned low-fidelity models will be used, namely for variance reduction in Monte Carlo estimation, which allows it to find optimal trade-offs between training and sampling to minimize upper bounds of the mean-squared errors of the estimators for given computational budgets. This is in stark contrast to traditional surrogate modeling and model reduction techniques that construct low-fidelity models with the primary goal of approximating well the high-fidelity model outputs and typically ignore the context in which the learned models will be used in upstream tasks. The proposed context-aware multi-fidelity Monte Carlo method applies to hierarchies of a wide range of types of low-fidelity models such as sparse-grid and deep-network models. Numerical experiments with the gyrokinetic simulation code \textsc{Gene} show speedups of up to two orders of magnitude compared to standard estimators when quantifying uncertainties in small-scale fluctuations in confined plasma in fusion reactors. This corresponds to a runtime reduction from 72 days to about four hours on one node of the Lonestar6 supercomputer at the Texas Advanced Computing Center.

Neural Nets with a Newton Conjugate Gradient Method on Multiple GPUs

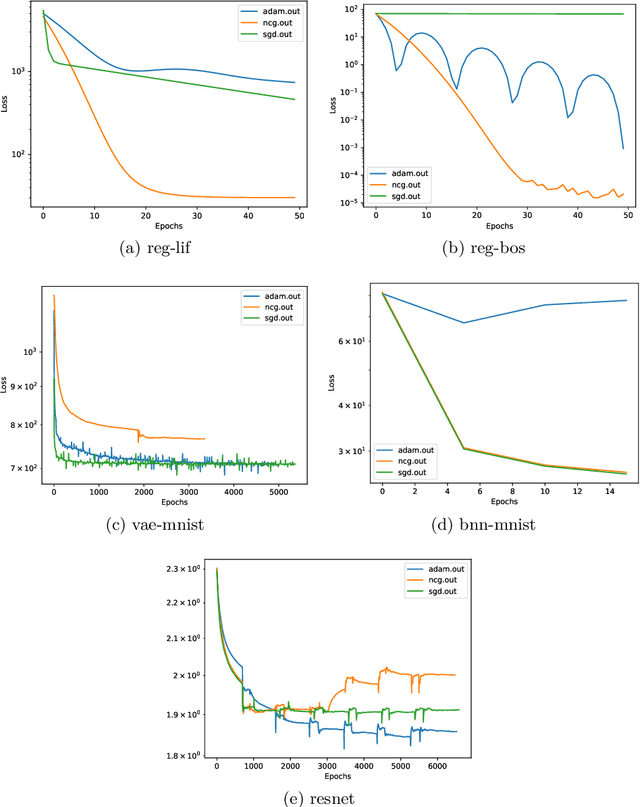
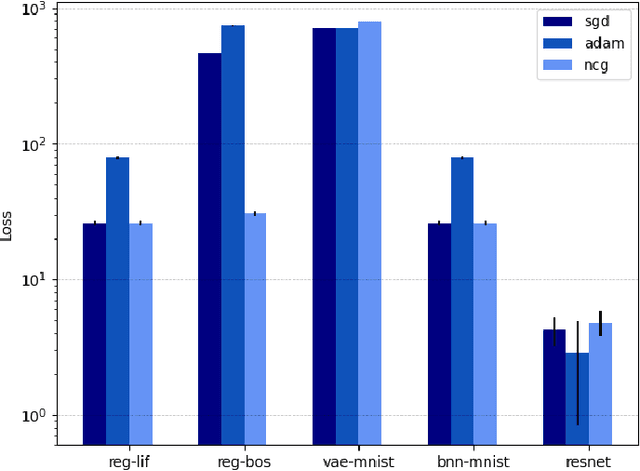
Training deep neural networks consumes increasing computational resource shares in many compute centers. Often, a brute force approach to obtain hyperparameter values is employed. Our goal is (1) to enhance this by enabling second-order optimization methods with fewer hyperparameters for large-scale neural networks and (2) to perform a survey of the performance optimizers for specific tasks to suggest users the best one for their problem. We introduce a novel second-order optimization method that requires the effect of the Hessian on a vector only and avoids the huge cost of explicitly setting up the Hessian for large-scale networks. We compare the proposed second-order method with two state-of-the-art optimizers on five representative neural network problems, including regression and very deep networks from computer vision or variational autoencoders. For the largest setup, we efficiently parallelized the optimizers with Horovod and applied it to a 8 GPU NVIDIA P100 (DGX-1) machine.