Sequential learning based PINNs to overcome temporal domain complexities in unsteady flow past flapping wings

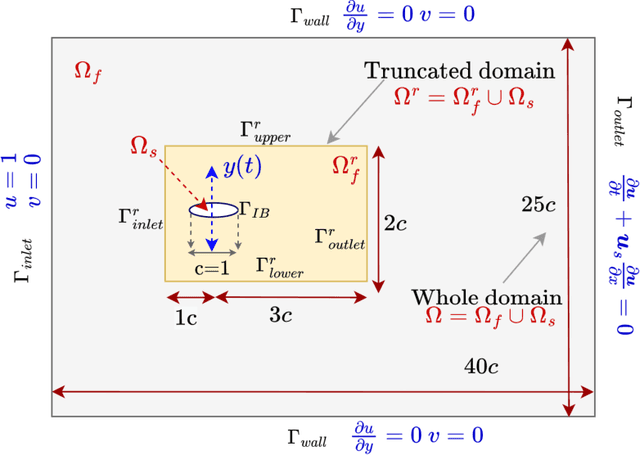
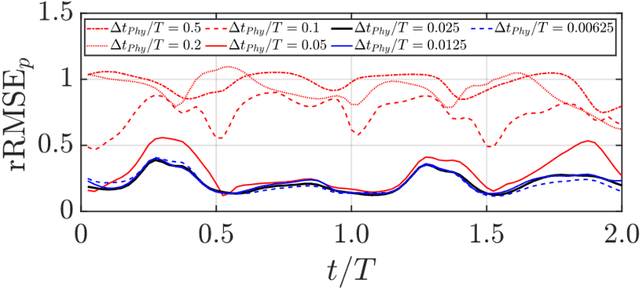
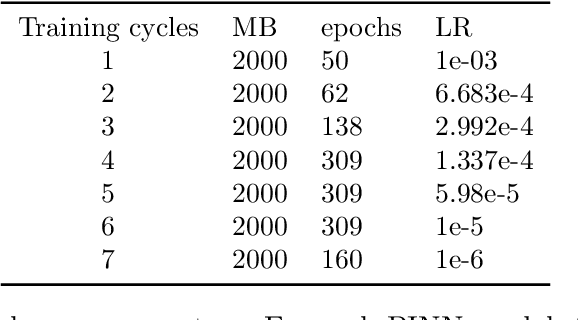
For a data-driven and physics combined modelling of unsteady flow systems with moving immersed boundaries, Sundar {\it et al.} introduced an immersed boundary-aware (IBA) framework, combining Physics-Informed Neural Networks (PINNs) and the immersed boundary method (IBM). This approach was beneficial because it avoided case-specific transformations to a body-attached reference frame. Building on this, we now address the challenges of long time integration in velocity reconstruction and pressure recovery by extending this IBA framework with sequential learning strategies. Key difficulties for PINNs in long time integration include temporal sparsity, long temporal domains and rich spectral content. To tackle these, a moving boundary-enabled PINN is developed, proposing two sequential learning strategies: - a time marching with gradual increase in time domain size, however, this approach struggles with error accumulation over long time domains; and - a time decomposition which divides the temporal domain into smaller segments, combined with transfer learning it effectively reduces error propagation and computational complexity. The key findings for modelling of incompressible unsteady flows past a flapping airfoil include: - for quasi-periodic flows, the time decomposition approach with preferential spatio-temporal sampling improves accuracy and efficiency for pressure recovery and aerodynamic load reconstruction, and, - for long time domains, decomposing it into smaller temporal segments and employing multiple sub-networks, simplifies the problem ensuring stability and reduced network sizes. This study highlights the limitations of traditional PINNs for long time integration of flow-structure interaction problems and demonstrates the benefits of decomposition-based strategies for addressing error accumulation, computational cost, and complex dynamics.

Understanding the training of PINNs for unsteady flow past a plunging foil through the lens of input subdomain level loss function gradients

Recently immersed boundary method-inspired physics-informed neural networks (PINNs) including the moving boundary-enabled PINNs (MB-PINNs) have shown the ability to accurately reconstruct velocity and recover pressure as a hidden variable for unsteady flow past moving bodies. Considering flow past a plunging foil, MB-PINNs were trained with global physics loss relaxation and also in conjunction with a physics-based undersampling method, obtaining good accuracy. The purpose of this study was to investigate which input spatial subdomain contributes to the training under the effect of physics loss relaxation and physics-based undersampling. In the context of MB-PINNs training, three spatial zones: the moving body, wake, and outer zones were defined. To quantify which spatial zone drives the training, two novel metrics are computed from the zonal loss component gradient statistics and the proportion of sample points in each zone. Results confirm that the learning indeed depends on the combined effect of the zonal loss component gradients and the proportion of points in each zone. Moreover, the dominant input zones are also the ones that have the strongest solution gradients in some sense.

Conformal Approach To Gaussian Process Surrogate Evaluation With Coverage Guarantees

Gaussian processes (GPs) are a Bayesian machine learning approach widely used to construct surrogate models for the uncertainty quantification of computer simulation codes in industrial applications. It provides both a mean predictor and an estimate of the posterior prediction variance, the latter being used to produce Bayesian credibility intervals. Interpreting these intervals relies on the Gaussianity of the simulation model as well as the well-specification of the priors which are not always appropriate. We propose to address this issue with the help of conformal prediction. In the present work, a method for building adaptive cross-conformal prediction intervals is proposed by weighting the non-conformity score with the posterior standard deviation of the GP. The resulting conformal prediction intervals exhibit a level of adaptivity akin to Bayesian credibility sets and display a significant correlation with the surrogate model local approximation error, while being free from the underlying model assumptions and having frequentist coverage guarantees. These estimators can thus be used for evaluating the quality of a GP surrogate model and can assist a decision-maker in the choice of the best prior for the specific application of the GP. The performance of the method is illustrated through a panel of numerical examples based on various reference databases. Moreover, the potential applicability of the method is demonstrated in the context of surrogate modeling of an expensive-to-evaluate simulator of the clogging phenomenon in steam generators of nuclear reactors.

Physics-informed neural networks modeling for systems with moving immersed boundaries: application to an unsteady flow past a plunging foil

Recently, physics informed neural networks (PINNs) have been explored extensively for solving various forward and inverse problems and facilitating querying applications in fluid mechanics applications. However, work on PINNs for unsteady flows past moving bodies, such as flapping wings is scarce. Earlier studies mostly relied on transferring to a body attached frame of reference which is restrictive towards handling multiple moving bodies or deforming structures. Hence, in the present work, an immersed boundary aware framework has been explored for developing surrogate models for unsteady flows past moving bodies. Specifically, simultaneous pressure recovery and velocity reconstruction from Immersed boundary method (IBM) simulation data has been investigated. While, efficacy of velocity reconstruction has been tested against the fine resolution IBM data, as a step further, the pressure recovered was compared with that of an arbitrary Lagrange Eulerian (ALE) based solver. Under this framework, two PINN variants, (i) a moving-boundary-enabled standard Navier-Stokes based PINN (MB-PINN), and, (ii) a moving-boundary-enabled IBM based PINN (MB-IBM-PINN) have been formulated. A fluid-solid partitioning of the physics losses in MB-IBM-PINN has been allowed, in order to investigate the effects of solid body points while training. This enables MB-IBM-PINN to match with the performance of MB-PINN under certain loss weighting conditions. MB-PINN is found to be superior to MB-IBM-PINN when {\it a priori} knowledge of the solid body position and velocity are available. To improve the data efficiency of MB-PINN, a physics based data sampling technique has also been investigated. It is observed that a suitable combination of physics constraint relaxation and physics based sampling can achieve a model performance comparable to the case of using all the data points, under a fixed training budget.

Machine learning with data assimilation and uncertainty quantification for dynamical systems: a review

Data Assimilation (DA) and Uncertainty quantification (UQ) are extensively used in analysing and reducing error propagation in high-dimensional spatial-temporal dynamics. Typical applications span from computational fluid dynamics (CFD) to geoscience and climate systems. Recently, much effort has been given in combining DA, UQ and machine learning (ML) techniques. These research efforts seek to address some critical challenges in high-dimensional dynamical systems, including but not limited to dynamical system identification, reduced order surrogate modelling, error covariance specification and model error correction. A large number of developed techniques and methodologies exhibit a broad applicability across numerous domains, resulting in the necessity for a comprehensive guide. This paper provides the first overview of the state-of-the-art researches in this interdisciplinary field, covering a wide range of applications. This review aims at ML scientists who attempt to apply DA and UQ techniques to improve the accuracy and the interpretability of their models, but also at DA and UQ experts who intend to integrate cutting-edge ML approaches to their systems. Therefore, this article has a special focus on how ML methods can overcome the existing limits of DA and UQ, and vice versa. Some exciting perspectives of this rapidly developing research field are also discussed.

Reduced-order modeling for parameterized large-eddy simulations of atmospheric pollutant dispersion

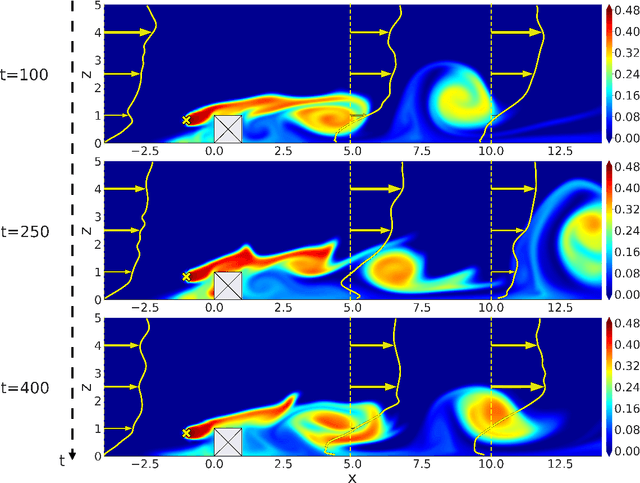
Mapping near-field pollutant concentration is essential to track accidental toxic plume dispersion in urban areas. By solving a large part of the turbulence spectrum, large-eddy simulations (LES) have the potential to accurately represent pollutant concentration spatial variability. Finding a way to synthesize this large amount of information to improve the accuracy of lower-fidelity operational models (e.g. providing better turbulence closure terms) is particularly appealing. This is a challenge in multi-query contexts, where LES become prohibitively costly to deploy to understand how plume flow and tracer dispersion change with various atmospheric and source parameters. To overcome this issue, we propose a non-intrusive reduced-order model combining proper orthogonal decomposition (POD) and Gaussian process regression (GPR) to predict LES field statistics of interest associated with tracer concentrations. GPR hyperpararameters are optimized component-by-component through a maximum a posteriori (MAP) procedure informed by POD. We provide a detailed analysis of the reducedorder model performance on a two-dimensional case study corresponding to a turbulent atmospheric boundary-layer flow over a surface-mounted obstacle. We show that near-source concentration heterogeneities upstream of the obstacle require a large number of POD modes to be well captured. We also show that the component-by-component optimization allows to capture the range of spatial scales in the POD modes, especially the shorter concentration patterns in the high-order modes. The reduced-order model predictions remain acceptable if the learning database is made of at least fifty to hundred LES snapshot providing a first estimation of the required budget to move towards more realistic atmospheric dispersion applications.

Physics-aware deep neural networks for surrogate modeling of turbulent natural convection

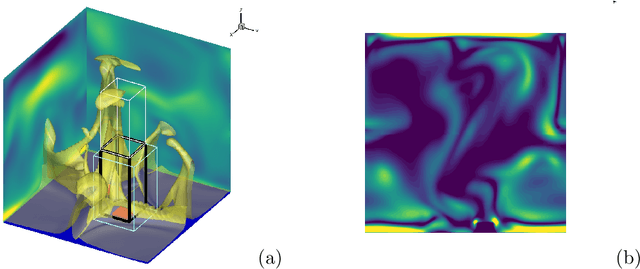
Recent works have explored the potential of machine learning as data-driven turbulence closures for RANS and LES techniques. Beyond these advances, the high expressivity and agility of physics-informed neural networks (PINNs) make them promising candidates for full fluid flow PDE modeling. An important question is whether this new paradigm, exempt from the traditional notion of discretization of the underlying operators very much connected to the flow scales resolution, is capable of sustaining high levels of turbulence characterized by multi-scale features? We investigate the use of PINNs surrogate modeling for turbulent Rayleigh-B{\'e}nard (RB) convection flows in rough and smooth rectangular cavities, mainly relying on DNS temperature data from the fluid bulk. We carefully quantify the computational requirements under which the formulation is capable of accurately recovering the flow hidden quantities. We then propose a new padding technique to distribute some of the scattered coordinates-at which PDE residuals are minimized-around the region of labeled data acquisition. We show how it comes to play as a regularization close to the training boundaries which are zones of poor accuracy for standard PINNs and results in a noticeable global accuracy improvement at iso-budget. Finally, we propose for the first time to relax the incompressibility condition in such a way that it drastically benefits the optimization search and results in a much improved convergence of the composite loss function. The RB results obtained at high Rayleigh number Ra = 2 $\bullet$ 10 9 are particularly impressive: the predictive accuracy of the surrogate over the entire half a billion DNS coordinates yields errors for all flow variables ranging between [0.3% -- 4%] in the relative L 2 norm, with a training relying only on 1.6% of the DNS data points.