Sequential learning based PINNs to overcome temporal domain complexities in unsteady flow past flapping wings

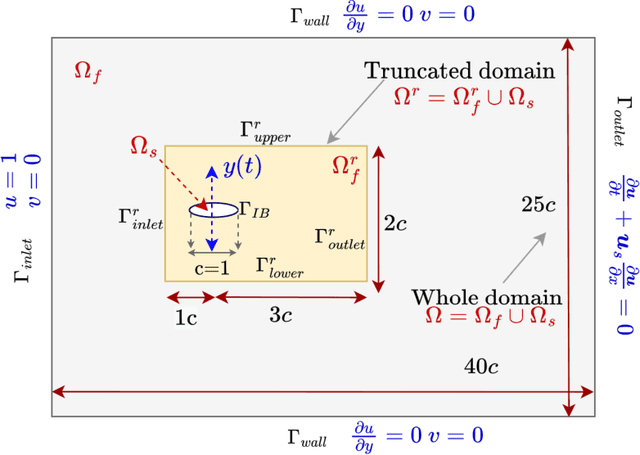
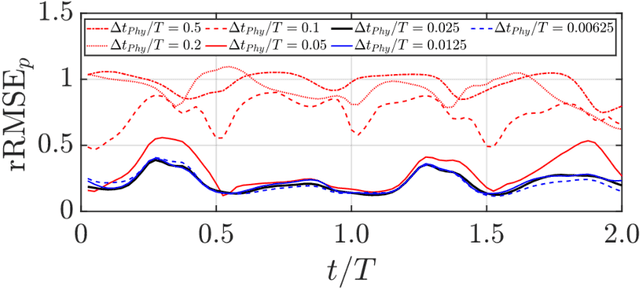
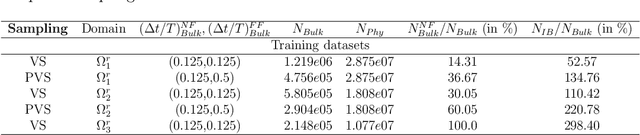
For a data-driven and physics combined modelling of unsteady flow systems with moving immersed boundaries, Sundar {\it et al.} introduced an immersed boundary-aware (IBA) framework, combining Physics-Informed Neural Networks (PINNs) and the immersed boundary method (IBM). This approach was beneficial because it avoided case-specific transformations to a body-attached reference frame. Building on this, we now address the challenges of long time integration in velocity reconstruction and pressure recovery by extending this IBA framework with sequential learning strategies. Key difficulties for PINNs in long time integration include temporal sparsity, long temporal domains and rich spectral content. To tackle these, a moving boundary-enabled PINN is developed, proposing two sequential learning strategies: - a time marching with gradual increase in time domain size, however, this approach struggles with error accumulation over long time domains; and - a time decomposition which divides the temporal domain into smaller segments, combined with transfer learning it effectively reduces error propagation and computational complexity. The key findings for modelling of incompressible unsteady flows past a flapping airfoil include: - for quasi-periodic flows, the time decomposition approach with preferential spatio-temporal sampling improves accuracy and efficiency for pressure recovery and aerodynamic load reconstruction, and, - for long time domains, decomposing it into smaller temporal segments and employing multiple sub-networks, simplifies the problem ensuring stability and reduced network sizes. This study highlights the limitations of traditional PINNs for long time integration of flow-structure interaction problems and demonstrates the benefits of decomposition-based strategies for addressing error accumulation, computational cost, and complex dynamics.

Understanding the training of PINNs for unsteady flow past a plunging foil through the lens of input subdomain level loss function gradients

Recently immersed boundary method-inspired physics-informed neural networks (PINNs) including the moving boundary-enabled PINNs (MB-PINNs) have shown the ability to accurately reconstruct velocity and recover pressure as a hidden variable for unsteady flow past moving bodies. Considering flow past a plunging foil, MB-PINNs were trained with global physics loss relaxation and also in conjunction with a physics-based undersampling method, obtaining good accuracy. The purpose of this study was to investigate which input spatial subdomain contributes to the training under the effect of physics loss relaxation and physics-based undersampling. In the context of MB-PINNs training, three spatial zones: the moving body, wake, and outer zones were defined. To quantify which spatial zone drives the training, two novel metrics are computed from the zonal loss component gradient statistics and the proportion of sample points in each zone. Results confirm that the learning indeed depends on the combined effect of the zonal loss component gradients and the proportion of points in each zone. Moreover, the dominant input zones are also the ones that have the strongest solution gradients in some sense.

Physics-informed neural networks modeling for systems with moving immersed boundaries: application to an unsteady flow past a plunging foil

Recently, physics informed neural networks (PINNs) have been explored extensively for solving various forward and inverse problems and facilitating querying applications in fluid mechanics applications. However, work on PINNs for unsteady flows past moving bodies, such as flapping wings is scarce. Earlier studies mostly relied on transferring to a body attached frame of reference which is restrictive towards handling multiple moving bodies or deforming structures. Hence, in the present work, an immersed boundary aware framework has been explored for developing surrogate models for unsteady flows past moving bodies. Specifically, simultaneous pressure recovery and velocity reconstruction from Immersed boundary method (IBM) simulation data has been investigated. While, efficacy of velocity reconstruction has been tested against the fine resolution IBM data, as a step further, the pressure recovered was compared with that of an arbitrary Lagrange Eulerian (ALE) based solver. Under this framework, two PINN variants, (i) a moving-boundary-enabled standard Navier-Stokes based PINN (MB-PINN), and, (ii) a moving-boundary-enabled IBM based PINN (MB-IBM-PINN) have been formulated. A fluid-solid partitioning of the physics losses in MB-IBM-PINN has been allowed, in order to investigate the effects of solid body points while training. This enables MB-IBM-PINN to match with the performance of MB-PINN under certain loss weighting conditions. MB-PINN is found to be superior to MB-IBM-PINN when {\it a priori} knowledge of the solid body position and velocity are available. To improve the data efficiency of MB-PINN, a physics based data sampling technique has also been investigated. It is observed that a suitable combination of physics constraint relaxation and physics based sampling can achieve a model performance comparable to the case of using all the data points, under a fixed training budget.