Simulation-informed deep learning for enhanced SWOT observations of fine-scale ocean dynamics

Oceanic processes at fine scales are crucial yet difficult to observe accurately due to limitations in satellite and in-situ measurements. The Surface Water and Ocean Topography (SWOT) mission provides high-resolution Sea Surface Height (SSH) data, though noise patterns often obscure fine scale structures. Current methods struggle with noisy data or require extensive supervised training, limiting their effectiveness on real-world observations. We introduce SIMPGEN (Simulation-Informed Metric and Prior for Generative Ensemble Networks), an unsupervised adversarial learning framework combining real SWOT observations with simulated reference data. SIMPGEN leverages wavelet-informed neural metrics to distinguish noisy from clean fields, guiding realistic SSH reconstructions. Applied to SWOT data, SIMPGEN effectively removes noise, preserving fine-scale features better than existing neural methods. This robust, unsupervised approach not only improves SWOT SSH data interpretation but also demonstrates strong potential for broader oceanographic applications, including data assimilation and super-resolution.

Observation-only learning of neural mapping schemes for gappy satellite-derived ocean colour parameters

Monitoring optical properties of coastal and open ocean waters is crucial to assessing the health of marine ecosystems. Deep learning offers a promising approach to address these ecosystem dynamics, especially in scenarios where gap-free ground-truth data is lacking, which poses a challenge for designing effective training frameworks. Using an advanced neural variational data assimilation scheme (called 4DVarNet), we introduce a comprehensive training framework designed to effectively train directly on gappy data sets. Using the Mediterranean Sea as a case study, our experiments not only highlight the high performance of the chosen neural network in reconstructing gap-free images from gappy datasets but also demonstrate its superior performance over state-of-the-art algorithms such as DInEOF and Direct Inversion, whether using CNN or UNet architectures.

Generalization performance of neural mapping schemes for the space-time interpolation of satellite-derived ocean colour datasets

Neural mapping schemes have become appealing approaches to deliver gap-free satellite-derived products for sea surface tracers. The generalization performance of these learning-based approaches naturally arises as a key challenge. This is particularly true for satellite-derived ocean colour products given the variety of bio-optical variables of interest, as well as the diversity of processes and scales involved. Considering region-specific and parameter-specific neural mapping schemes will result in substantial training costs. This study addresses generalization performance of neural mapping schemes to deliver gap-free satellite-derived ocean colour products. We develop a comprehensive experimental framework using real multi-sensor ocean colour datasets for two regions (the Mediterranean Sea and the North Sea) and a representative set of bio-optical parameters (Chlorophyll-a concentration, suspended particulate matter concentration, particulate backscattering coefficient). We consider several neural mapping schemes, and we report excellent generalization performance across regions and bio-optical parameters without any fine-tuning using appropriate dataset-specific normalization procedures. We discuss further how these results provide new insights towards the large-scale deployment of neural schemes for the processing of satellite-derived ocean colour datasets beyond case-study-specific demonstrations.

Neural Incremental Data Assimilation

Data assimilation is a central problem in many geophysical applications, such as weather forecasting. It aims to estimate the state of a potentially large system, such as the atmosphere, from sparse observations, supplemented by prior physical knowledge. The size of the systems involved and the complexity of the underlying physical equations make it a challenging task from a computational point of view. Neural networks represent a promising method of emulating the physics at low cost, and therefore have the potential to considerably improve and accelerate data assimilation. In this work, we introduce a deep learning approach where the physical system is modeled as a sequence of coarse-to-fine Gaussian prior distributions parametrized by a neural network. This allows us to define an assimilation operator, which is trained in an end-to-end fashion to minimize the reconstruction error on a dataset with different observation processes. We illustrate our approach on chaotic dynamical physical systems with sparse observations, and compare it to traditional variational data assimilation methods.

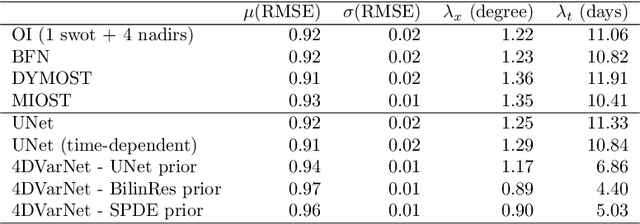
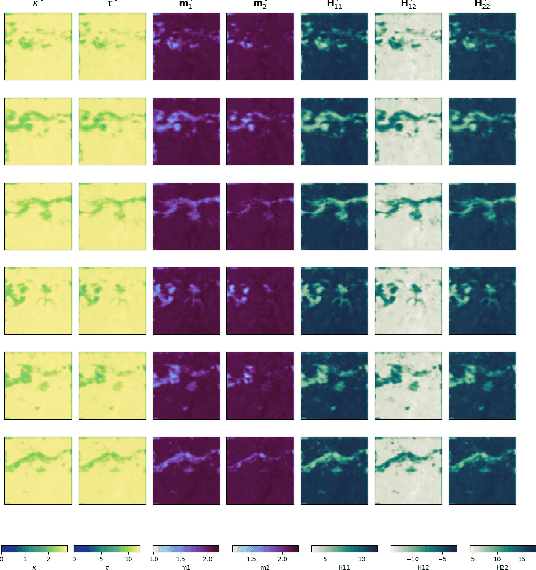
SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

Multi-Modal Learning-based Reconstruction of High-Resolution Spatial Wind Speed Fields

Wind speed at sea surface is a key quantity for a variety of scientific applications and human activities. Due to the non-linearity of the phenomenon, a complete description of such variable is made infeasible on both the small scale and large spatial extents. Methods relying on Data Assimilation techniques, despite being the state-of-the-art for Numerical Weather Prediction, can not provide the reconstructions with a spatial resolution that can compete with satellite imagery. In this work we propose a framework based on Variational Data Assimilation and Deep Learning concepts. This framework is applied to recover rich-in-time, high-resolution information on sea surface wind speed. We design our experiments using synthetic wind data and different sampling schemes for high-resolution and low-resolution versions of original data to emulate the real-world scenario of spatio-temporally heterogeneous observations. Extensive numerical experiments are performed to assess systematically the impact of low and high-resolution wind fields and in-situ observations on the model reconstruction performance. We show that in-situ observations with richer temporal resolution represent an added value in terms of the model reconstruction performance. We show how a multi-modal approach, that explicitly informs the model about the heterogeneity of the available observations, can improve the reconstruction task by exploiting the complementary information in spatial and local point-wise data. To conclude, we propose an analysis to test the robustness of the chosen framework against phase delay and amplitude biases in low-resolution data and against interruptions of in-situ observations supply at evaluation time

Online Calibration of Deep Learning Sub-Models for Hybrid Numerical Modeling Systems

Artificial intelligence and deep learning are currently reshaping numerical simulation frameworks by introducing new modeling capabilities. These frameworks are extensively investigated in the context of model correction and parameterization where they demonstrate great potential and often outperform traditional physical models. Most of these efforts in defining hybrid dynamical systems follow {offline} learning strategies in which the neural parameterization (called here sub-model) is trained to output an ideal correction. Yet, these hybrid models can face hard limitations when defining what should be a relevant sub-model response that would translate into a good forecasting performance. End-to-end learning schemes, also referred to as online learning, could address such a shortcoming by allowing the deep learning sub-models to train on historical data. However, defining end-to-end training schemes for the calibration of neural sub-models in hybrid systems requires working with an optimization problem that involves the solver of the physical equations. Online learning methodologies thus require the numerical model to be differentiable, which is not the case for most modeling systems. To overcome this difficulty and bypass the differentiability challenge of physical models, we present an efficient and practical online learning approach for hybrid systems. The method, called EGA for Euler Gradient Approximation, assumes an additive neural correction to the physical model, and an explicit Euler approximation of the gradients. We demonstrate that the EGA converges to the exact gradients in the limit of infinitely small time steps. Numerical experiments are performed on various case studies, including prototypical ocean-atmosphere dynamics. Results show significant improvements over offline learning, highlighting the potential of end-to-end online learning for hybrid modeling.

Neural SPDE solver for uncertainty quantification in high-dimensional space-time dynamics

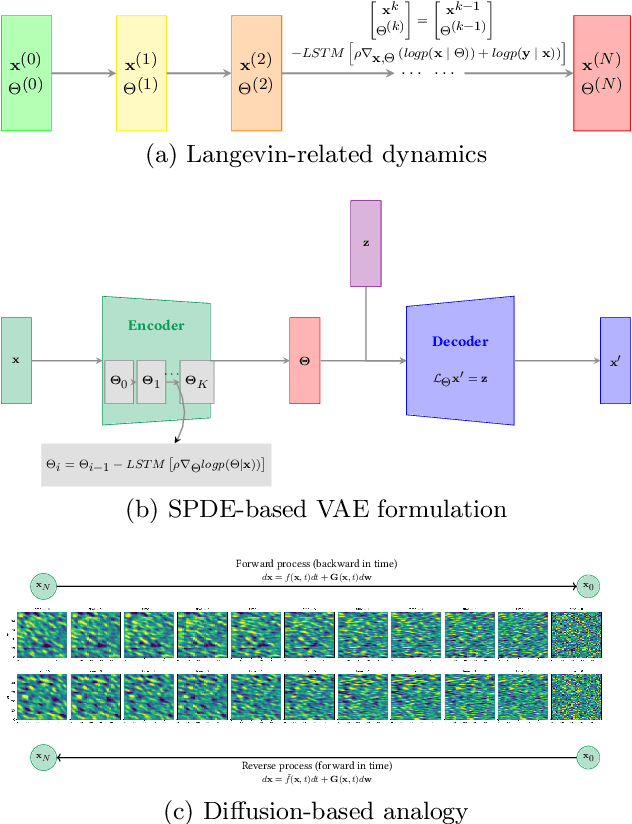
Historically, the interpolation of large geophysical datasets has been tackled using methods like Optimal Interpolation (OI) or model-based data assimilation schemes. However, the recent connection between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) introduced a novel approach to handle large datasets making use of sparse precision matrices in OI. Recent advancements in deep learning also addressed this issue by incorporating data assimilation into neural architectures: it treats the reconstruction task as a joint learning problem involving both prior model and solver as neural networks. Though, it requires further developments to quantify the associated uncertainties. In our work, we leverage SPDEbased Gaussian Processes to estimate complex prior models capable of handling nonstationary covariances in space and time. We develop a specific architecture able to learn both state and SPDE parameters as a neural SPDE solver, while providing the precisionbased analytical form of the SPDE sampling. The latter is used as a surrogate model along the data assimilation window. Because the prior is stochastic, we can easily draw samples from it and condition the members by our neural solver, allowing flexible estimation of the posterior distribution based on large ensemble. We demonstrate this framework on realistic Sea Surface Height datasets. Our solution improves the OI baseline, aligns with neural prior while enabling uncertainty quantification and online parameter estimation.

Gradient-free online learning of subgrid-scale dynamics with neural emulators

In this paper, we propose a generic algorithm to train machine learning-based subgrid parametrizations online, i.e., with $\textit{a posteriori}$ loss functions for non-differentiable numerical solvers. The proposed approach leverage neural emulators to train an approximation of the reduced state-space solver, which is then used to allows gradient propagation through temporal integration steps. The algorithm is able to recover most of the benefit of online strategies without having to compute the gradient of the original solver. It is demonstrated that training the neural emulator and parametrization components separately with respective loss quantities is necessary in order to minimize the propagation of some approximation bias.

Building a Safer Maritime Environment Through Multi-Path Long-Term Vessel Trajectory Forecasting

Maritime transport is paramount to global economic growth and environmental sustainability. In this regard, the Automatic Identification System (AIS) data plays a significant role by offering real-time streaming data on vessel movement, which allows for enhanced traffic surveillance, assisting in vessel safety by avoiding vessel-to-vessel collisions and proactively preventing vessel-to-whale ones. This paper tackles an intrinsic problem to trajectory forecasting: the effective multi-path long-term vessel trajectory forecasting on engineered sequences of AIS data. We utilize an encoder-decoder model with Bidirectional Long Short-Term Memory Networks (Bi-LSTM) to predict the next 12 hours of vessel trajectories using 1 to 3 hours of AIS data. We feed the model with probabilistic features engineered from the AIS data that refer to the potential route and destination of each trajectory so that the model, leveraging convolutional layers for spatial feature learning and a position-aware attention mechanism that increases the importance of recent timesteps of a sequence during temporal feature learning, forecasts the vessel trajectory taking the potential route and destination into account. The F1 Score of these features is approximately 85% and 75%, indicating their efficiency in supplementing the neural network. We trialed our model in the Gulf of St. Lawrence, one of the North Atlantic Right Whales (NARW) habitats, achieving an R2 score exceeding 98% with varying techniques and features. Despite the high R2 score being attributed to well-defined shipping lanes, our model demonstrates superior complex decision-making during path selection. In addition, our model shows enhanced accuracy, with average and median forecasting errors of 11km and 6km, respectively. Our study confirms the potential of geographical data engineering and trajectory forecasting models for preserving marine life species.