SPDE priors for uncertainty quantification of end-to-end neural data assimilation schemes

The spatio-temporal interpolation of large geophysical datasets has historically been adressed by Optimal Interpolation (OI) and more sophisticated model-based or data-driven DA techniques. In the last ten years, the link established between Stochastic Partial Differential Equations (SPDE) and Gaussian Markov Random Fields (GMRF) opened a new way of handling both large datasets and physically-induced covariance matrix in Optimal Interpolation. Recent advances in the deep learning community also enables to adress this problem as neural architecture embedding data assimilation variational framework. The reconstruction task is seen as a joint learning problem of the prior involved in the variational inner cost and the gradient-based minimization of the latter: both prior models and solvers are stated as neural networks with automatic differentiation which can be trained by minimizing a loss function, typically stated as the mean squared error between some ground truth and the reconstruction. In this work, we draw from the SPDE-based Gaussian Processes to estimate complex prior models able to handle non-stationary covariances in both space and time and provide a stochastic framework for interpretability and uncertainty quantification. Our neural variational scheme is modified to embed an augmented state formulation with both state and SPDE parametrization to estimate. Instead of a neural prior, we use a stochastic PDE as surrogate model along the data assimilation window. The training involves a loss function for both reconstruction task and SPDE prior model, where the likelihood of the SPDE parameters given the true states is involved in the training. Because the prior is stochastic, we can easily draw samples in the prior distribution before conditioning to provide a flexible way to estimate the posterior distribution based on thousands of members.

Turning Normalizing Flows into Monge Maps with Geodesic Gaussian Preserving Flows

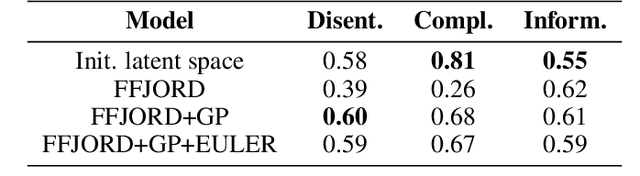
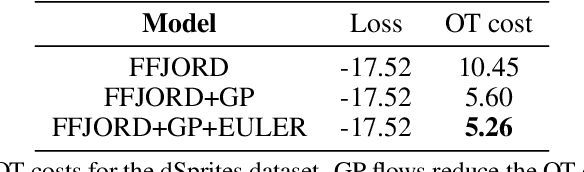
Normalizing Flows (NF) are powerful likelihood-based generative models that are able to trade off between expressivity and tractability to model complex densities. A now well established research avenue leverages optimal transport (OT) and looks for Monge maps, i.e. models with minimal effort between the source and target distributions. This paper introduces a method based on Brenier's polar factorization theorem to transform any trained NF into a more OT-efficient version without changing the final density. We do so by learning a rearrangement of the source (Gaussian) distribution that minimizes the OT cost between the source and the final density. We further constrain the path leading to the estimated Monge map to lie on a geodesic in the space of volume-preserving diffeomorphisms thanks to Euler's equations. The proposed method leads to smooth flows with reduced OT cost for several existing models without affecting the model performance.