Busemann Functions in the Wasserstein Space: Existence, Closed-Forms, and Applications to Slicing

The Busemann function has recently found much interest in a variety of geometric machine learning problems, as it naturally defines projections onto geodesic rays of Riemannian manifolds and generalizes the notion of hyperplanes. As several sources of data can be conveniently modeled as probability distributions, it is natural to study this function in the Wasserstein space, which carries a rich formal Riemannian structure induced by Optimal Transport metrics. In this work, we investigate the existence and computation of Busemann functions in Wasserstein space, which admits geodesic rays. We establish closed-form expressions in two important cases: one-dimensional distributions and Gaussian measures. These results enable explicit projection schemes for probability distributions on $\mathbb{R}$, which in turn allow us to define novel Sliced-Wasserstein distances over Gaussian mixtures and labeled datasets. We demonstrate the efficiency of those original schemes on synthetic datasets as well as transfer learning problems.

Bridging Arbitrary and Tree Metrics via Differentiable Gromov Hyperbolicity

Trees and the associated shortest-path tree metrics provide a powerful framework for representing hierarchical and combinatorial structures in data. Given an arbitrary metric space, its deviation from a tree metric can be quantified by Gromov's $\delta$-hyperbolicity. Nonetheless, designing algorithms that bridge an arbitrary metric to its closest tree metric is still a vivid subject of interest, as most common approaches are either heuristical and lack guarantees, or perform moderately well. In this work, we introduce a novel differentiable optimization framework, coined DeltaZero, that solves this problem. Our method leverages a smooth surrogate for Gromov's $\delta$-hyperbolicity which enables a gradient-based optimization, with a tractable complexity. The corresponding optimization procedure is derived from a problem with better worst case guarantees than existing bounds, and is justified statistically. Experiments on synthetic and real-world datasets demonstrate that our method consistently achieves state-of-the-art distortion.

Train Till You Drop: Towards Stable and Robust Source-free Unsupervised 3D Domain Adaptation

We tackle the challenging problem of source-free unsupervised domain adaptation (SFUDA) for 3D semantic segmentation. It amounts to performing domain adaptation on an unlabeled target domain without any access to source data; the available information is a model trained to achieve good performance on the source domain. A common issue with existing SFUDA approaches is that performance degrades after some training time, which is a by product of an under-constrained and ill-posed problem. We discuss two strategies to alleviate this issue. First, we propose a sensible way to regularize the learning problem. Second, we introduce a novel criterion based on agreement with a reference model. It is used (1) to stop the training when appropriate and (2) as validator to select hyperparameters without any knowledge on the target domain. Our contributions are easy to implement and readily amenable for all SFUDA methods, ensuring stable improvements over all baselines. We validate our findings on various 3D lidar settings, achieving state-of-the-art performance. The project repository (with code) is: github.com/valeoai/TTYD.

Sliced-Wasserstein Distances and Flows on Cartan-Hadamard Manifolds

While many Machine Learning methods were developed or transposed on Riemannian manifolds to tackle data with known non Euclidean geometry, Optimal Transport (OT) methods on such spaces have not received much attention. The main OT tool on these spaces is the Wasserstein distance which suffers from a heavy computational burden. On Euclidean spaces, a popular alternative is the Sliced-Wasserstein distance, which leverages a closed-form solution of the Wasserstein distance in one dimension, but which is not readily available on manifolds. In this work, we derive general constructions of Sliced-Wasserstein distances on Cartan-Hadamard manifolds, Riemannian manifolds with non-positive curvature, which include among others Hyperbolic spaces or the space of Symmetric Positive Definite matrices. Then, we propose different applications. Additionally, we derive non-parametric schemes to minimize these new distances by approximating their Wasserstein gradient flows.

Distributional Reduction: Unifying Dimensionality Reduction and Clustering with Gromov-Wasserstein Projection

Unsupervised learning aims to capture the underlying structure of potentially large and high-dimensional datasets. Traditionally, this involves using dimensionality reduction methods to project data onto interpretable spaces or organizing points into meaningful clusters. In practice, these methods are used sequentially, without guaranteeing that the clustering aligns well with the conducted dimensionality reduction. In this work, we offer a fresh perspective: that of distributions. Leveraging tools from optimal transport, particularly the Gromov-Wasserstein distance, we unify clustering and dimensionality reduction into a single framework called distributional reduction. This allows us to jointly address clustering and dimensionality reduction with a single optimization problem. Through comprehensive experiments, we highlight the versatility and interpretability of our method and show that it outperforms existing approaches across a variety of image and genomics datasets.

Interpolating between Clustering and Dimensionality Reduction with Gromov-Wasserstein

We present a versatile adaptation of existing dimensionality reduction (DR) objectives, enabling the simultaneous reduction of both sample and feature sizes. Correspondances between input and embedding samples are computed through a semi-relaxed Gromov-Wasserstein optimal transport (OT) problem. When the embedding sample size matches that of the input, our model recovers classical popular DR models. When the embedding's dimensionality is unconstrained, we show that the OT plan delivers a competitive hard clustering. We emphasize the importance of intermediate stages that blend DR and clustering for summarizing real data and apply our method to visualize datasets of images.

Optimal Transport with Adaptive Regularisation

Regularising the primal formulation of optimal transport (OT) with a strictly convex term leads to enhanced numerical complexity and a denser transport plan. Many formulations impose a global constraint on the transport plan, for instance by relying on entropic regularisation. As it is more expensive to diffuse mass for outlier points compared to central ones, this typically results in a significant imbalance in the way mass is spread across the points. This can be detrimental for some applications where a minimum of smoothing is required per point. To remedy this, we introduce OT with Adaptive RegularIsation (OTARI), a new formulation of OT that imposes constraints on the mass going in or/and out of each point. We then showcase the benefits of this approach for domain adaptation.

Match-And-Deform: Time Series Domain Adaptation through Optimal Transport and Temporal Alignment

While large volumes of unlabeled data are usually available, associated labels are often scarce. The unsupervised domain adaptation problem aims at exploiting labels from a source domain to classify data from a related, yet different, target domain. When time series are at stake, new difficulties arise as temporal shifts may appear in addition to the standard feature distribution shift. In this paper, we introduce the Match-And-Deform (MAD) approach that aims at finding correspondences between the source and target time series while allowing temporal distortions. The associated optimization problem simultaneously aligns the series thanks to an optimal transport loss and the time stamps through dynamic time warping. When embedded into a deep neural network, MAD helps learning new representations of time series that both align the domains and maximize the discriminative power of the network. Empirical studies on benchmark datasets and remote sensing data demonstrate that MAD makes meaningful sample-to-sample pairing and time shift estimation, reaching similar or better classification performance than state-of-the-art deep time series domain adaptation strategies.

Fast Optimal Transport through Sliced Wasserstein Generalized Geodesics

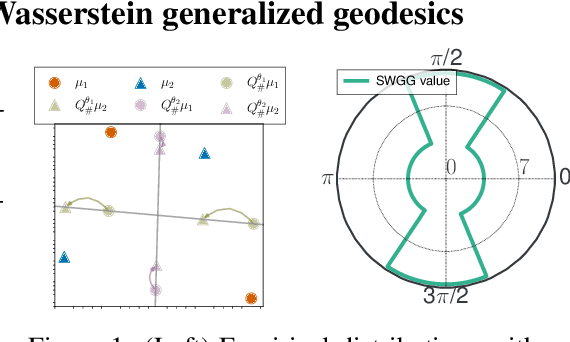
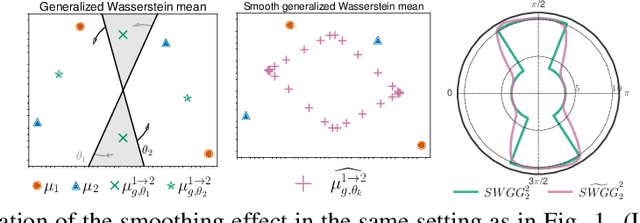
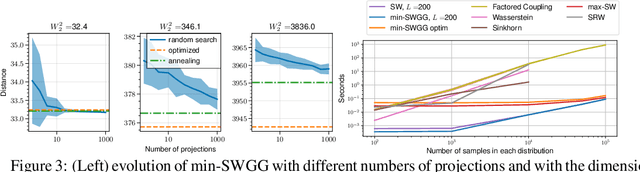
Wasserstein distance (WD) and the associated optimal transport plan have been proven useful in many applications where probability measures are at stake. In this paper, we propose a new proxy of the squared WD, coined min-SWGG, that is based on the transport map induced by an optimal one-dimensional projection of the two input distributions. We draw connections between min-SWGG and Wasserstein generalized geodesics in which the pivot measure is supported on a line. We notably provide a new closed form for the exact Wasserstein distance in the particular case of one of the distributions supported on a line allowing us to derive a fast computational scheme that is amenable to gradient descent optimization. We show that min-SWGG is an upper bound of WD and that it has a complexity similar to as Sliced-Wasserstein, with the additional feature of providing an associated transport plan. We also investigate some theoretical properties such as metricity, weak convergence, computational and topological properties. Empirical evidences support the benefits of min-SWGG in various contexts, from gradient flows, shape matching and image colorization, among others.

Joint multi-modal Self-Supervised pre-training in Remote Sensing: Application to Methane Source Classification

With the current ubiquity of deep learning methods to solve computer vision and remote sensing specific tasks, the need for labelled data is growing constantly. However, in many cases, the annotation process can be long and tedious depending on the expertise needed to perform reliable annotations. In order to alleviate this need for annotations, several self-supervised methods have recently been proposed in the literature. The core principle behind these methods is to learn an image encoder using solely unlabelled data samples. In earth observation, there are opportunities to exploit domain-specific remote sensing image data in order to improve these methods. Specifically, by leveraging the geographical position associated with each image, it is possible to cross reference a location captured from multiple sensors, leading to multiple views of the same locations. In this paper, we briefly review the core principles behind so-called joint-embeddings methods and investigate the usage of multiple remote sensing modalities in self-supervised pre-training. We evaluate the final performance of the resulting encoders on the task of methane source classification.