Match-And-Deform: Time Series Domain Adaptation through Optimal Transport and Temporal Alignment

While large volumes of unlabeled data are usually available, associated labels are often scarce. The unsupervised domain adaptation problem aims at exploiting labels from a source domain to classify data from a related, yet different, target domain. When time series are at stake, new difficulties arise as temporal shifts may appear in addition to the standard feature distribution shift. In this paper, we introduce the Match-And-Deform (MAD) approach that aims at finding correspondences between the source and target time series while allowing temporal distortions. The associated optimization problem simultaneously aligns the series thanks to an optimal transport loss and the time stamps through dynamic time warping. When embedded into a deep neural network, MAD helps learning new representations of time series that both align the domains and maximize the discriminative power of the network. Empirical studies on benchmark datasets and remote sensing data demonstrate that MAD makes meaningful sample-to-sample pairing and time shift estimation, reaching similar or better classification performance than state-of-the-art deep time series domain adaptation strategies.

Time Series Alignment with Global Invariances

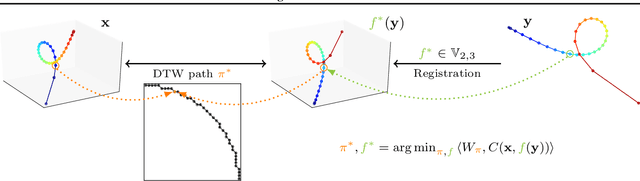
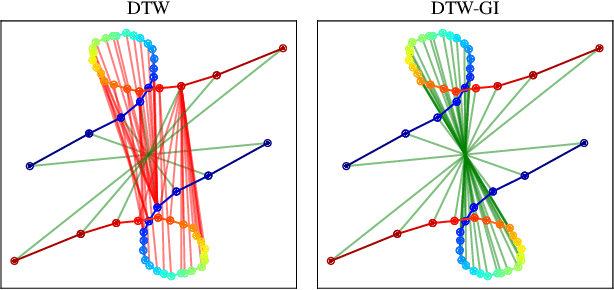
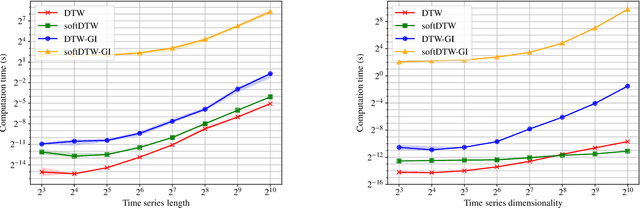
In this work we address the problem of comparing time series while taking into account both feature space transformation and temporal variability. The proposed framework combines a latent global transformation of the feature space with the widely used Dynamic Time Warping (DTW). The latent global transformation captures the feature invariance while the DTW (or its smooth counterpart soft-DTW) deals with the temporal shifts. We cast the problem as a joint optimization over the global transformation and the temporal alignments. The versatility of our framework allows for several variants depending on the invariance class at stake. Among our contributions we define a differentiable loss for time series and present two algorithms for the computation of time series barycenters under our new geometry. We illustrate the interest of our approach on both simulated and real world data.

Early Classification for Agricultural Monitoring from Satellite Time Series

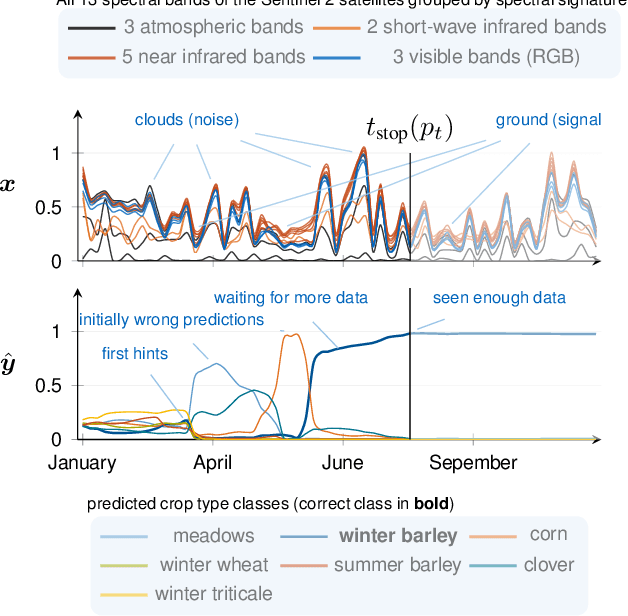
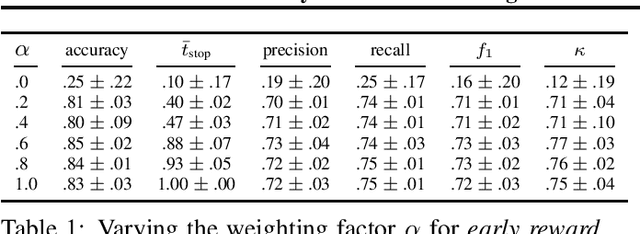
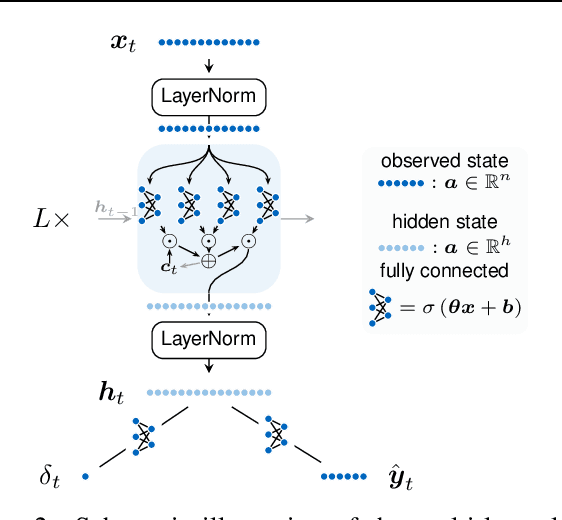
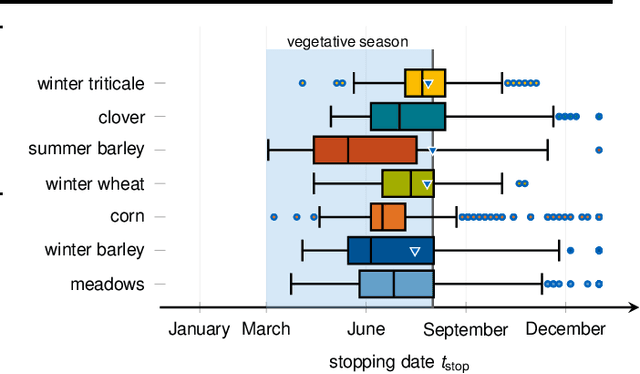
In this work, we introduce a recently developed early classification mechanism to satellite-based agricultural monitoring. It augments existing classification models by an additional stopping probability based on the previously seen information. This mechanism is end-to-end trainable and derives its stopping decision solely from the observed satellite data. We show results on field parcels in central Europe where sufficient ground truth data is available for an empiric evaluation of the results with local phenological information obtained from authorities. We observe that the recurrent neural network outfitted with this early classification mechanism was able to distinguish the many of the crop types before the end of the vegetative period. Further, we associated these stopping times with evaluated ground truth information and saw that the times of classification were related to characteristic events of the observed plants' phenology.

Learning Interpretable Shapelets for Time Series Classification through Adversarial Regularization

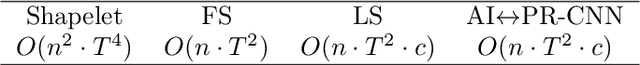
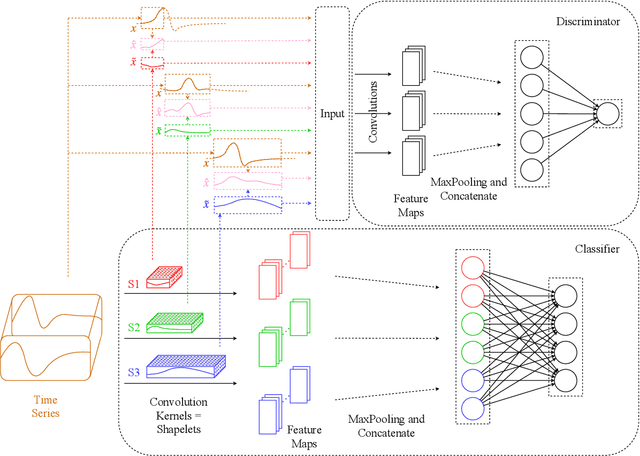
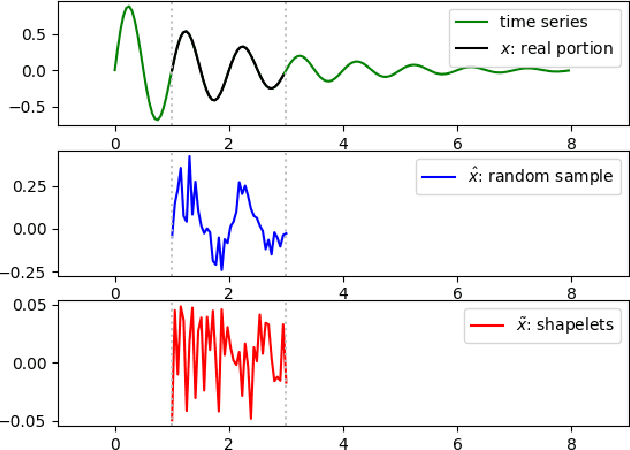
Times series classification can be successfully tackled by jointly learning a shapelet-based representation of the series in the dataset and classifying the series according to this representation. However, although the learned shapelets are discriminative, they are not always similar to pieces of a real series in the dataset. This makes it difficult to interpret the decision, i.e. difficult to analyze if there are particular behaviors in a series that triggered the decision. In this paper, we make use of a simple convolutional network to tackle the time series classification task and we introduce an adversarial regularization to constrain the model to learn more interpretable shapelets. Our classification results on all the usual time series benchmarks are comparable with the results obtained by similar state-of-the-art algorithms but our adversarially regularized method learns shapelets that are, by design, interpretable.

Sliced Gromov-Wasserstein

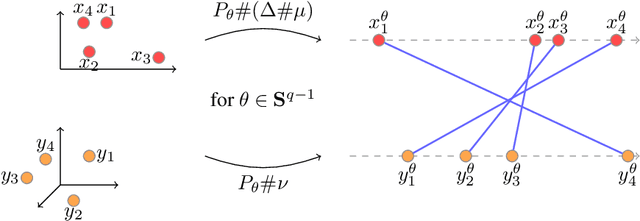
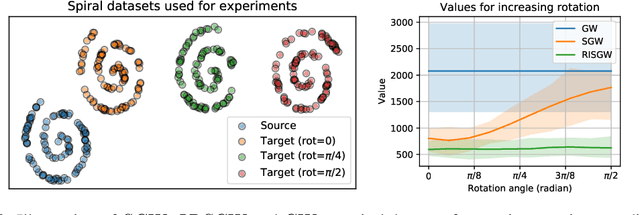
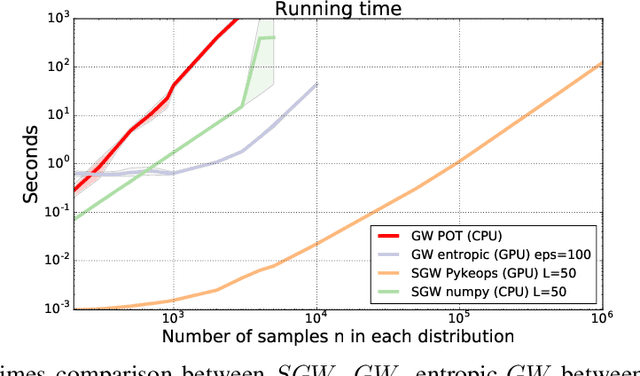
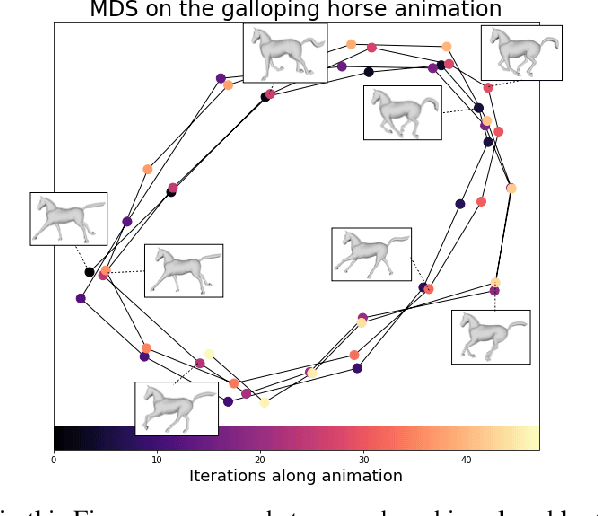
Recently used in various machine learning contexts, the Gromov-Wasserstein distance (GW) allows for comparing distributions that do not necessarily lie in the same metric space. However, this Optimal Transport (OT) distance requires solving a complex non convex quadratic program which is most of the time very costly both in time and memory. Contrary to GW, the Wasserstein distance (W) enjoys several properties (e.g. duality) that permit large scale optimization. Among those, the Sliced Wasserstein (SW) distance exploits the direct solution of W on the line, that only requires sorting discrete samples in 1D. This paper propose a new divergence based on GW akin to SW. We first derive a closed form for GW when dealing with 1D distributions, based on a new result for the related quadratic assignment problem. We then define a novel OT discrepancy that can deal with large scale distributions via a slicing approach and we show how it relates to the GW distance while being $O(n^2)$ to compute. We illustrate the behavior of this so called Sliced Gromov-Wasserstein (SGW) discrepancy in experiments where we demonstrate its ability to tackle similar problems as GW while being several order of magnitudes faster to compute

End-to-end Learning for Early Classification of Time Series

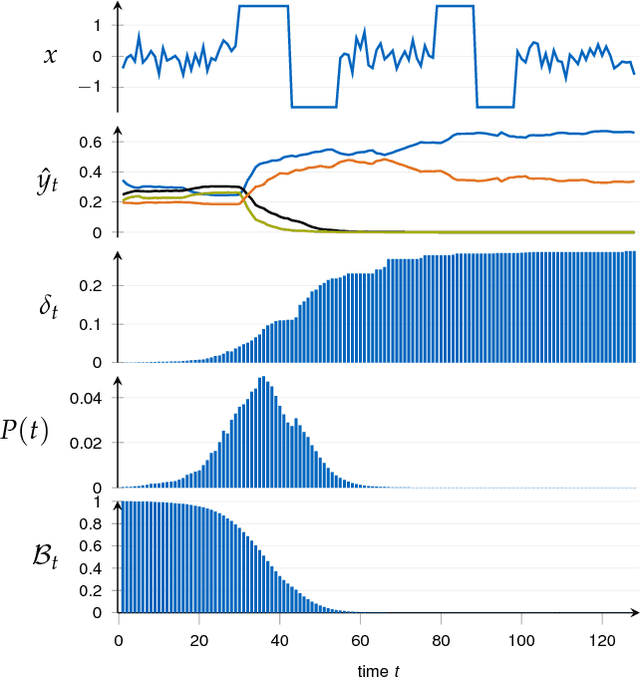
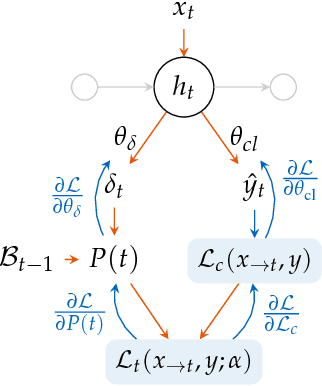
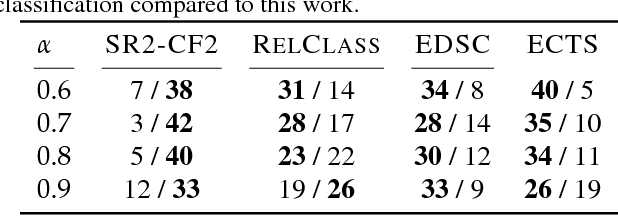
Classification of time series is a topical issue in machine learning. While accuracy stands for the most important evaluation criterion, some applications require decisions to be made as early as possible. Optimization should then target a compromise between earliness, i.e., a capacity of providing a decision early in the sequence, and accuracy. In this work, we propose a generic, end-to-end trainable framework for early classification of time series. This framework embeds a learnable decision mechanism that can be plugged into a wide range of already existing models. We present results obtained with deep neural networks on a diverse set of time series classification problems. Our approach compares well to state-of-the-art competitors while being easily adaptable by any existing neural network topology that evaluates a hidden state at each time step.

Fused Gromov-Wasserstein distance for structured objects: theoretical foundations and mathematical properties

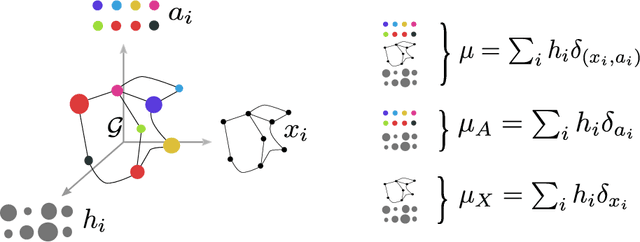
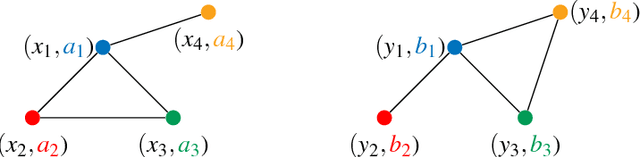
Optimal transport theory has recently found many applications in machine learning thanks to its capacity for comparing various machine learning objects considered as distributions. The Kantorovitch formulation, leading to the Wasserstein distance, focuses on the features of the elements of the objects but treat them independently, whereas the Gromov-Wasserstein distance focuses only on the relations between the elements, depicting the structure of the object, yet discarding its features. In this paper we propose to extend these distances in order to encode simultaneously both the feature and structure informations, resulting in the Fused Gromov-Wasserstein distance. We develop the mathematical framework for this novel distance, prove its metric and interpolation properties and provide a concentration result for the convergence of finite samples. We also illustrate and interpret its use in various contexts where structured objects are involved.

From BOP to BOSS and Beyond: Time Series Classification with Dictionary Based Classifiers

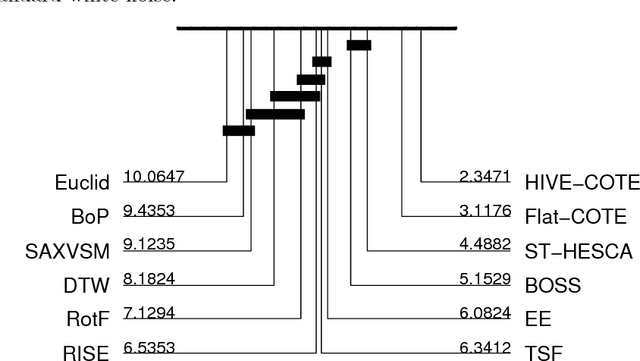
A family of algorithms for time series classification (TSC) involve running a sliding window across each series, discretising the window to form a word, forming a histogram of word counts over the dictionary, then constructing a classifier on the histograms. A recent evaluation of two of this type of algorithm, Bag of Patterns (BOP) and Bag of Symbolic Fourier Approximation Symbols (BOSS) found a significant difference in accuracy between these seemingly similar algorithms. We investigate this phenomenon by deconstructing the classifiers and measuring the relative importance of the four key components between BOP and BOSS. We find that whilst ensembling is a key component for both algorithms, the effect of the other components is mixed and more complex. We conclude that BOSS represents the state of the art for dictionary based TSC. Both BOP and BOSS can be classed as bag of words approaches. These are particularly popular in Computer Vision for tasks such as image classification. Converting approaches from vision requires careful engineering. We adapt three techniques used in Computer Vision for TSC: Scale Invariant Feature Transform; Spatial Pyramids; and Histrogram Intersection. We find that using Spatial Pyramids in conjunction with BOSS (SP) produces a significantly more accurate classifier. SP is significantly more accurate than standard benchmarks and the original BOSS algorithm. It is not significantly worse than the best shapelet based approach, and is only outperformed by HIVE-COTE, an ensemble that includes BOSS as a constituent module.

Optimal Transport for structured data

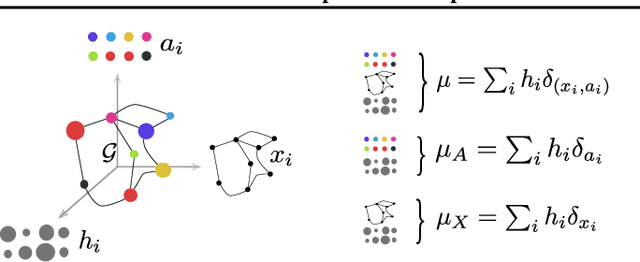
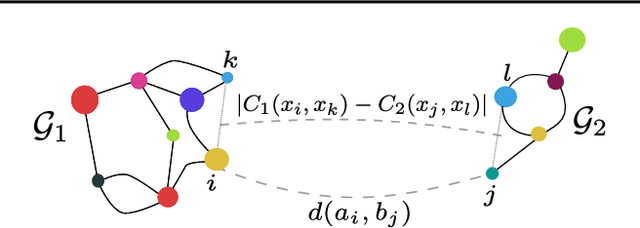
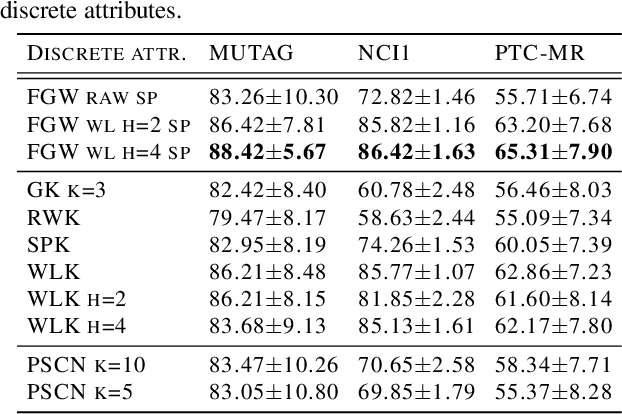
Optimal transport has recently gained a lot of interest in the machine learning community thanks to its ability to compare probability distributions while respecting the underlying space's geometry. Wasserstein distance deals with feature information through its metric or cost function, but fails in exploiting the structural information, i.e the specific relations existing among the components of the distribution. Recently adapted to a machine learning context, the Gromov-Wasserstein distance defines a metric well suited for comparing distributions that live in different metric spaces by exploiting their inner structural information. In this paper we propose a new optimal transport distance, called the Fused Gromov-Wasserstein distance, capable of leveraging both structural and feature information by combining both views and prove its metric properties over very general manifolds. We also define the barycenter of structured objects as their Fr\'echet mean, leveraging both feature and structural information. We illustrate the versatility of the method for problems where structured objects are involved, computing barycenters in graph and time series contexts. We also use this new distance for graph classification where we obtain comparable or superior results than state-of-the-art graph kernel methods and end-to-end graph CNN approach.

Dense Bag-of-Temporal-SIFT-Words for Time Series Classification

Time series classification is an application of particular interest with the increase of data to monitor. Classical techniques for time series classification rely on point-to-point distances. Recently, Bag-of-Words approaches have been used in this context. Words are quantized versions of simple features extracted from sliding windows. The SIFT framework has proved efficient for image classification. In this paper, we design a time series classification scheme that builds on the SIFT framework adapted to time series to feed a Bag-of-Words. We then refine our method by studying the impact of normalized Bag-of-Words, as well as densely extract point descriptors. Proposed adjustements achieve better performance. The evaluation shows that our method outperforms classical techniques in terms of classification.