Bridging Arbitrary and Tree Metrics via Differentiable Gromov Hyperbolicity

Trees and the associated shortest-path tree metrics provide a powerful framework for representing hierarchical and combinatorial structures in data. Given an arbitrary metric space, its deviation from a tree metric can be quantified by Gromov's $\delta$-hyperbolicity. Nonetheless, designing algorithms that bridge an arbitrary metric to its closest tree metric is still a vivid subject of interest, as most common approaches are either heuristical and lack guarantees, or perform moderately well. In this work, we introduce a novel differentiable optimization framework, coined DeltaZero, that solves this problem. Our method leverages a smooth surrogate for Gromov's $\delta$-hyperbolicity which enables a gradient-based optimization, with a tractable complexity. The corresponding optimization procedure is derived from a problem with better worst case guarantees than existing bounds, and is justified statistically. Experiments on synthetic and real-world datasets demonstrate that our method consistently achieves state-of-the-art distortion.

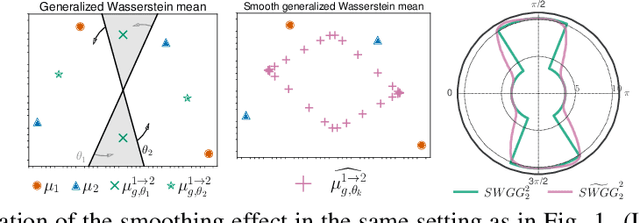
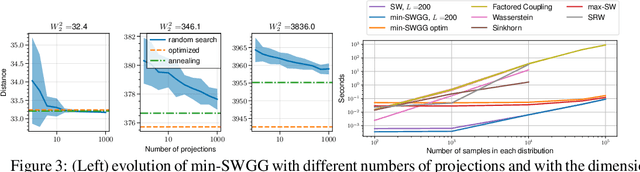
Differentiable Generalized Sliced Wasserstein Plans

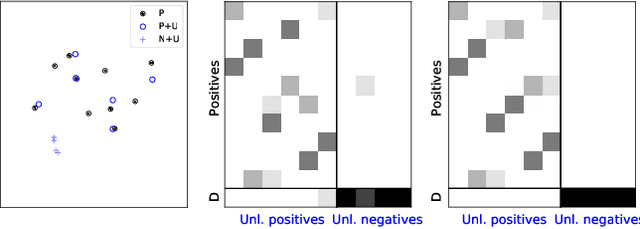
Optimal Transport (OT) has attracted significant interest in the machine learning community, not only for its ability to define meaningful distances between probability distributions -- such as the Wasserstein distance -- but also for its formulation of OT plans. Its computational complexity remains a bottleneck, though, and slicing techniques have been developed to scale OT to large datasets. Recently, a novel slicing scheme, dubbed min-SWGG, lifts a single one-dimensional plan back to the original multidimensional space, finally selecting the slice that yields the lowest Wasserstein distance as an approximation of the full OT plan. Despite its computational and theoretical advantages, min-SWGG inherits typical limitations of slicing methods: (i) the number of required slices grows exponentially with the data dimension, and (ii) it is constrained to linear projections. Here, we reformulate min-SWGG as a bilevel optimization problem and propose a differentiable approximation scheme to efficiently identify the optimal slice, even in high-dimensional settings. We furthermore define its generalized extension for accommodating to data living on manifolds. Finally, we demonstrate the practical value of our approach in various applications, including gradient flows on manifolds and high-dimensional spaces, as well as a novel sliced OT-based conditional flow matching for image generation -- where fast computation of transport plans is essential.

Match-And-Deform: Time Series Domain Adaptation through Optimal Transport and Temporal Alignment

While large volumes of unlabeled data are usually available, associated labels are often scarce. The unsupervised domain adaptation problem aims at exploiting labels from a source domain to classify data from a related, yet different, target domain. When time series are at stake, new difficulties arise as temporal shifts may appear in addition to the standard feature distribution shift. In this paper, we introduce the Match-And-Deform (MAD) approach that aims at finding correspondences between the source and target time series while allowing temporal distortions. The associated optimization problem simultaneously aligns the series thanks to an optimal transport loss and the time stamps through dynamic time warping. When embedded into a deep neural network, MAD helps learning new representations of time series that both align the domains and maximize the discriminative power of the network. Empirical studies on benchmark datasets and remote sensing data demonstrate that MAD makes meaningful sample-to-sample pairing and time shift estimation, reaching similar or better classification performance than state-of-the-art deep time series domain adaptation strategies.

Fast Optimal Transport through Sliced Wasserstein Generalized Geodesics

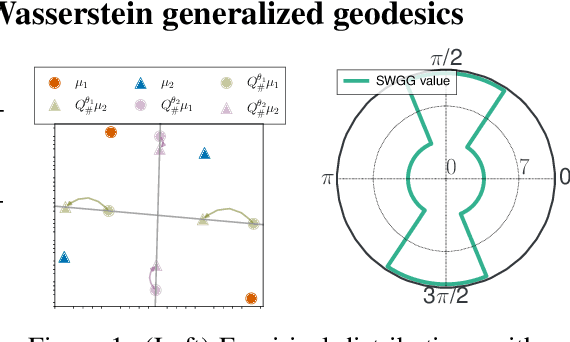
Wasserstein distance (WD) and the associated optimal transport plan have been proven useful in many applications where probability measures are at stake. In this paper, we propose a new proxy of the squared WD, coined min-SWGG, that is based on the transport map induced by an optimal one-dimensional projection of the two input distributions. We draw connections between min-SWGG and Wasserstein generalized geodesics in which the pivot measure is supported on a line. We notably provide a new closed form for the exact Wasserstein distance in the particular case of one of the distributions supported on a line allowing us to derive a fast computational scheme that is amenable to gradient descent optimization. We show that min-SWGG is an upper bound of WD and that it has a complexity similar to as Sliced-Wasserstein, with the additional feature of providing an associated transport plan. We also investigate some theoretical properties such as metricity, weak convergence, computational and topological properties. Empirical evidences support the benefits of min-SWGG in various contexts, from gradient flows, shape matching and image colorization, among others.

Hyperbolic Sliced-Wasserstein via Geodesic and Horospherical Projections

It has been shown beneficial for many types of data which present an underlying hierarchical structure to be embedded in hyperbolic spaces. Consequently, many tools of machine learning were extended to such spaces, but only few discrepancies to compare probability distributions defined over those spaces exist. Among the possible candidates, optimal transport distances are well defined on such Riemannian manifolds and enjoy strong theoretical properties, but suffer from high computational cost. On Euclidean spaces, sliced-Wasserstein distances, which leverage a closed-form of the Wasserstein distance in one dimension, are more computationally efficient, but are not readily available on hyperbolic spaces. In this work, we propose to derive novel hyperbolic sliced-Wasserstein discrepancies. These constructions use projections on the underlying geodesics either along horospheres or geodesics. We study and compare them on different tasks where hyperbolic representations are relevant, such as sampling or image classification.

Unbalanced Optimal Transport through Non-negative Penalized Linear Regression

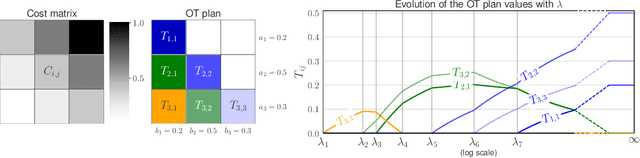
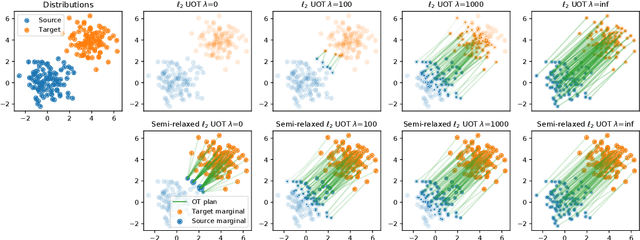
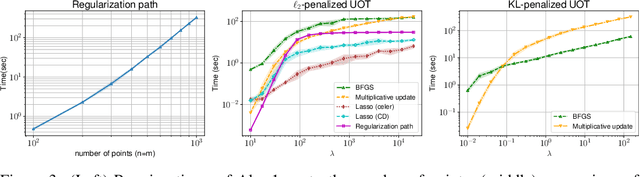
This paper addresses the problem of Unbalanced Optimal Transport (UOT) in which the marginal conditions are relaxed (using weighted penalties in lieu of equality) and no additional regularization is enforced on the OT plan. In this context, we show that the corresponding optimization problem can be reformulated as a non-negative penalized linear regression problem. This reformulation allows us to propose novel algorithms inspired from inverse problems and nonnegative matrix factorization. In particular, we consider majorization-minimization which leads in our setting to efficient multiplicative updates for a variety of penalties. Furthermore, we derive for the first time an efficient algorithm to compute the regularization path of UOT with quadratic penalties. The proposed algorithm provides a continuity of piece-wise linear OT plans converging to the solution of balanced OT (corresponding to infinite penalty weights). We perform several numerical experiments on simulated and real data illustrating the new algorithms, and provide a detailed discussion about more sophisticated optimization tools that can further be used to solve OT problems thanks to our reformulation.

Partial Gromov-Wasserstein with Applications on Positive-Unlabeled Learning

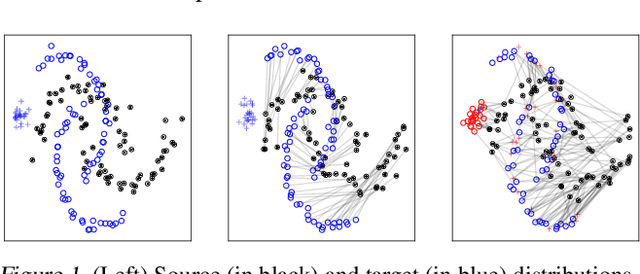
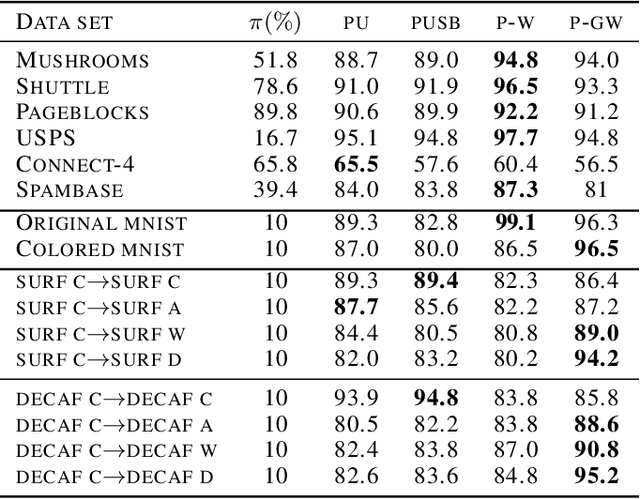
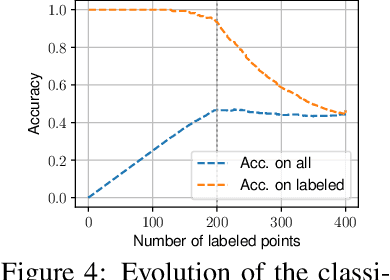
Optimal Transport (OT) framework allows defining similarity between probability distributions and provides metrics such as the Wasserstein and Gromov-Wasserstein discrepancies. Classical OT problem seeks a transportation map that preserves the total mass, requiring the mass of the source and target distributions to be the same. This may be too restrictive in certain applications such as color or shape matching, since the distributions may have arbitrary masses or that only a fraction of the total mass has to be transported. Several algorithms have been devised for computing unbalanced Wasserstein metrics but when it comes with the Gromov-Wasserstein problem, no partial formulation is available yet. This precludes from working with distributions that do not lie in the same metric space or when invariance to rotation or translation is needed. In this paper, we address the partial Gromov-Wasserstein problem and propose an algorithm to solve it. We showcase the new formulation in a positive-unlabeled (PU) learning application. To the best of our knowledge, this is the first application of optimal transport in this context and we first highlight that partial Wasserstein-based metrics prove effective in usual PU learning settings. We then demonstrate that partial Gromov-Wasserstein metrics is efficient in scenario where point clouds come from different domains or have different features.

Time Series Alignment with Global Invariances

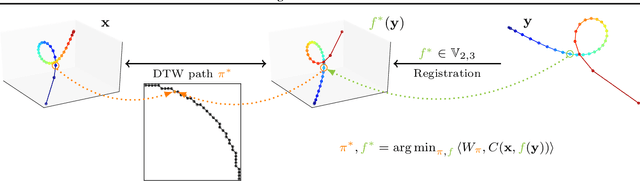
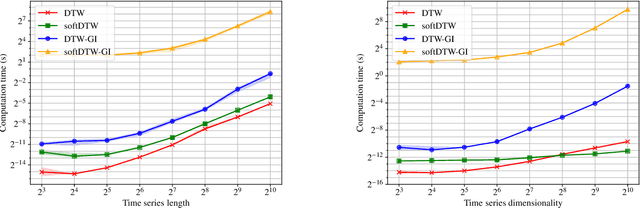
In this work we address the problem of comparing time series while taking into account both feature space transformation and temporal variability. The proposed framework combines a latent global transformation of the feature space with the widely used Dynamic Time Warping (DTW). The latent global transformation captures the feature invariance while the DTW (or its smooth counterpart soft-DTW) deals with the temporal shifts. We cast the problem as a joint optimization over the global transformation and the temporal alignments. The versatility of our framework allows for several variants depending on the invariance class at stake. Among our contributions we define a differentiable loss for time series and present two algorithms for the computation of time series barycenters under our new geometry. We illustrate the interest of our approach on both simulated and real world data.

Sliced Gromov-Wasserstein

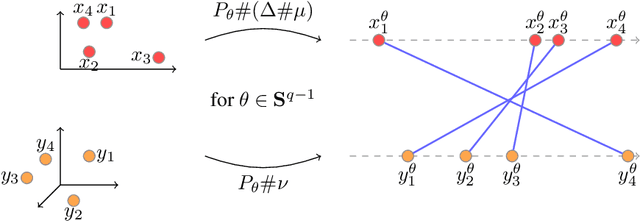
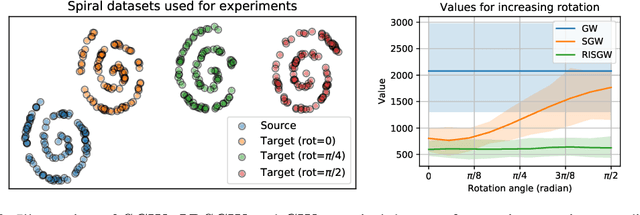
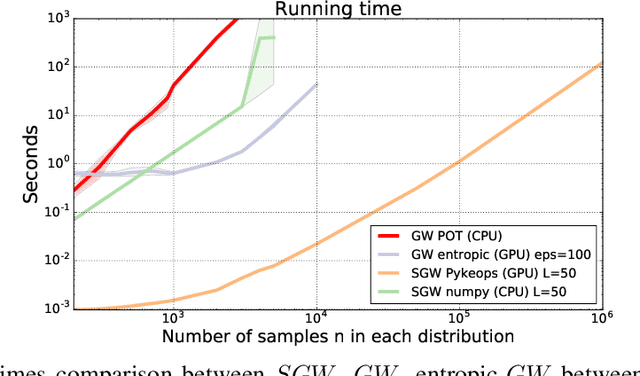
Recently used in various machine learning contexts, the Gromov-Wasserstein distance (GW) allows for comparing distributions that do not necessarily lie in the same metric space. However, this Optimal Transport (OT) distance requires solving a complex non convex quadratic program which is most of the time very costly both in time and memory. Contrary to GW, the Wasserstein distance (W) enjoys several properties (e.g. duality) that permit large scale optimization. Among those, the Sliced Wasserstein (SW) distance exploits the direct solution of W on the line, that only requires sorting discrete samples in 1D. This paper propose a new divergence based on GW akin to SW. We first derive a closed form for GW when dealing with 1D distributions, based on a new result for the related quadratic assignment problem. We then define a novel OT discrepancy that can deal with large scale distributions via a slicing approach and we show how it relates to the GW distance while being $O(n^2)$ to compute. We illustrate the behavior of this so called Sliced Gromov-Wasserstein (SGW) discrepancy in experiments where we demonstrate its ability to tackle similar problems as GW while being several order of magnitudes faster to compute

Optimal Transport for structured data

Optimal transport has recently gained a lot of interest in the machine learning community thanks to its ability to compare probability distributions while respecting the underlying space's geometry. Wasserstein distance deals with feature information through its metric or cost function, but fails in exploiting the structural information, i.e the specific relations existing among the components of the distribution. Recently adapted to a machine learning context, the Gromov-Wasserstein distance defines a metric well suited for comparing distributions that live in different metric spaces by exploiting their inner structural information. In this paper we propose a new optimal transport distance, called the Fused Gromov-Wasserstein distance, capable of leveraging both structural and feature information by combining both views and prove its metric properties over very general manifolds. We also define the barycenter of structured objects as their Fr\'echet mean, leveraging both feature and structural information. We illustrate the versatility of the method for problems where structured objects are involved, computing barycenters in graph and time series contexts. We also use this new distance for graph classification where we obtain comparable or superior results than state-of-the-art graph kernel methods and end-to-end graph CNN approach.