Bounds in Wasserstein distance for locally stationary processes

Locally stationary processes (LSPs) provide a robust framework for modeling time-varying phenomena, allowing for smooth variations in statistical properties such as mean and variance over time. In this paper, we address the estimation of the conditional probability distribution of LSPs using Nadaraya-Watson (NW) type estimators. The NW estimator approximates the conditional distribution of a target variable given covariates through kernel smoothing techniques. We establish the convergence rate of the NW conditional probability estimator for LSPs in the univariate setting under the Wasserstein distance and extend this analysis to the multivariate case using the sliced Wasserstein distance. Theoretical results are supported by numerical experiments on both synthetic and real-world datasets, demonstrating the practical usefulness of the proposed estimators.

Gaussian-Smoothed Sliced Probability Divergences

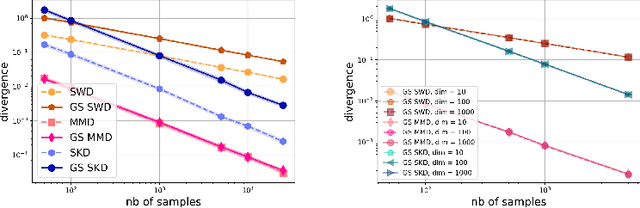
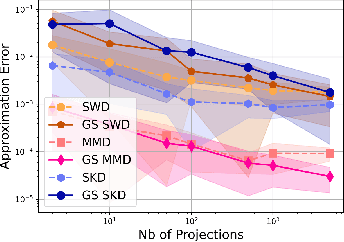
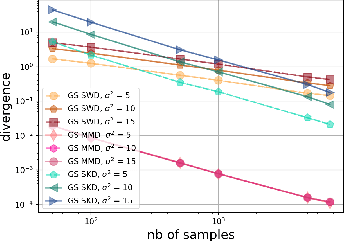
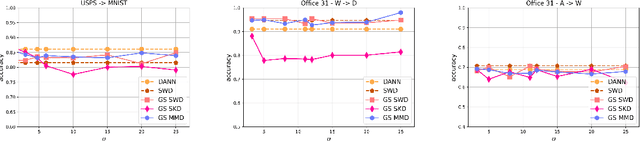
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown that it provides performances similar to its non-smoothed (non-private) counterpart. However, the computationaland statistical properties of such a metric have not yet been well-established. This work investigates the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian-smoothed sliced divergences. We first show that smoothing and slicing preserve the metric property and the weak topology. To study the sample complexity of such divergences, we then introduce $\hat{\hat\mu}_{n}$ the double empirical distribution for the smoothed-projected $\mu$. The distribution $\hat{\hat\mu}_{n}$ is a result of a double sampling process: one from sampling according to the origin distribution $\mu$ and the second according to the convolution of the projection of $\mu$ on the unit sphere and the Gaussian smoothing. We particularly focus on the Gaussian smoothed sliced Wasserstein distance and prove that it converges with a rate $O(n^{-1/2})$. We also derive other properties, including continuity, of different divergences with respect to the smoothing parameter. We support our theoretical findings with empirical studies in the context of privacy-preserving domain adaptation.

Adversarial Semi-Supervised Domain Adaptation for Semantic Segmentation: A New Role for Labeled Target Samples

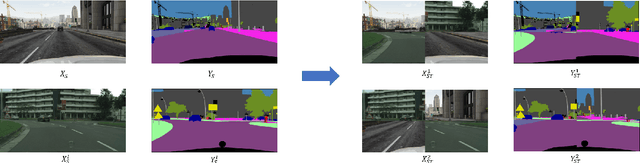
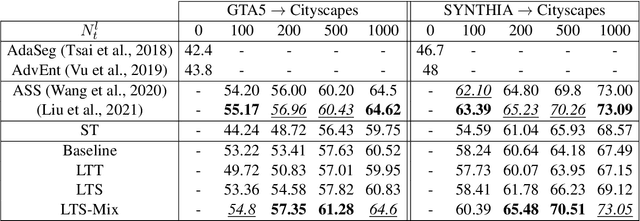
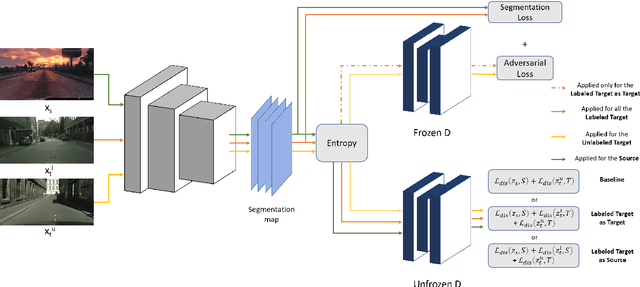
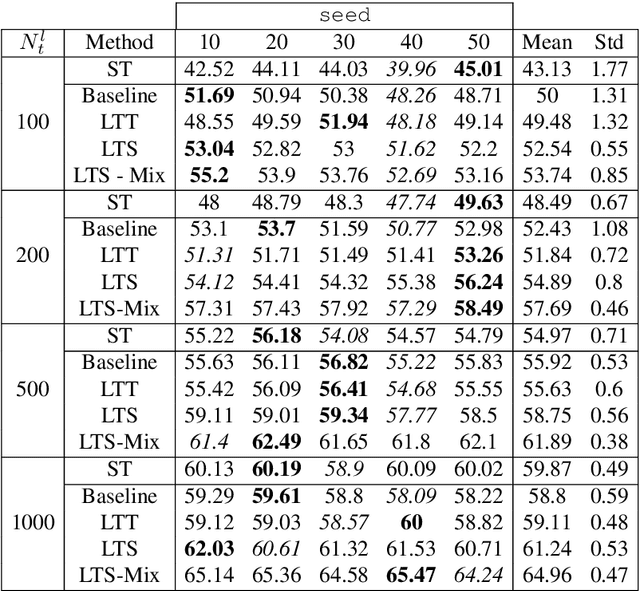
Adversarial learning baselines for domain adaptation (DA) approaches in the context of semantic segmentation are under explored in semi-supervised framework. These baselines involve solely the available labeled target samples in the supervision loss. In this work, we propose to enhance their usefulness on both semantic segmentation and the single domain classifier neural networks. We design new training objective losses for cases when labeled target data behave as source samples or as real target samples. The underlying rationale is that considering the set of labeled target samples as part of source domain helps reducing the domain discrepancy and, hence, improves the contribution of the adversarial loss. To support our approach, we consider a complementary method that mixes source and labeled target data, then applies the same adaptation process. We further propose an unsupervised selection procedure using entropy to optimize the choice of labeled target samples for adaptation. We illustrate our findings through extensive experiments on the benchmarks GTA5, SYNTHIA, and Cityscapes. The empirical evaluation highlights competitive performance of our proposed approach.

Statistical and Topological Properties of Gaussian Smoothed Sliced Probability Divergences

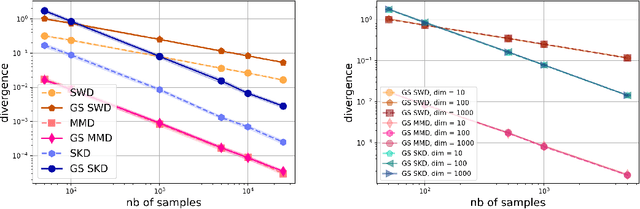
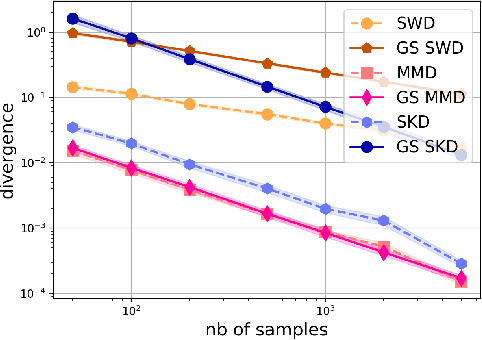
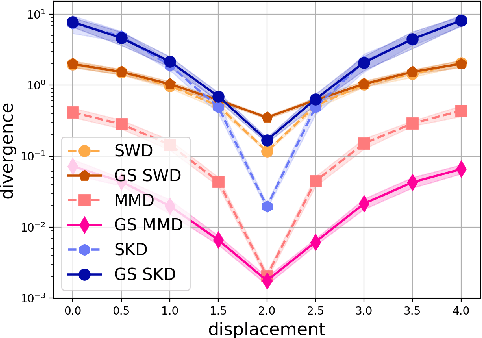
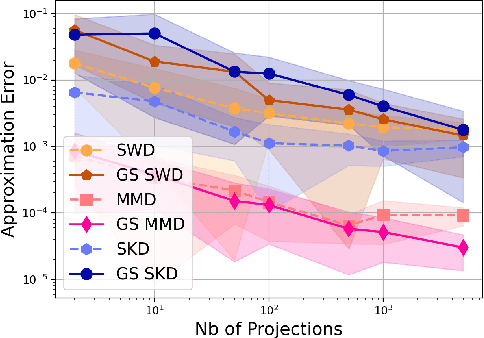
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown, in applications such as domain adaptation, to provide performances similar to its non-private (non-smoothed) counterpart. However, the computational and statistical properties of such a metric is not yet been well-established. In this paper, we analyze the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian smoothed sliced divergences. We show that smoothing and slicing preserve the metric property and the weak topology. We also provide results on the sample complexity of such divergences. Since, the privacy level depends on the amount of Gaussian smoothing, we analyze the impact of this parameter on the divergence. We support our theoretical findings with empirical studies of Gaussian smoothed and sliced version of Wassertein distance, Sinkhorn divergence and maximum mean discrepancy (MMD). In the context of privacy-preserving domain adaptation, we confirm that those Gaussian smoothed sliced Wasserstein and MMD divergences perform very well while ensuring data privacy.

Distributional Sliced Embedding Discrepancy for Incomparable Distributions

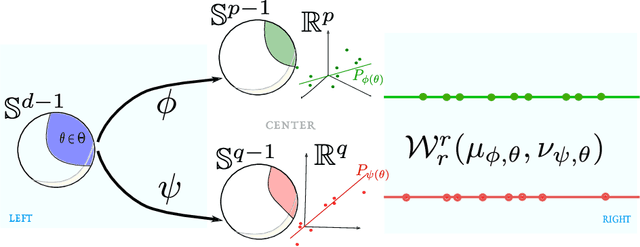
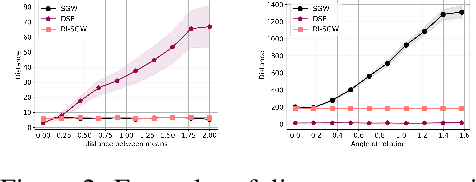
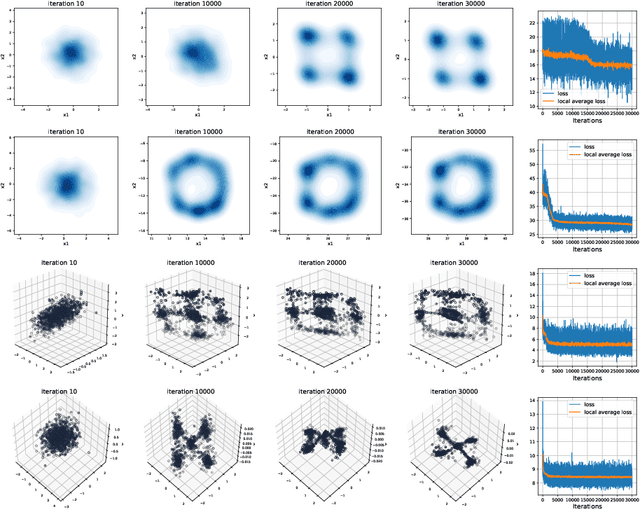
Gromov-Wasserstein (GW) distance is a key tool for manifold learning and cross-domain learning, allowing the comparison of distributions that do not live in the same metric space. Because of its high computational complexity, several approximate GW distances have been proposed based on entropy regularization or on slicing, and one-dimensional GW computation. In this paper, we propose a novel approach for comparing two incomparable distributions, that hinges on the idea of distributional slicing, embeddings, and on computing the closed-form Wasserstein distance between the sliced distributions. We provide a theoretical analysis of this new divergence, called distributional sliced embedding (DSE) discrepancy, and we show that it preserves several interesting properties of GW distance including rotation-invariance. We show that the embeddings involved in DSE can be efficiently learned. Finally, we provide a large set of experiments illustrating the behavior of DSE as a divergence in the context of generative modeling and in query framework.

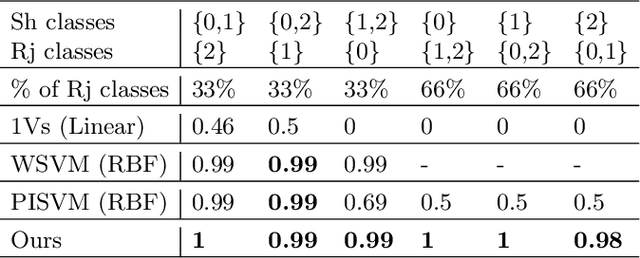
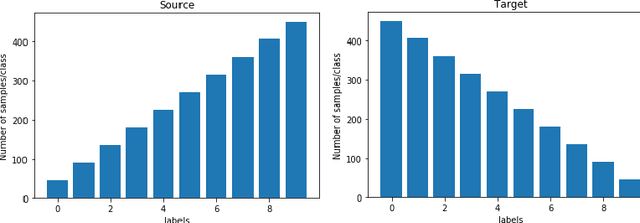
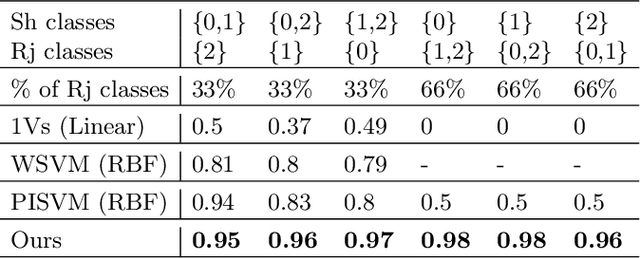
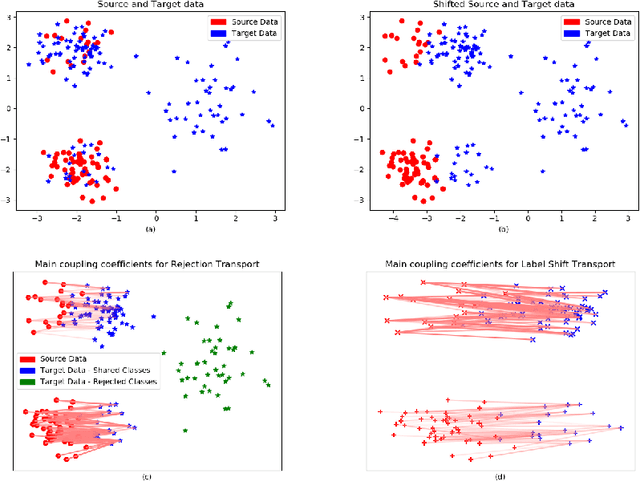
Open Set Domain Adaptation using Optimal Transport

We present a 2-step optimal transport approach that performs a mapping from a source distribution to a target distribution. Here, the target has the particularity to present new classes not present in the source domain. The first step of the approach aims at rejecting the samples issued from these new classes using an optimal transport plan. The second step solves the target (class ratio) shift still as an optimal transport problem. We develop a dual approach to solve the optimization problem involved at each step and we prove that our results outperform recent state-of-the-art performances. We further apply the approach to the setting where the source and target distributions present both a label-shift and an increasing covariate (features) shift to show its robustness.

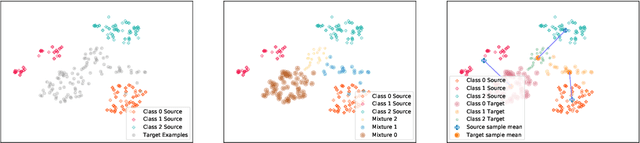
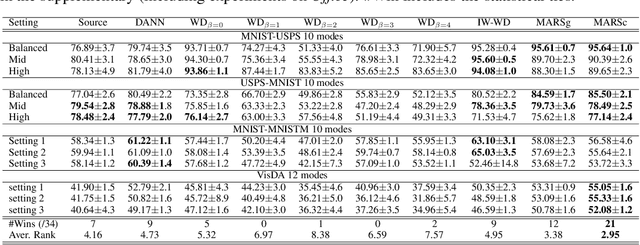
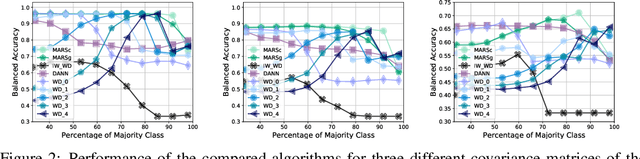
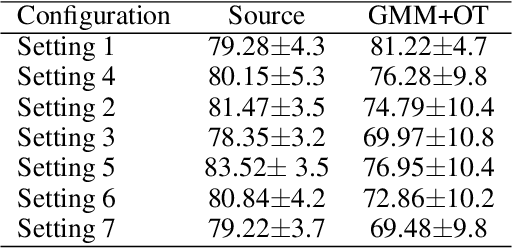
Match and Reweight Strategy for Generalized Target Shift

We address the problem of unsupervised domain adaptation under the setting of generalized target shift (both class-conditional and label shifts occur). We show that in that setting, for good generalization, it is necessary to learn with similar source and target label distributions and to match the class-conditional probabilities. For this purpose, we propose an estimation of target label proportion by blending mixture estimation and optimal transport. This estimation comes with theoretical guarantees of correctness. Based on the estimation, we learn a model by minimizing a importance weighted loss and a Wasserstein distance between weighted marginals. We prove that this minimization allows to match class-conditionals given mild assumptions on their geometry. Our experimental results show that our method performs better on average than competitors accross a range domain adaptation problems including digits,VisDA and Office.

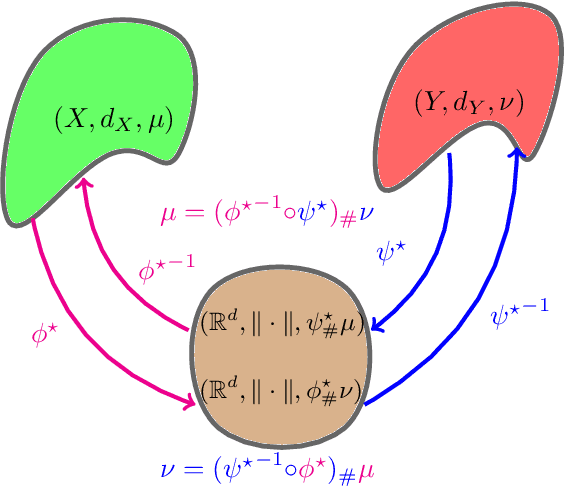
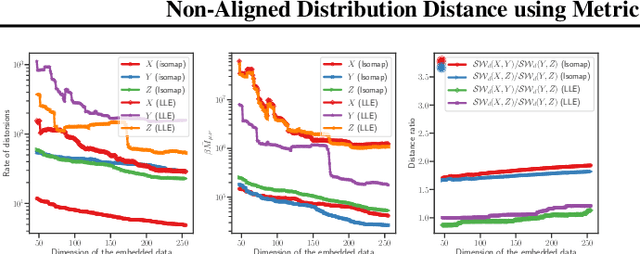
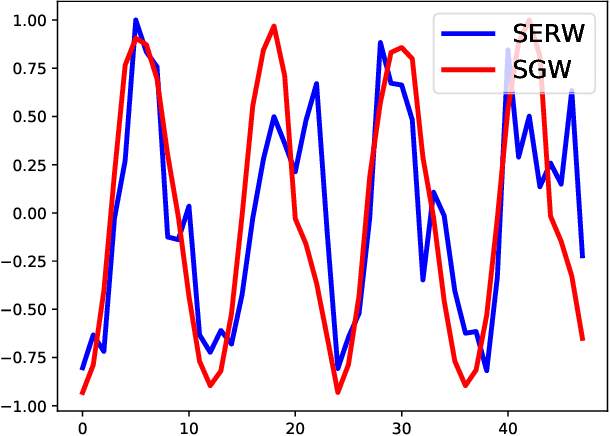
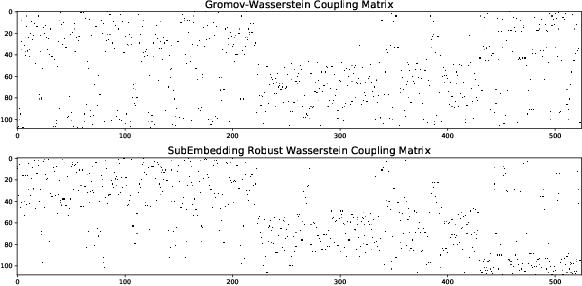
Non-Aligned Distribution Distance using Metric Measure Embedding and Optimal Transport

We propose a novel approach for comparing distributions whose supports do not necessarily lie on the same metric space. Unlike Gromov-Wasserstein (GW) distance that compares pairwise distance of elements from each distribution, we consider a method that embeds the metric measure spaces in a common Euclidean space and computes an optimal transport (OT) on the embedded distributions. This leads to what we call a sub-embedding robust Wasserstein(SERW). Under some conditions, SERW is a distance that considers an OT distance of the (low-distorted) embedded distributions using a common metric. In addition to this novel proposal that generalizes several recent OT works, our contributions stand on several theoretical analyses: i) we characterize the embedding spaces to define SERW distance for distribution alignment; ii) we prove that SERW mimics almost the same properties of GW distance, and we give a cost relation between GW and SERW. The paper also provides some numerical experiments illustrating how SERW behaves on matching problems in real-world.

Partial Gromov-Wasserstein with Applications on Positive-Unlabeled Learning

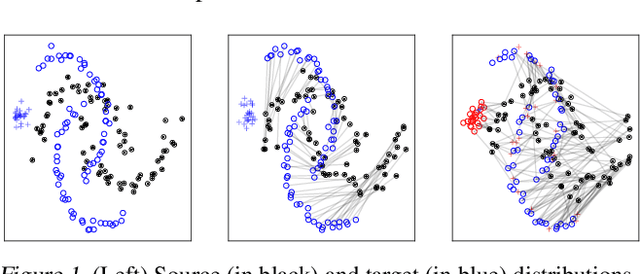
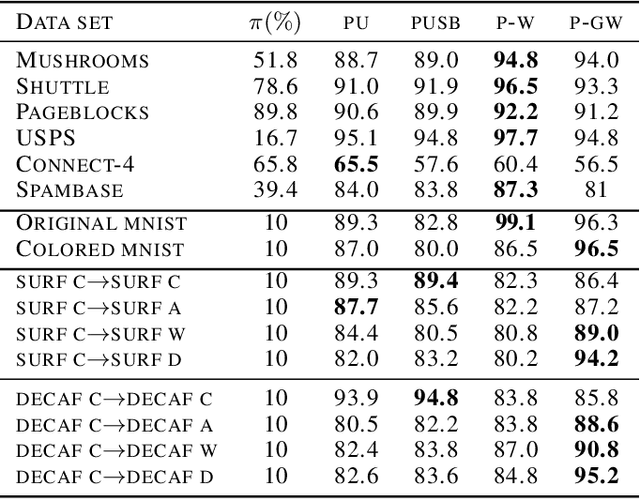
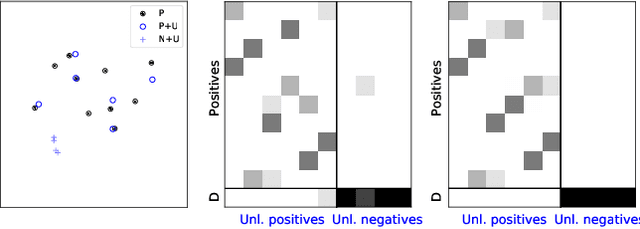
Optimal Transport (OT) framework allows defining similarity between probability distributions and provides metrics such as the Wasserstein and Gromov-Wasserstein discrepancies. Classical OT problem seeks a transportation map that preserves the total mass, requiring the mass of the source and target distributions to be the same. This may be too restrictive in certain applications such as color or shape matching, since the distributions may have arbitrary masses or that only a fraction of the total mass has to be transported. Several algorithms have been devised for computing unbalanced Wasserstein metrics but when it comes with the Gromov-Wasserstein problem, no partial formulation is available yet. This precludes from working with distributions that do not lie in the same metric space or when invariance to rotation or translation is needed. In this paper, we address the partial Gromov-Wasserstein problem and propose an algorithm to solve it. We showcase the new formulation in a positive-unlabeled (PU) learning application. To the best of our knowledge, this is the first application of optimal transport in this context and we first highlight that partial Wasserstein-based metrics prove effective in usual PU learning settings. We then demonstrate that partial Gromov-Wasserstein metrics is efficient in scenario where point clouds come from different domains or have different features.

Screening Sinkhorn Algorithm for Regularized Optimal Transport

We introduce in this paper a novel strategy for efficiently approximate the Sinkhorn distance between two discrete measures. After identifying neglectible components of the dual solution of the regularized Sinkhorn problem, we propose to screen those components by directly setting them at that value before entering the Sinkhorn problem. This allows us to solve a smaller Sinkhorn problem while ensuring approximation with provable guarantees. More formally, the approach is based on a reformulation of dual of Sinkhorn divergence problem and on the KKT optimality conditions of this problem, which enable identification of dual components to be screened. This new analysis leads to the Screenkhorn algorithm. We illustrate the efficiency of Screenkhorn on complex tasks such as dimensionality reduction or domain adaptation involving regularized optimal transport.