Universal Domain Adaptation Benchmark for Time Series Data Representation

Deep learning models have significantly improved the ability to detect novelties in time series (TS) data. This success is attributed to their strong representation capabilities. However, due to the inherent variability in TS data, these models often struggle with generalization and robustness. To address this, a common approach is to perform Unsupervised Domain Adaptation, particularly Universal Domain Adaptation (UniDA), to handle domain shifts and emerging novel classes. While extensively studied in computer vision, UniDA remains underexplored for TS data. This work provides a comprehensive implementation and comparison of state-of-the-art TS backbones in a UniDA framework. We propose a reliable protocol to evaluate their robustness and generalization across different domains. The goal is to provide practitioners with a framework that can be easily extended to incorporate future advancements in UniDA and TS architectures. Our results highlight the critical influence of backbone selection in UniDA performance and enable a robustness analysis across various datasets and architectures.

Optimal Transport and Adaptive Thresholding for Universal Domain Adaptation on Time Series

Universal Domain Adaptation (UniDA) aims to transfer knowledge from a labeled source domain to an unlabeled target domain, even when their classes are not fully shared. Few dedicated UniDA methods exist for Time Series (TS), which remains a challenging case. In general, UniDA approaches align common class samples and detect unknown target samples from emerging classes. Such detection often results from thresholding a discriminability metric. The threshold value is typically either a fine-tuned hyperparameter or a fixed value, which limits the ability of the model to adapt to new data. Furthermore, discriminability metrics exhibit overconfidence for unknown samples, leading to misclassifications. This paper introduces UniJDOT, an optimal-transport-based method that accounts for the unknown target samples in the transport cost. Our method also proposes a joint decision space to improve the discriminability of the detection module. In addition, we use an auto-thresholding algorithm to reduce the dependence on fixed or fine-tuned thresholds. Finally, we rely on a Fourier transform-based layer inspired by the Fourier Neural Operator for better TS representation. Experiments on TS benchmarks demonstrate the discriminability, robustness, and state-of-the-art performance of UniJDOT.

Gaussian-Smoothed Sliced Probability Divergences

Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown that it provides performances similar to its non-smoothed (non-private) counterpart. However, the computationaland statistical properties of such a metric have not yet been well-established. This work investigates the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian-smoothed sliced divergences. We first show that smoothing and slicing preserve the metric property and the weak topology. To study the sample complexity of such divergences, we then introduce $\hat{\hat\mu}_{n}$ the double empirical distribution for the smoothed-projected $\mu$. The distribution $\hat{\hat\mu}_{n}$ is a result of a double sampling process: one from sampling according to the origin distribution $\mu$ and the second according to the convolution of the projection of $\mu$ on the unit sphere and the Gaussian smoothing. We particularly focus on the Gaussian smoothed sliced Wasserstein distance and prove that it converges with a rate $O(n^{-1/2})$. We also derive other properties, including continuity, of different divergences with respect to the smoothing parameter. We support our theoretical findings with empirical studies in the context of privacy-preserving domain adaptation.

Stochastic gradient descent with gradient estimator for categorical features

Categorical data are present in key areas such as health or supply chain, and this data require specific treatment. In order to apply recent machine learning models on such data, encoding is needed. In order to build interpretable models, one-hot encoding is still a very good solution, but such encoding creates sparse data. Gradient estimators are not suited for sparse data: the gradient is mainly considered as zero while it simply does not always exists, thus a novel gradient estimator is introduced. We show what this estimator minimizes in theory and show its efficiency on different datasets with multiple model architectures. This new estimator performs better than common estimators under similar settings. A real world retail dataset is also released after anonymization. Overall, the aim of this paper is to thoroughly consider categorical data and adapt models and optimizers to these key features.

Statistical and Topological Properties of Gaussian Smoothed Sliced Probability Divergences

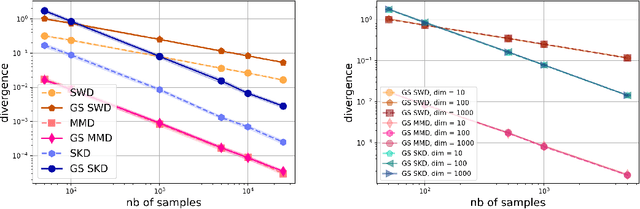
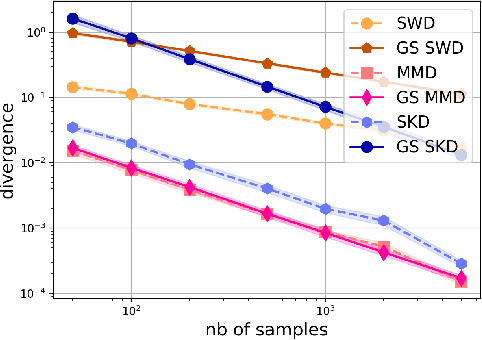
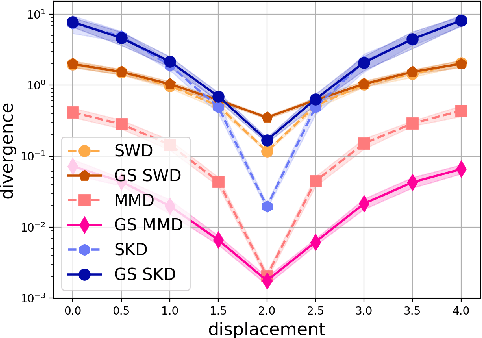
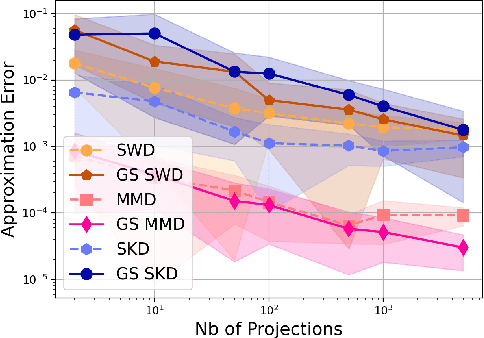
Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown, in applications such as domain adaptation, to provide performances similar to its non-private (non-smoothed) counterpart. However, the computational and statistical properties of such a metric is not yet been well-established. In this paper, we analyze the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian smoothed sliced divergences. We show that smoothing and slicing preserve the metric property and the weak topology. We also provide results on the sample complexity of such divergences. Since, the privacy level depends on the amount of Gaussian smoothing, we analyze the impact of this parameter on the divergence. We support our theoretical findings with empirical studies of Gaussian smoothed and sliced version of Wassertein distance, Sinkhorn divergence and maximum mean discrepancy (MMD). In the context of privacy-preserving domain adaptation, we confirm that those Gaussian smoothed sliced Wasserstein and MMD divergences perform very well while ensuring data privacy.

Distributional Sliced Embedding Discrepancy for Incomparable Distributions

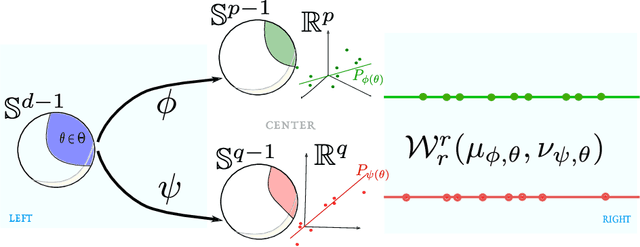
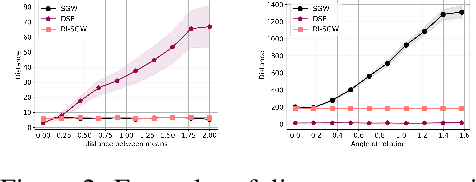
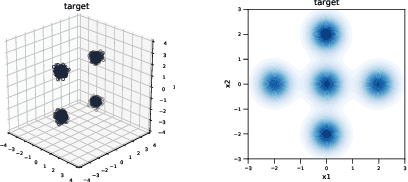
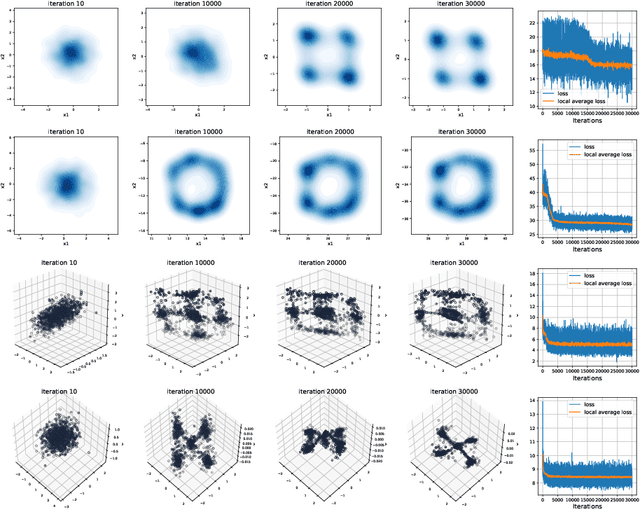
Gromov-Wasserstein (GW) distance is a key tool for manifold learning and cross-domain learning, allowing the comparison of distributions that do not live in the same metric space. Because of its high computational complexity, several approximate GW distances have been proposed based on entropy regularization or on slicing, and one-dimensional GW computation. In this paper, we propose a novel approach for comparing two incomparable distributions, that hinges on the idea of distributional slicing, embeddings, and on computing the closed-form Wasserstein distance between the sliced distributions. We provide a theoretical analysis of this new divergence, called distributional sliced embedding (DSE) discrepancy, and we show that it preserves several interesting properties of GW distance including rotation-invariance. We show that the embeddings involved in DSE can be efficiently learned. Finally, we provide a large set of experiments illustrating the behavior of DSE as a divergence in the context of generative modeling and in query framework.

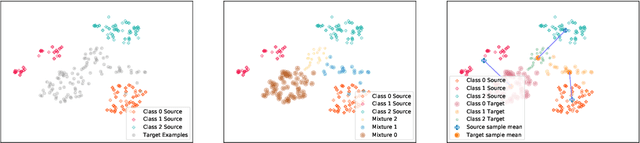
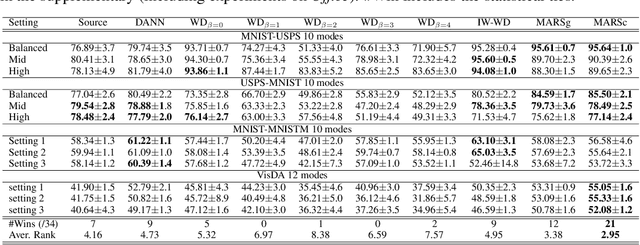
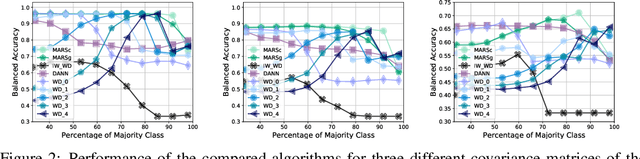
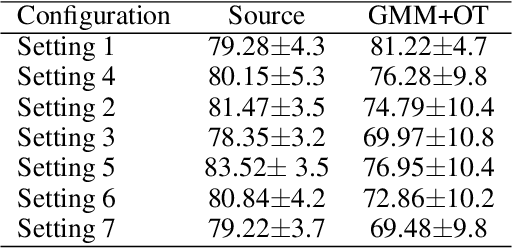
Match and Reweight Strategy for Generalized Target Shift

We address the problem of unsupervised domain adaptation under the setting of generalized target shift (both class-conditional and label shifts occur). We show that in that setting, for good generalization, it is necessary to learn with similar source and target label distributions and to match the class-conditional probabilities. For this purpose, we propose an estimation of target label proportion by blending mixture estimation and optimal transport. This estimation comes with theoretical guarantees of correctness. Based on the estimation, we learn a model by minimizing a importance weighted loss and a Wasserstein distance between weighted marginals. We prove that this minimization allows to match class-conditionals given mild assumptions on their geometry. Our experimental results show that our method performs better on average than competitors accross a range domain adaptation problems including digits,VisDA and Office.

Wasserstein Distance Measure Machines

This paper presents a distance-based discriminative framework for learning with probability distributions. Instead of using kernel mean embeddings or generalized radial basis kernels, we introduce embeddings based on dissimilarity of distributions to some reference distributions denoted as templates. Our framework extends the theory of similarity of \citet{balcan2008theory} to the population distribution case and we prove that, for some learning problems, Wasserstein distance achieves low-error linear decision functions with high probability. Our key result is to prove that the theory also holds for empirical distributions. Algorithmically, the proposed approach is very simple as it consists in computing a mapping based on pairwise Wasserstein distances and then learning a linear decision function. Our experimental results show that this Wasserstein distance embedding performs better than kernel mean embeddings and computing Wasserstein distance is far more tractable than estimating pairwise Kullback-Leibler divergence of empirical distributions.

Adaptive Canonical Correlation Analysis Based On Matrix Manifolds

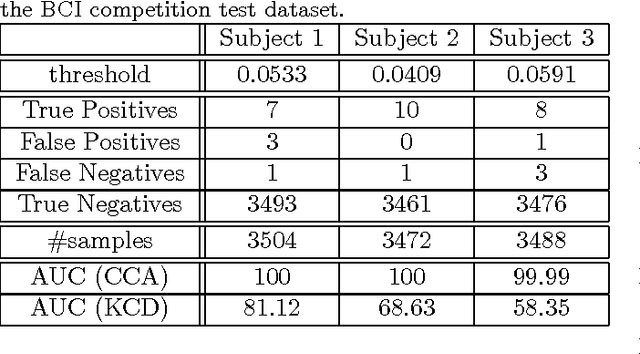
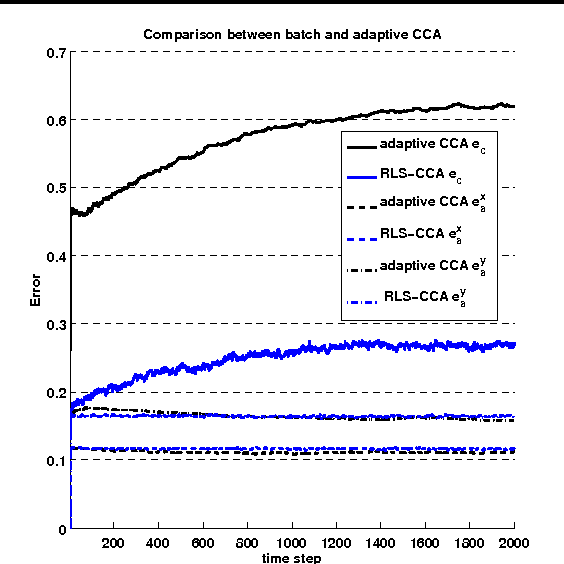
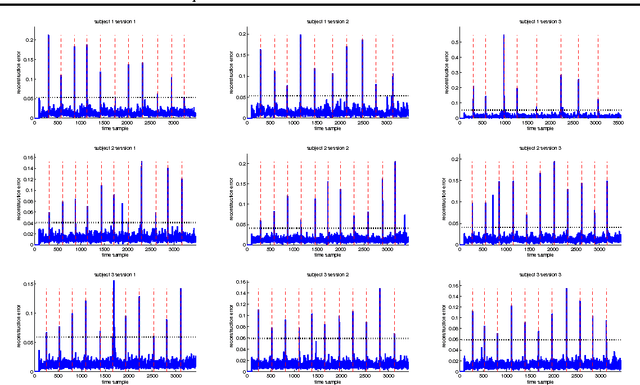
In this paper, we formulate the Canonical Correlation Analysis (CCA) problem on matrix manifolds. This framework provides a natural way for dealing with matrix constraints and tools for building efficient algorithms even in an adaptive setting. Finally, an adaptive CCA algorithm is proposed and applied to a change detection problem in EEG signals.

Craniofacial reconstruction as a prediction problem using a Latent Root Regression model

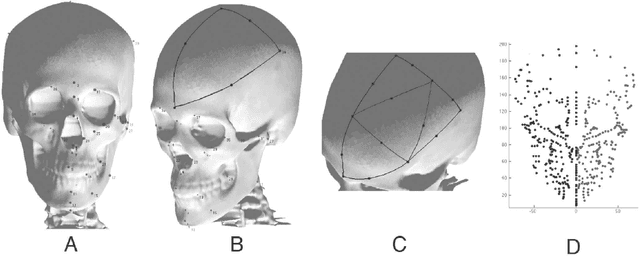
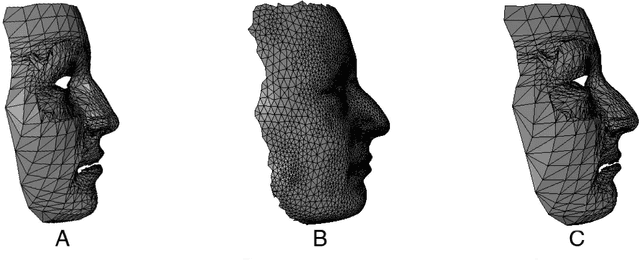
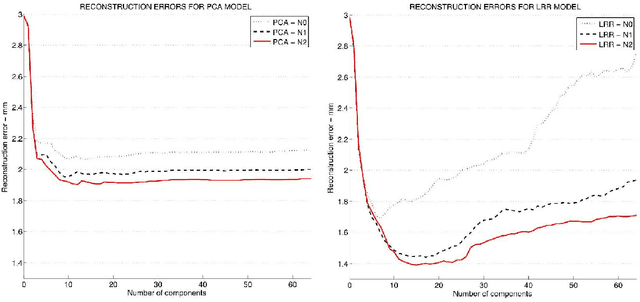
In this paper, we present a computer-assisted method for facial reconstruction. This method provides an estimation of the facial shape associated with unidentified skeletal remains. Current computer-assisted methods using a statistical framework rely on a common set of extracted points located on the bone and soft-tissue surfaces. Most of the facial reconstruction methods then consist of predicting the position of the soft-tissue surface points, when the positions of the bone surface points are known. We propose to use Latent Root Regression for prediction. The results obtained are then compared to those given by Principal Components Analysis linear models. In conjunction, we have evaluated the influence of the number of skull landmarks used. Anatomical skull landmarks are completed iteratively by points located upon geodesics which link these anatomical landmarks, thus enabling us to artificially increase the number of skull points. Facial points are obtained using a mesh-matching algorithm between a common reference mesh and individual soft-tissue surface meshes. The proposed method is validated in term of accuracy, based on a leave-one-out cross-validation test applied to a homogeneous database. Accuracy measures are obtained by computing the distance between the original face surface and its reconstruction. Finally, these results are discussed referring to current computer-assisted reconstruction facial techniques.