Giga-scale Kernel Matrix Vector Multiplication on GPU

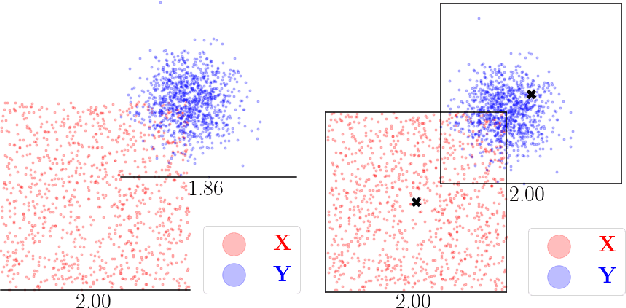
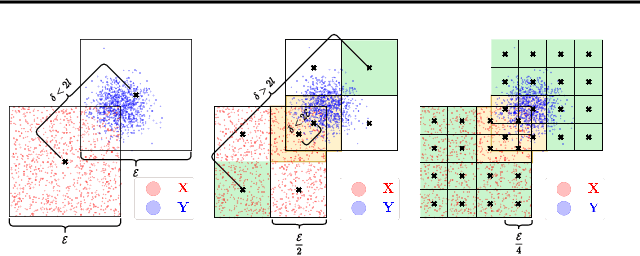
Kernel matrix vector multiplication (KMVM) is a ubiquitous operation in machine learning and scientific computing, spanning from the kernel literature to signal processing. As kernel matrix vector multiplication tends to scale quadratically in both memory and time, applications are often limited by these computational scaling constraints. We propose a novel approximation procedure coined Faster-Fast and Free Memory Method ($\text{F}^3$M) to address these scaling issues for KMVM. Extensive experiments demonstrate that $\text{F}^3$M has empirical \emph{linear time and memory} complexity with a relative error of order $10^{-3}$ and can compute a full KMVM for a billion points \emph{in under one minute} on a high-end GPU, leading to a significant speed-up in comparison to existing CPU methods. We further demonstrate the utility of our procedure by applying it as a drop-in for the state-of-the-art GPU-based linear solver FALKON, \emph{improving speed 3-5 times} at the cost of $<$1\% drop in accuracy.

Kernel Operations on the GPU, with Autodiff, without Memory Overflows

The KeOps library provides a fast and memory-efficient GPU support for tensors whose entries are given by a mathematical formula, such as kernel and distance matrices. KeOps alleviates the major bottleneck of tensor-centric libraries for kernel and geometric applications: memory consumption. It also supports automatic differentiation and outperforms standard GPU baselines, including PyTorch CUDA tensors or the Halide and TVM libraries. KeOps combines optimized C++/CUDA schemes with binders for high-level languages: Python (Numpy and PyTorch), Matlab and GNU R. As a result, high-level "quadratic" codes can now scale up to large data sets with millions of samples processed in seconds. KeOps brings graphics-like performances for kernel methods and is freely available on standard repositories (PyPi, CRAN). To showcase its versatility, we provide tutorials in a wide range of settings online at \url{www.kernel-operations.io}.

Craniofacial reconstruction as a prediction problem using a Latent Root Regression model

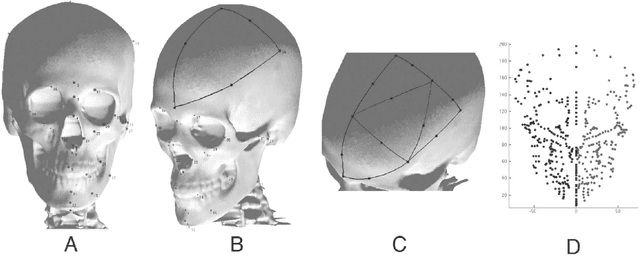
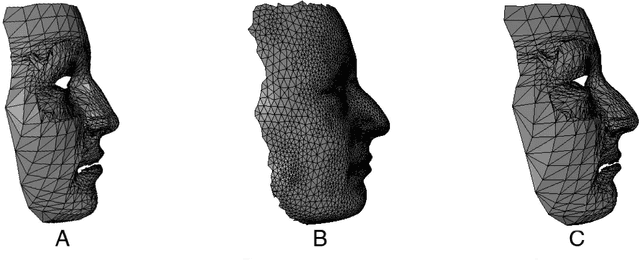
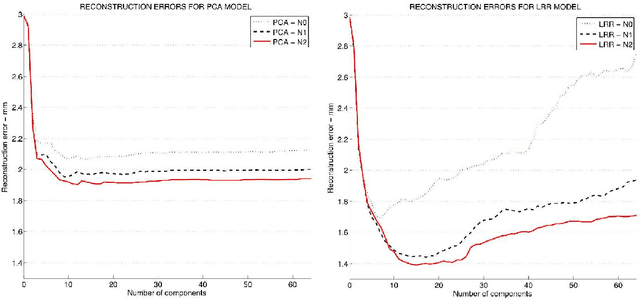
In this paper, we present a computer-assisted method for facial reconstruction. This method provides an estimation of the facial shape associated with unidentified skeletal remains. Current computer-assisted methods using a statistical framework rely on a common set of extracted points located on the bone and soft-tissue surfaces. Most of the facial reconstruction methods then consist of predicting the position of the soft-tissue surface points, when the positions of the bone surface points are known. We propose to use Latent Root Regression for prediction. The results obtained are then compared to those given by Principal Components Analysis linear models. In conjunction, we have evaluated the influence of the number of skull landmarks used. Anatomical skull landmarks are completed iteratively by points located upon geodesics which link these anatomical landmarks, thus enabling us to artificially increase the number of skull points. Facial points are obtained using a mesh-matching algorithm between a common reference mesh and individual soft-tissue surface meshes. The proposed method is validated in term of accuracy, based on a leave-one-out cross-validation test applied to a homogeneous database. Accuracy measures are obtained by computing the distance between the original face surface and its reconstruction. Finally, these results are discussed referring to current computer-assisted reconstruction facial techniques.