Cooperative learning of Pl@ntNet's Artificial Intelligence algorithm: how does it work and how can we improve it?

Deep learning models for plant species identification rely on large annotated datasets. The PlantNet system enables global data collection by allowing users to upload and annotate plant observations, leading to noisy labels due to diverse user skills. Achieving consensus is crucial for training, but the vast scale of collected data makes traditional label aggregation strategies challenging. Existing methods either retain all observations, resulting in noisy training data or selectively keep those with sufficient votes, discarding valuable information. Additionally, as many species are rarely observed, user expertise can not be evaluated as an inter-user agreement: otherwise, botanical experts would have a lower weight in the AI training step than the average user. Our proposed label aggregation strategy aims to cooperatively train plant identification AI models. This strategy estimates user expertise as a trust score per user based on their ability to identify plant species from crowdsourced data. The trust score is recursively estimated from correctly identified species given the current estimated labels. This interpretable score exploits botanical experts' knowledge and the heterogeneity of users. Subsequently, our strategy removes unreliable observations but retains those with limited trusted annotations, unlike other approaches. We evaluate PlantNet's strategy on a released large subset of the PlantNet database focused on European flora, comprising over 6M observations and 800K users. We demonstrate that estimating users' skills based on the diversity of their expertise enhances labeling performance. Our findings emphasize the synergy of human annotation and data filtering in improving AI performance for a refined dataset. We explore incorporating AI-based votes alongside human input. This can further enhance human-AI interactions to detect unreliable observations.

Improve learning combining crowdsourced labels by weighting Areas Under the Margin

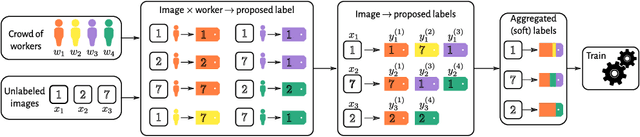
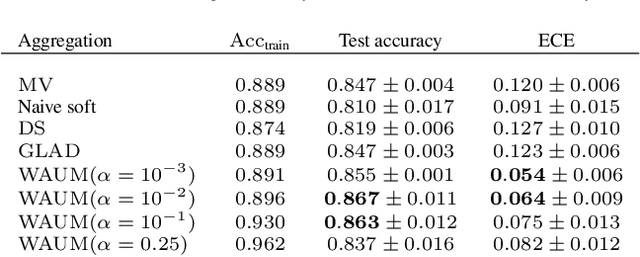
In supervised learning -- for instance in image classification -- modern massive datasets are commonly labeled by a crowd of workers. The obtained labels in this crowdsourcing setting are then aggregated for training. The aggregation step generally leverages a per worker trust score. Yet, such worker-centric approaches discard each task ambiguity. Some intrinsically ambiguous tasks might even fool expert workers, which could eventually be harmful for the learning step. In a standard supervised learning setting -- with one label per task and balanced classes -- the Area Under the Margin (AUM) statistic is tailored to identify mislabeled data. We adapt the AUM to identify ambiguous tasks in crowdsourced learning scenarios, introducing the Weighted AUM (WAUM). The WAUM is an average of AUMs weighted by worker and task dependent scores. We show that the WAUM can help discarding ambiguous tasks from the training set, leading to better generalization or calibration performance. We report improvements with respect to feature-blind aggregation strategies both for simulated settings and for the CIFAR-10H crowdsourced dataset.

Benchopt: Reproducible, efficient and collaborative optimization benchmarks

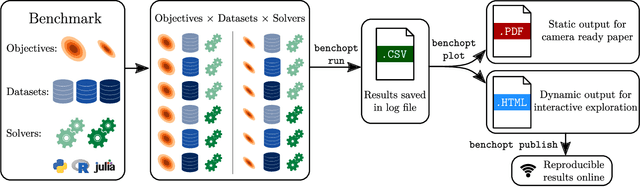
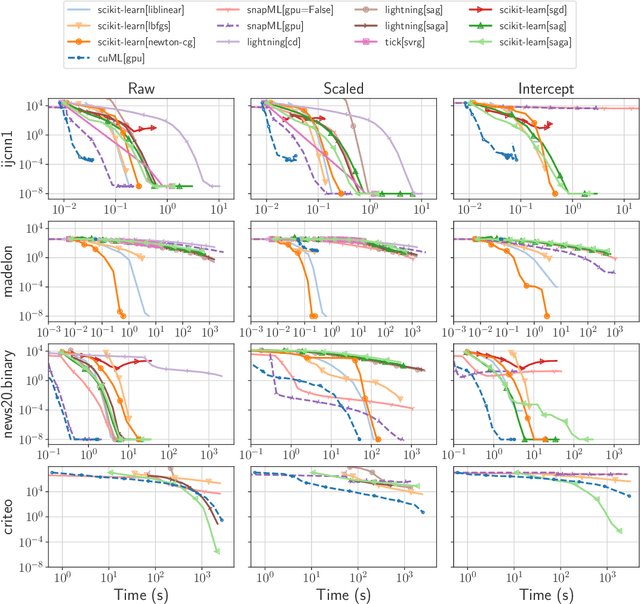
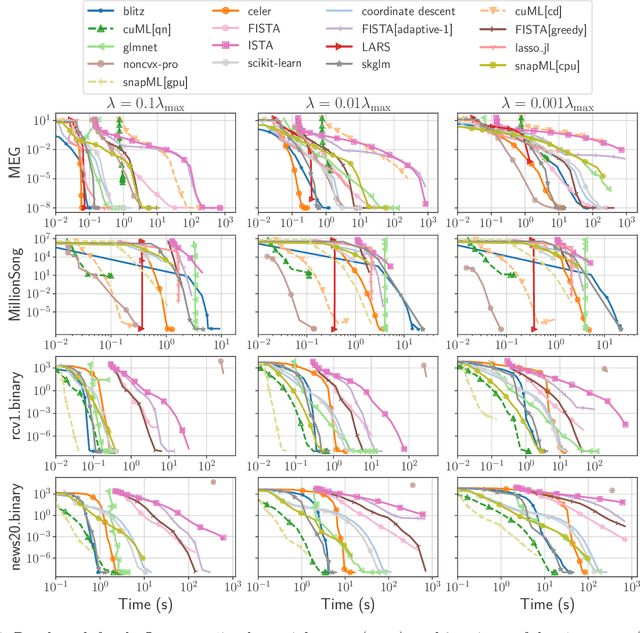
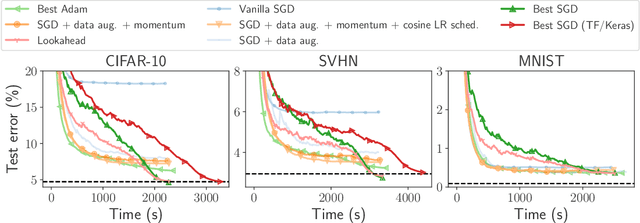
Numerical validation is at the core of machine learning research as it allows to assess the actual impact of new methods, and to confirm the agreement between theory and practice. Yet, the rapid development of the field poses several challenges: researchers are confronted with a profusion of methods to compare, limited transparency and consensus on best practices, as well as tedious re-implementation work. As a result, validation is often very partial, which can lead to wrong conclusions that slow down the progress of research. We propose Benchopt, a collaborative framework to automate, reproduce and publish optimization benchmarks in machine learning across programming languages and hardware architectures. Benchopt simplifies benchmarking for the community by providing an off-the-shelf tool for running, sharing and extending experiments. To demonstrate its broad usability, we showcase benchmarks on three standard learning tasks: $\ell_2$-regularized logistic regression, Lasso, and ResNet18 training for image classification. These benchmarks highlight key practical findings that give a more nuanced view of the state-of-the-art for these problems, showing that for practical evaluation, the devil is in the details. We hope that Benchopt will foster collaborative work in the community hence improving the reproducibility of research findings.

Kernel Operations on the GPU, with Autodiff, without Memory Overflows

The KeOps library provides a fast and memory-efficient GPU support for tensors whose entries are given by a mathematical formula, such as kernel and distance matrices. KeOps alleviates the major bottleneck of tensor-centric libraries for kernel and geometric applications: memory consumption. It also supports automatic differentiation and outperforms standard GPU baselines, including PyTorch CUDA tensors or the Halide and TVM libraries. KeOps combines optimized C++/CUDA schemes with binders for high-level languages: Python (Numpy and PyTorch), Matlab and GNU R. As a result, high-level "quadratic" codes can now scale up to large data sets with millions of samples processed in seconds. KeOps brings graphics-like performances for kernel methods and is freely available on standard repositories (PyPi, CRAN). To showcase its versatility, we provide tutorials in a wide range of settings online at \url{www.kernel-operations.io}.

Parallel transport in shape analysis: a scalable numerical scheme

The analysis of manifold-valued data requires efficient tools from Riemannian geometry to cope with the computational complexity at stake. This complexity arises from the always-increasing dimension of the data, and the absence of closed-form expressions to basic operations such as the Riemannian logarithm. In this paper, we adapt a generic numerical scheme recently introduced for computing parallel transport along geodesics in a Riemannian manifold to finite-dimensional manifolds of diffeomorphisms. We provide a qualitative and quantitative analysis of its behavior on high-dimensional manifolds, and investigate an application with the prediction of brain structures progression.

Prediction of the progression of subcortical brain structures in Alzheimer's disease from baseline

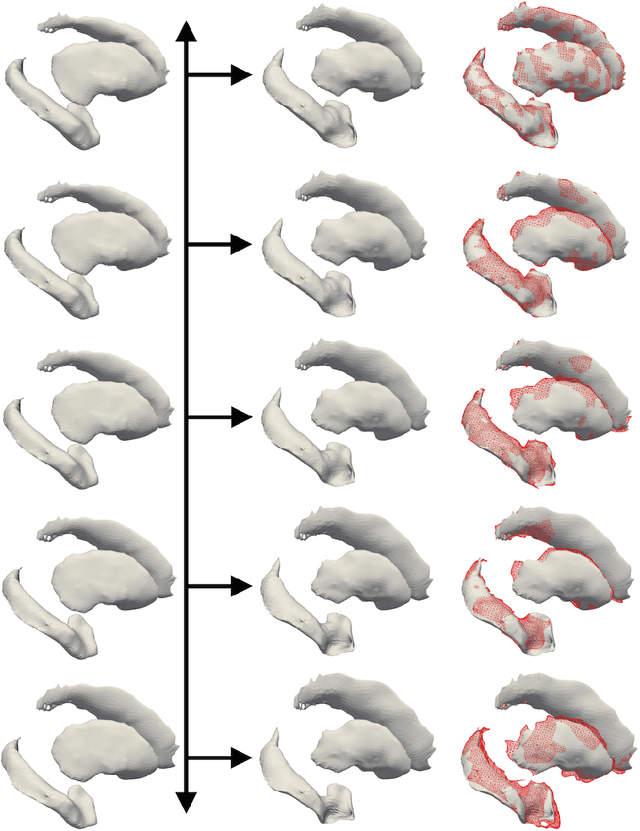
We propose a method to predict the subject-specific longitudinal progression of brain structures extracted from baseline MRI, and evaluate its performance on Alzheimer's disease data. The disease progression is modeled as a trajectory on a group of diffeomorphisms in the context of large deformation diffeomorphic metric mapping (LDDMM). We first exhibit the limited predictive abilities of geodesic regression extrapolation on this group. Building on the recent concept of parallel curves in shape manifolds, we then introduce a second predictive protocol which personalizes previously learned trajectories to new subjects, and investigate the relative performances of two parallel shifting paradigms. This design only requires the baseline imaging data. Finally, coefficients encoding the disease dynamics are obtained from longitudinal cognitive measurements for each subject, and exploited to refine our methodology which is demonstrated to successfully predict the follow-up visits.

White Matter Fiber Segmentation Using Functional Varifolds

The extraction of fibers from dMRI data typically produces a large number of fibers, it is common to group fibers into bundles. To this end, many specialized distance measures, such as MCP, have been used for fiber similarity. However, these distance based approaches require point-wise correspondence and focus only on the geometry of the fibers. Recent publications have highlighted that using microstructure measures along fibers improves tractography analysis. Also, many neurodegenerative diseases impacting white matter require the study of microstructure measures as well as the white matter geometry. Motivated by these, we propose to use a novel computational model for fibers, called functional varifolds, characterized by a metric that considers both the geometry and microstructure measure (e.g. GFA) along the fiber pathway. We use it to cluster fibers with a dictionary learning and sparse coding-based framework, and present a preliminary analysis using HCP data.

The fshape framework for the variability analysis of functional shapes

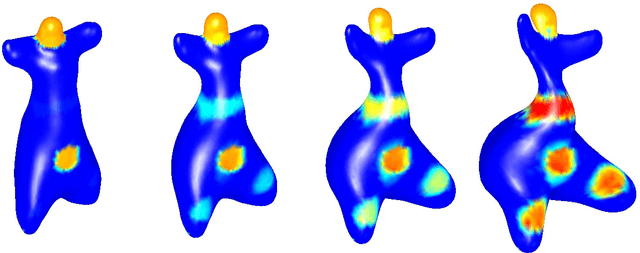
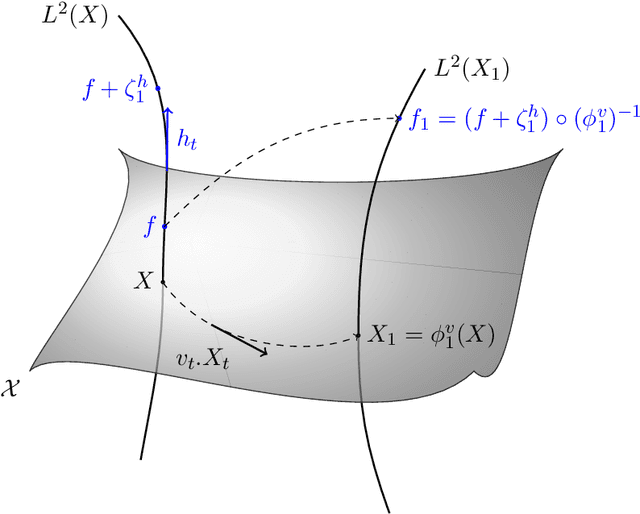
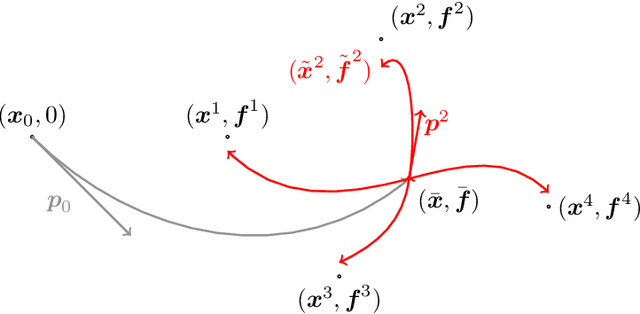
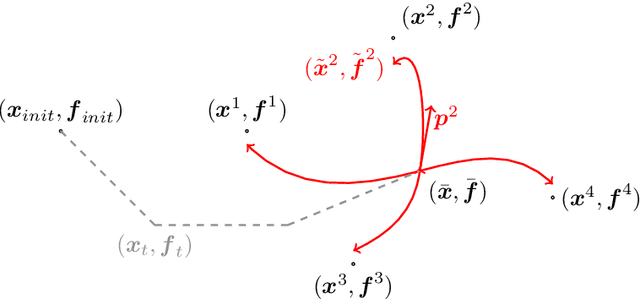
This article introduces a full mathematical and numerical framework for treating functional shapes (or fshapes) following the landmarks of shape spaces and shape analysis. Functional shapes can be described as signal functions supported on varying geometrical supports. Analysing variability of fshapes' ensembles require the modelling and quantification of joint variations in geometry and signal, which have been treated separately in previous approaches. Instead, building on the ideas of shape spaces for purely geometrical objects, we propose the extended concept of fshape bundles and define Riemannian metrics for fshape metamorphoses to model geometrico-functional transformations within these bundles. We also generalize previous works on data attachment terms based on the notion of varifolds and demonstrate the utility of these distances. Based on these, we propose variational formulations of the atlas estimation problem on populations of fshapes and prove existence of solutions for the different models. The second part of the article examines the numerical implementation of the models by detailing discrete expressions for the metrics and gradients and proposing an optimization scheme for the atlas estimation problem. We present a few results of the methodology on a synthetic dataset as well as on a population of retinal membranes with thickness maps.