Schur's Positive-Definite Network: Deep Learning in the SPD cone with structure

Estimating matrices in the symmetric positive-definite (SPD) cone is of interest for many applications ranging from computer vision to graph learning. While there exist various convex optimization-based estimators, they remain limited in expressivity due to their model-based approach. The success of deep learning has thus led many to use neural networks to learn to estimate SPD matrices in a data-driven fashion. For learning structured outputs, one promising strategy involves architectures designed by unrolling iterative algorithms, which potentially benefit from inductive bias properties. However, designing correct unrolled architectures for SPD learning is difficult: they either do not guarantee that their output has all the desired properties, rely on heavy computations, or are overly restrained to specific matrices which hinders their expressivity. In this paper, we propose a novel and generic learning module with guaranteed SPD outputs called SpodNet, that also enables learning a larger class of functions than existing approaches. Notably, it solves the challenging task of learning jointly SPD and sparse matrices. Our experiments demonstrate the versatility of SpodNet layers.

Implicit Differentiation for Hyperparameter Tuning the Weighted Graphical Lasso

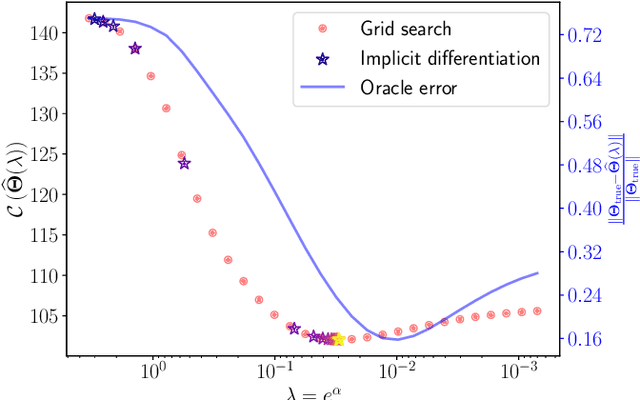
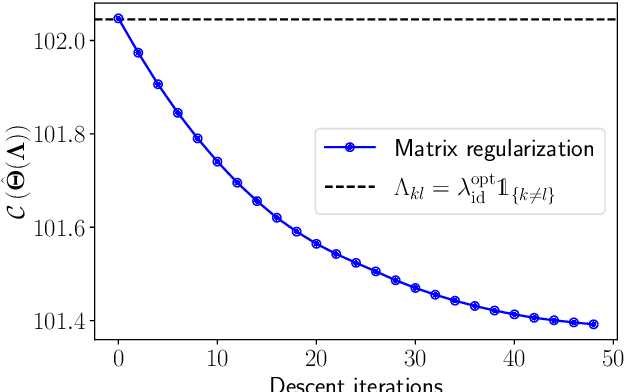
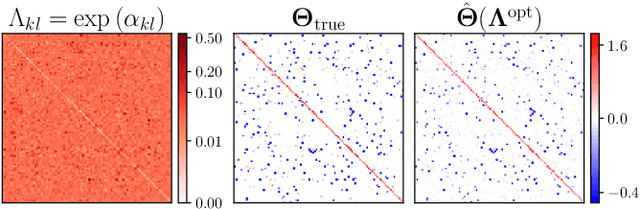
We provide a framework and algorithm for tuning the hyperparameters of the Graphical Lasso via a bilevel optimization problem solved with a first-order method. In particular, we derive the Jacobian of the Graphical Lasso solution with respect to its regularization hyperparameters.

Coordinate Descent for SLOPE

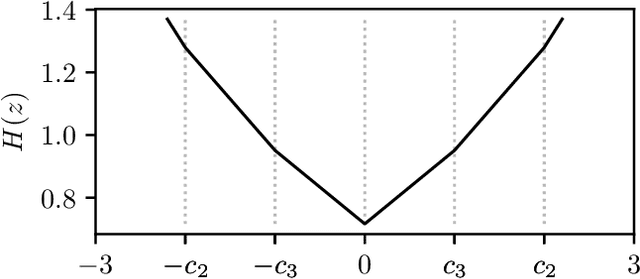
The lasso is the most famous sparse regression and feature selection method. One reason for its popularity is the speed at which the underlying optimization problem can be solved. Sorted L-One Penalized Estimation (SLOPE) is a generalization of the lasso with appealing statistical properties. In spite of this, the method has not yet reached widespread interest. A major reason for this is that current software packages that fit SLOPE rely on algorithms that perform poorly in high dimensions. To tackle this issue, we propose a new fast algorithm to solve the SLOPE optimization problem, which combines proximal gradient descent and proximal coordinate descent steps. We provide new results on the directional derivative of the SLOPE penalty and its related SLOPE thresholding operator, as well as provide convergence guarantees for our proposed solver. In extensive benchmarks on simulated and real data, we show that our method outperforms a long list of competing algorithms.

Benchopt: Reproducible, efficient and collaborative optimization benchmarks

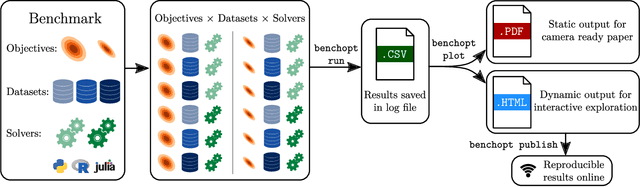
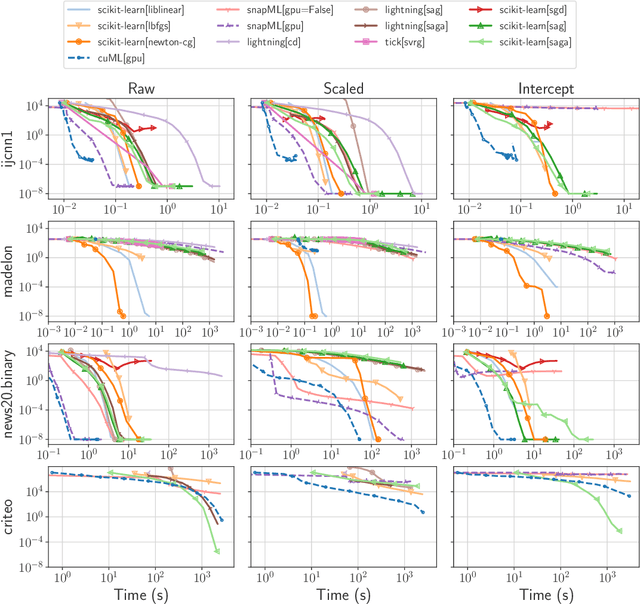
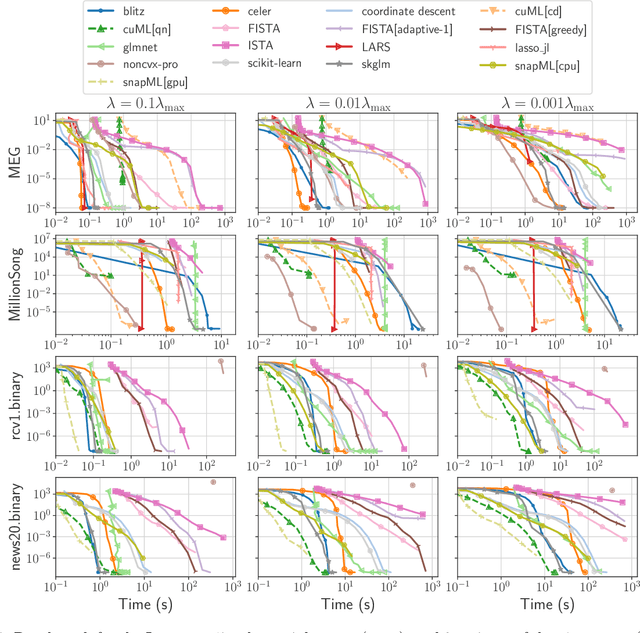
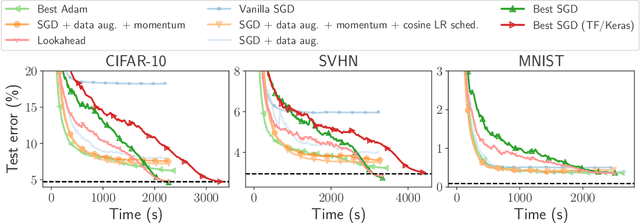
Numerical validation is at the core of machine learning research as it allows to assess the actual impact of new methods, and to confirm the agreement between theory and practice. Yet, the rapid development of the field poses several challenges: researchers are confronted with a profusion of methods to compare, limited transparency and consensus on best practices, as well as tedious re-implementation work. As a result, validation is often very partial, which can lead to wrong conclusions that slow down the progress of research. We propose Benchopt, a collaborative framework to automate, reproduce and publish optimization benchmarks in machine learning across programming languages and hardware architectures. Benchopt simplifies benchmarking for the community by providing an off-the-shelf tool for running, sharing and extending experiments. To demonstrate its broad usability, we showcase benchmarks on three standard learning tasks: $\ell_2$-regularized logistic regression, Lasso, and ResNet18 training for image classification. These benchmarks highlight key practical findings that give a more nuanced view of the state-of-the-art for these problems, showing that for practical evaluation, the devil is in the details. We hope that Benchopt will foster collaborative work in the community hence improving the reproducibility of research findings.

Beyond L1: Faster and Better Sparse Models with skglm

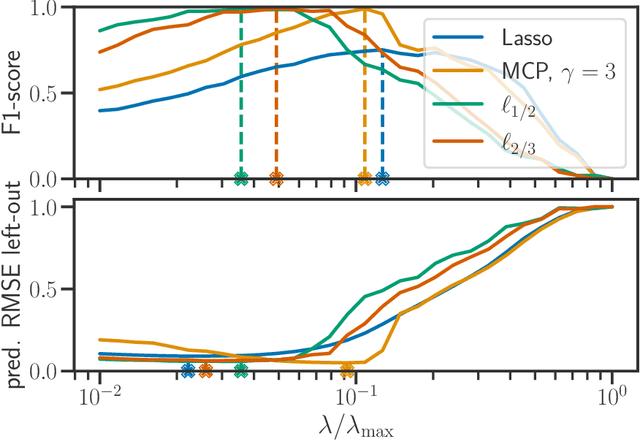
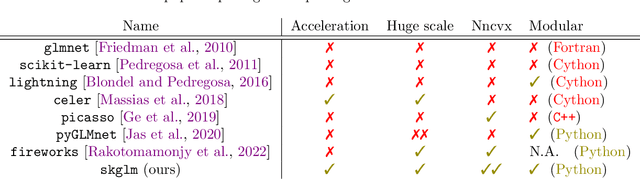
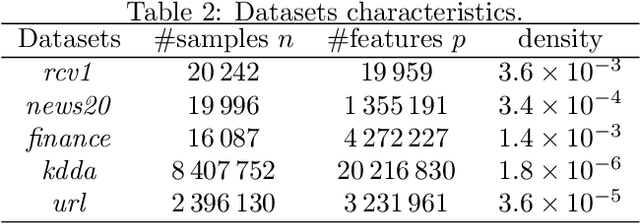
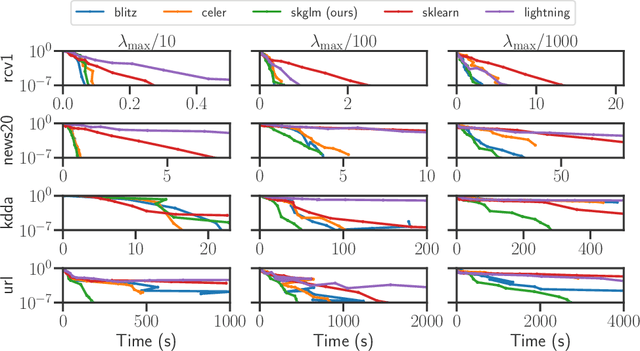
We propose a new fast algorithm to estimate any sparse generalized linear model with convex or non-convex separable penalties. Our algorithm is able to solve problems with millions of samples and features in seconds, by relying on coordinate descent, working sets and Anderson acceleration. It handles previously unaddressed models, and is extensively shown to improve state-of-art algorithms. We provide a flexible, scikit-learn compatible package, which easily handles customized datafits and penalties.

Iterative regularization for low complexity regularizers

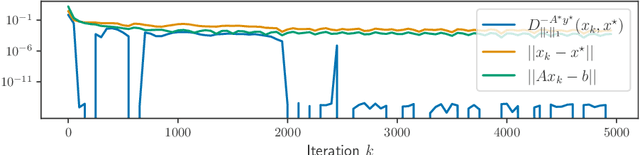
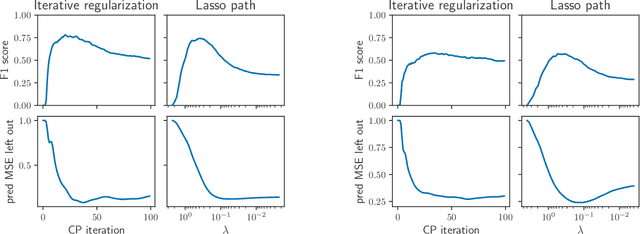
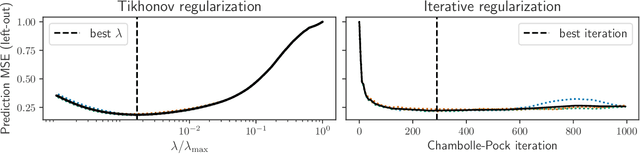
Iterative regularization exploits the implicit bias of an optimization algorithm to regularize ill-posed problems. Constructing algorithms with such built-in regularization mechanisms is a classic challenge in inverse problems but also in modern machine learning, where it provides both a new perspective on algorithms analysis, and significant speed-ups compared to explicit regularization. In this work, we propose and study the first iterative regularization procedure able to handle biases described by non smooth and non strongly convex functionals, prominent in low-complexity regularization. Our approach is based on a primal-dual algorithm of which we analyze convergence and stability properties, even in the case where the original problem is unfeasible. The general results are illustrated considering the special case of sparse recovery with the $\ell_1$ penalty. Our theoretical results are complemented by experiments showing the computational benefits of our approach.

Implicit differentiation for fast hyperparameter selection in non-smooth convex learning

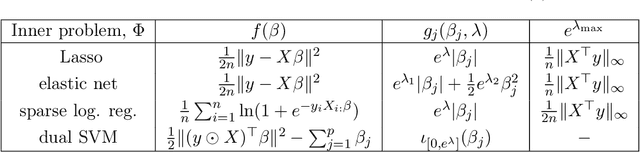
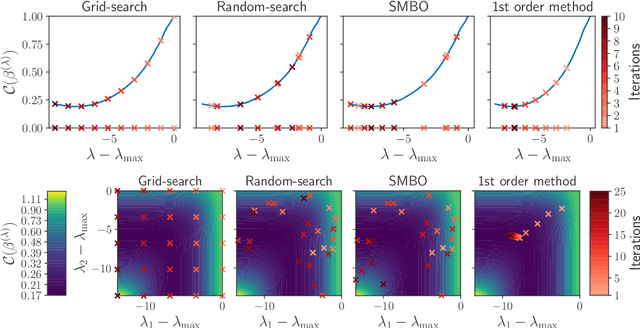
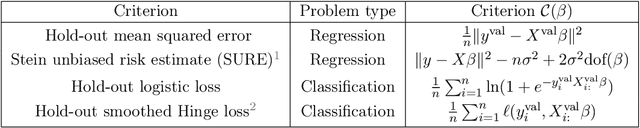
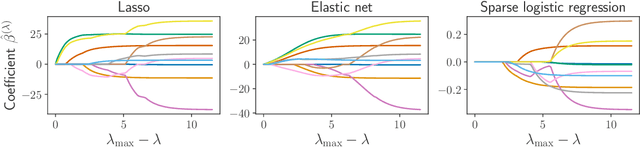
Finding the optimal hyperparameters of a model can be cast as a bilevel optimization problem, typically solved using zero-order techniques. In this work we study first-order methods when the inner optimization problem is convex but non-smooth. We show that the forward-mode differentiation of proximal gradient descent and proximal coordinate descent yield sequences of Jacobians converging toward the exact Jacobian. Using implicit differentiation, we show it is possible to leverage the non-smoothness of the inner problem to speed up the computation. Finally, we provide a bound on the error made on the hypergradient when the inner optimization problem is solved approximately. Results on regression and classification problems reveal computational benefits for hyperparameter optimization, especially when multiple hyperparameters are required.

Anderson acceleration of coordinate descent

Acceleration of first order methods is mainly obtained via inertial techniques \`a la Nesterov, or via nonlinear extrapolation. The latter has known a recent surge of interest, with successful applications to gradient and proximal gradient techniques. On multiple Machine Learning problems, coordinate descent achieves performance significantly superior to full-gradient methods. Speeding up coordinate descent in practice is not easy: inertially accelerated versions of coordinate descent are theoretically accelerated, but might not always lead to practical speed-ups. We propose an accelerated version of coordinate descent using extrapolation, showing considerable speed up in practice, compared to inertial accelerated coordinate descent and extrapolated (proximal) gradient descent. Experiments on least squares, Lasso, elastic net and logistic regression validate the approach.

Implicit regularization for convex regularizers

We study implicit regularization for over-parameterized linear models, when the bias is convex but not necessarily strongly convex. We characterize the regularization property of a primal-dual gradient based approach, analyzing convergence and especially stability in the presence of worst case deterministic noise. As a main example, we specialize and illustrate the results for the problem of robust sparse recovery. Key to our analysis is a combination of ideas from regularization theory and optimization in the presence of errors. Theoretical results are complemented by experiments showing that state-of-the-art performances are achieved with considerable computational speed-ups.

Dimension-free convergence rates for gradient Langevin dynamics in RKHS

Gradient Langevin dynamics (GLD) and stochastic GLD (SGLD) have attracted considerable attention lately, as a way to provide convergence guarantees in a non-convex setting. However, the known rates grow exponentially with the dimension of the space. In this work, we provide a convergence analysis of GLD and SGLD when the optimization space is an infinite dimensional Hilbert space. More precisely, we derive non-asymptotic, dimension-free convergence rates for GLD/SGLD when performing regularized non-convex optimization in a reproducing kernel Hilbert space. Amongst others, the convergence analysis relies on the properties of a stochastic differential equation, its discrete time Galerkin approximation and the geometric ergodicity of the associated Markov chains.