Compressive Recovery of Sparse Precision Matrices

We consider the problem of learning a graph modeling the statistical relations of the $d$ variables of a dataset with $n$ samples $X \in \mathbb{R}^{n \times d}$. Standard approaches amount to searching for a precision matrix $\Theta$ representative of a Gaussian graphical model that adequately explains the data. However, most maximum likelihood-based estimators usually require storing the $d^{2}$ values of the empirical covariance matrix, which can become prohibitive in a high-dimensional setting. In this work, we adopt a compressive viewpoint and aim to estimate a sparse $\Theta$ from a sketch of the data, i.e. a low-dimensional vector of size $m \ll d^{2}$ carefully designed from $X$ using nonlinear random features. Under certain assumptions on the spectrum of $\Theta$ (or its condition number), we show that it is possible to estimate it from a sketch of size $m=\Omega((d+2k)\log(d))$ where $k$ is the maximal number of edges of the underlying graph. These information-theoretic guarantees are inspired by compressed sensing theory and involve restricted isometry properties and instance optimal decoders. We investigate the possibility of achieving practical recovery with an iterative algorithm based on the graphical lasso, viewed as a specific denoiser. We compare our approach and graphical lasso on synthetic datasets, demonstrating its favorable performance even when the dataset is compressed.

Implicit Differentiation for Hyperparameter Tuning the Weighted Graphical Lasso

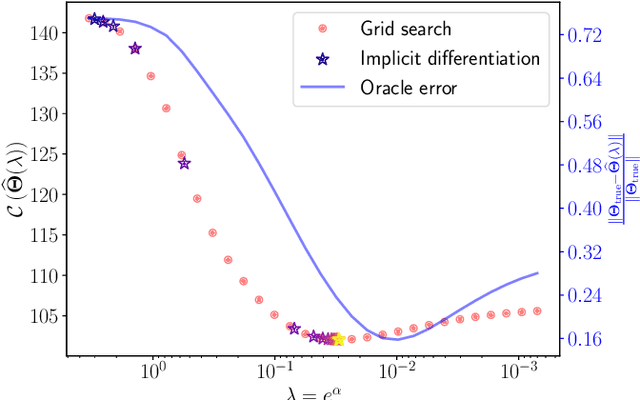
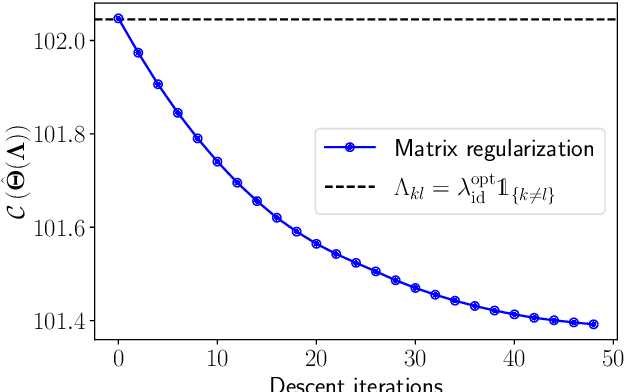
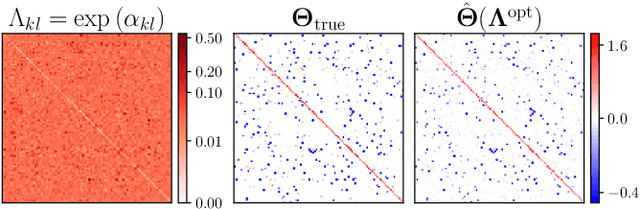
We provide a framework and algorithm for tuning the hyperparameters of the Graphical Lasso via a bilevel optimization problem solved with a first-order method. In particular, we derive the Jacobian of the Graphical Lasso solution with respect to its regularization hyperparameters.

Fast Multiscale Diffusion on Graphs

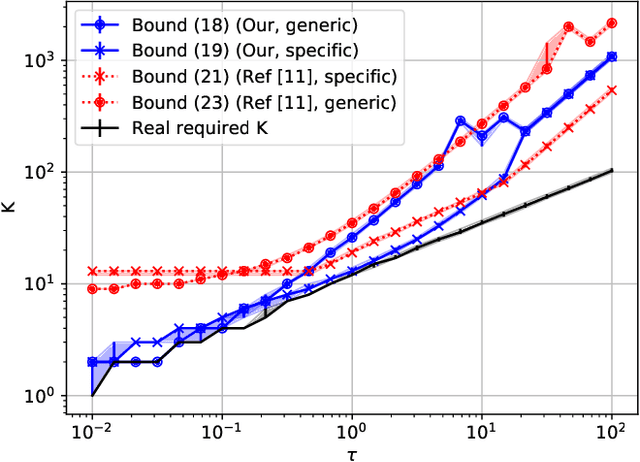
Diffusing a graph signal at multiple scales requires computing the action of the exponential of several multiples of the Laplacian matrix. We tighten a bound on the approximation error of truncated Chebyshev polynomial approximations of the exponential, hence significantly improving a priori estimates of the polynomial order for a prescribed error. We further exploit properties of these approximations to factorize the computation of the action of the diffusion operator over multiple scales, thus reducing drastically its computational cost.

Solving NMF with smoothness and sparsity constraints using PALM

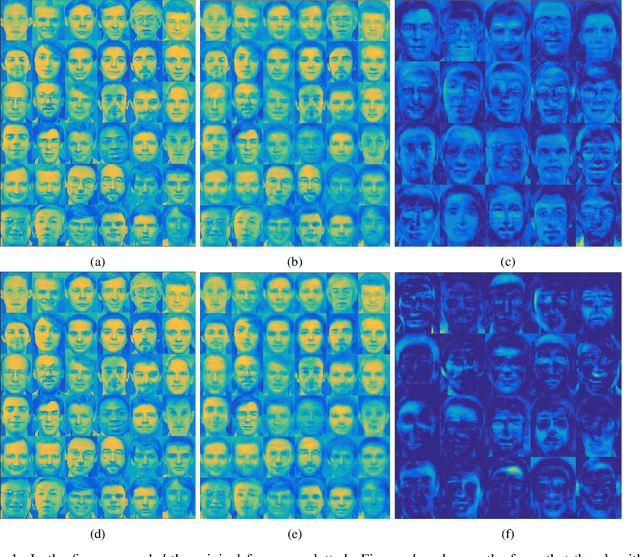
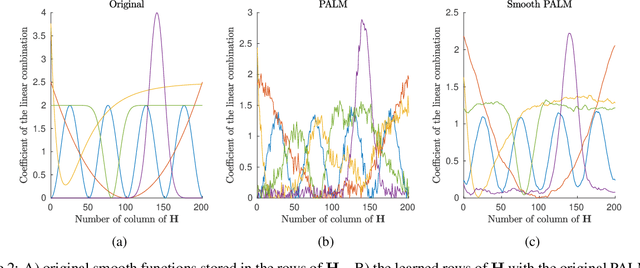
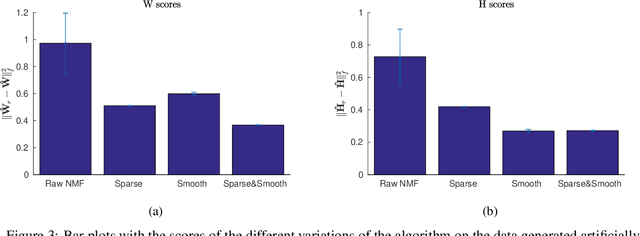
Non-negative matrix factorization is a problem of dimensionality reduction and source separation of data that has been widely used in many fields since it was studied in depth in 1999 by Lee and Seung, including in compression of data, document clustering, processing of audio spectrograms and astronomy. In this work we have adapted a minimization scheme for convex functions with non-differentiable constraints called PALM to solve the NMF problem with solutions that can be smooth and/or sparse, two properties frequently desired.

$L^γ$-PageRank for Semi-Supervised Learning

PageRank for Semi-Supervised Learning has shown to leverage data structures and limited tagged examples to yield meaningful classification. Despite successes, classification performance can still be improved, particularly in cases of fuzzy graphs or unbalanced labeled data. To address such limitations, a novel approach based on powers of the Laplacian matrix $L^\gamma$ ($\gamma > 0$), referred to as $L^\gamma$-PageRank, is proposed. Its theoretical study shows that it operates on signed graphs, where nodes belonging to one same class are more likely to share positive edges while nodes from different classes are more likely to be connected with negative edges. It is shown that by selecting an optimal $\gamma$, classification performance can be significantly enhanced. A procedure for the automated estimation of the optimal $\gamma$, from a unique observation of data, is devised and assessed. Experiments on several datasets demonstrate the effectiveness of both $L^\gamma$-PageRank classification and the optimal $\gamma$ estimation.