PASCO (PArallel Structured COarsening): an overlay to speed up graph clustering algorithms

Clustering the nodes of a graph is a cornerstone of graph analysis and has been extensively studied. However, some popular methods are not suitable for very large graphs: e.g., spectral clustering requires the computation of the spectral decomposition of the Laplacian matrix, which is not applicable for large graphs with a large number of communities. This work introduces PASCO, an overlay that accelerates clustering algorithms. Our method consists of three steps: 1-We compute several independent small graphs representing the input graph by applying an efficient and structure-preserving coarsening algorithm. 2-A clustering algorithm is run in parallel onto each small graph and provides several partitions of the initial graph. 3-These partitions are aligned and combined with an optimal transport method to output the final partition. The PASCO framework is based on two key contributions: a novel global algorithm structure designed to enable parallelization and a fast, empirically validated graph coarsening algorithm that preserves structural properties. We demonstrate the strong performance of 1 PASCO in terms of computational efficiency, structural preservation, and output partition quality, evaluated on both synthetic and real-world graph datasets.

Longitudinal Modularity, a Modularity for Link Streams

Temporal networks are commonly used to model real-life phenomena. When these phenomena represent interactions and are captured at a fine-grained temporal resolution, they are modeled as link streams. Community detection is an essential network analysis task. Although many methods exist for static networks, and some methods have been developed for temporal networks represented as sequences of snapshots, few works can handle link streams. This article introduces the first adaptation of the well-known Modularity quality function to link streams. Unlike existing methods, it is independent of the time scale of analysis. After introducing the quality function, and its relation to existing static and dynamic definitions of Modularity, we show experimentally its relevance for dynamic community evaluation.

A Comparative Analysis of Gene Expression Profiling by Statistical and Machine Learning Approaches

Many machine learning models have been proposed to classify phenotypes from gene expression data. In addition to their good performance, these models can potentially provide some understanding of phenotypes by extracting explanations for their decisions. These explanations often take the form of a list of genes ranked in order of importance for the predictions, the highest-ranked genes being interpreted as linked to the phenotype. We discuss the biological and the methodological limitations of such explanations. Experiments are performed on several datasets gathering cancer and healthy tissue samples from the TCGA, GTEx and TARGET databases. A collection of machine learning models including logistic regression, multilayer perceptron, and graph neural network are trained to classify samples according to their cancer type. Gene rankings are obtained from explainability methods adapted to these models, and compared to the ones from classical statistical feature selection methods such as mutual information, DESeq2, and EdgeR. Interestingly, on simple tasks, we observe that the information learned by black-box neural networks is related to the notion of differential expression. In all cases, a small set containing the best-ranked genes is sufficient to achieve a good classification. However, these genes differ significantly between the methods and similar classification performance can be achieved with numerous lower ranked genes. In conclusion, although these methods enable the identification of biomarkers characteristic of certain pathologies, our results question the completeness of the selected gene sets and thus of explainability by the identification of the underlying biological processes.

Studying Limits of Explainability by Integrated Gradients for Gene Expression Models

Understanding the molecular processes that drive cellular life is a fundamental question in biological research. Ambitious programs have gathered a number of molecular datasets on large populations. To decipher the complex cellular interactions, recent work has turned to supervised machine learning methods. The scientific questions are formulated as classical learning problems on tabular data or on graphs, e.g. phenotype prediction from gene expression data. In these works, the input features on which the individual predictions are predominantly based are often interpreted as indicative of the cause of the phenotype, such as cancer identification. Here, we propose to explore the relevance of the biomarkers identified by Integrated Gradients, an explainability method for feature attribution in machine learning. Through a motivating example on The Cancer Genome Atlas, we show that ranking features by importance is not enough to robustly identify biomarkers. As it is difficult to evaluate whether biomarkers reflect relevant causes without known ground truth, we simulate gene expression data by proposing a hierarchical model based on Latent Dirichlet Allocation models. We also highlight good practices for evaluating explanations for genomics data and propose a direction to derive more insights from these explanations.

Clustering with Simplicial Complexes

In this work, we propose a new clustering algorithm to group nodes in networks based on second-order simplices (aka filled triangles) to leverage higher-order network interactions. We define a simplicial conductance function, which on minimizing, yields an optimal partition with a higher density of filled triangles within the set while the density of filled triangles is smaller across the sets. To this end, we propose a simplicial adjacency operator that captures the relation between the nodes through second-order simplices. This allows us to extend the well-known Cheeger inequality to cluster a simplicial complex. Then, leveraging the Cheeger inequality, we propose the simplicial spectral clustering algorithm. We report results from numerical experiments on synthetic and real-world network data to demonstrate the efficacy of the proposed approach.

A simple way to learn metrics between attributed graphs

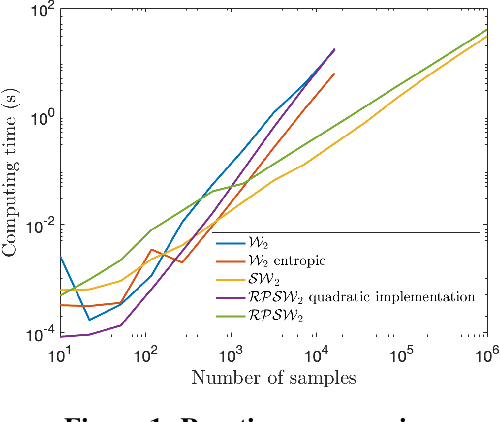
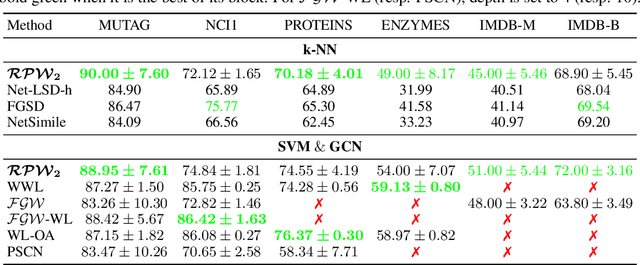
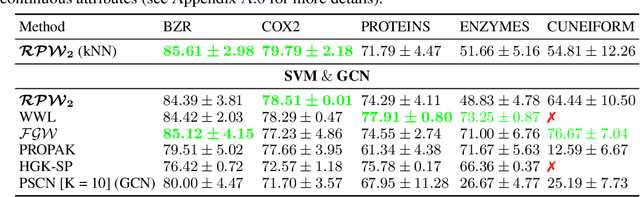
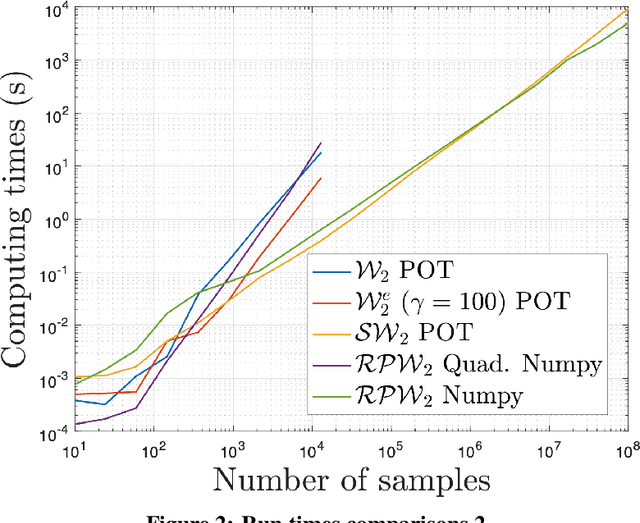
The choice of good distances and similarity measures between objects is important for many machine learning methods. Therefore, many metric learning algorithms have been developed in recent years, mainly for Euclidean data in order to improve performance of classification or clustering methods. However, due to difficulties in establishing computable, efficient and differentiable distances between attributed graphs, few metric learning algorithms adapted to graphs have been developed despite the strong interest of the community. In this paper, we address this issue by proposing a new Simple Graph Metric Learning - SGML - model with few trainable parameters based on Simple Graph Convolutional Neural Networks - SGCN - and elements of Optimal Transport theory. This model allows us to build an appropriate distance from a database of labeled (attributed) graphs to improve the performance of simple classification algorithms such as $k$-NN. This distance can be quickly trained while maintaining good performances as illustrated by the experimental study presented in this paper.

Probabilistic forecasts of extreme heatwaves using convolutional neural networks in a regime of lack of data

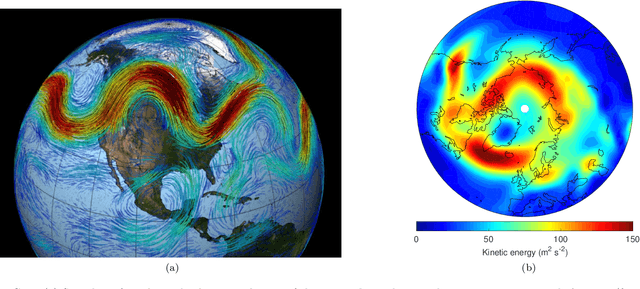
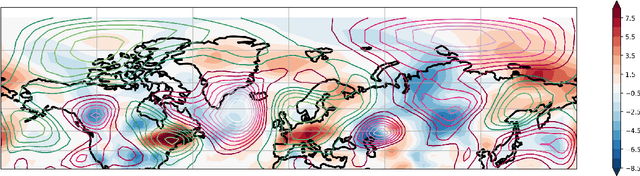
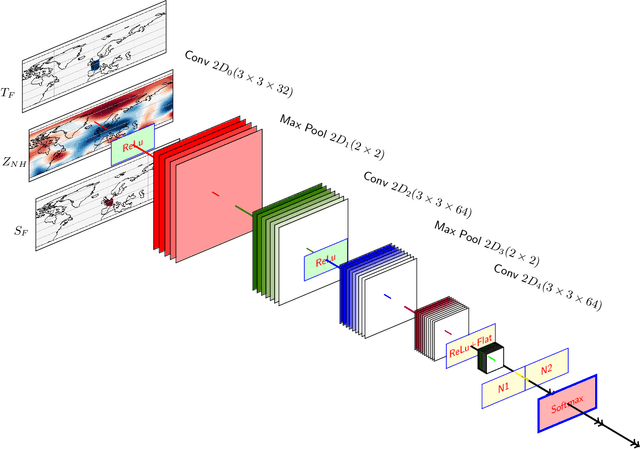
Understanding extreme events and their probability is key for the study of climate change impacts, risk assessment, adaptation, and the protection of living beings. In this work we develop a methodology to build forecasting models for extreme heatwaves. These models are based on convolutional neural networks, trained on extremely long 8,000-year climate model outputs. Because the relation between extreme events is intrinsically probabilistic, we emphasise probabilistic forecast and validation. We demonstrate that deep neural networks are suitable for this purpose for long lasting 14-day heatwaves over France, up to 15 days ahead of time for fast dynamical drivers (500 hPa geopotential height fields), and also at much longer lead times for slow physical drivers (soil moisture). The method is easily implemented and versatile. We find that the deep neural network selects extreme heatwaves associated with a North-Hemisphere wavenumber-3 pattern. We find that the 2 meter temperature field does not contain any new useful statistical information for heatwave forecast, when added to the 500 hPa geopotential height and soil moisture fields. The main scientific message is that training deep neural networks for predicting extreme heatwaves occurs in a regime of drastic lack of data. We suggest that this is likely the case for most other applications to large scale atmosphere and climate phenomena. We discuss perspectives for dealing with the lack of data regime, for instance rare event simulations, and how transfer learning may play a role in this latter task.

Fast Multiscale Diffusion on Graphs

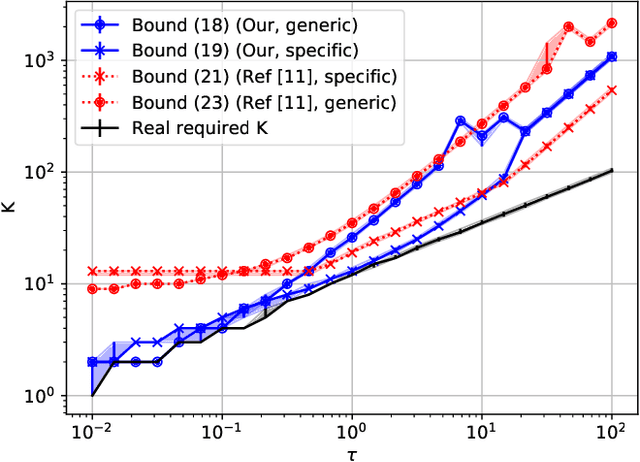
Diffusing a graph signal at multiple scales requires computing the action of the exponential of several multiples of the Laplacian matrix. We tighten a bound on the approximation error of truncated Chebyshev polynomial approximations of the exponential, hence significantly improving a priori estimates of the polynomial order for a prescribed error. We further exploit properties of these approximations to factorize the computation of the action of the diffusion operator over multiple scales, thus reducing drastically its computational cost.

Deep Learning based Extreme Heatwave Forecast

Forecasting the occurrence of heatwaves constitutes a challenging issue, yet of major societal stake, because extreme events are not often observed and (very) costly to simulate from physics-driven numerical models. The present work aims to explore the use of Deep Learning architectures as alternative strategies to predict extreme heatwaves occurrences from a very limited amount of available relevant climate data. This implies addressing issues such as the aggregation of climate data of different natures, the class-size imbalance that is intrinsically associated with rare event prediction, and the potential benefits of transfer learning to address the nested nature of extreme events (naturally included in less extreme ones). Using 1000 years of state-of-the-art PlaSim Planete Simulator Climate Model data, it is shown that Convolutional Neural Network-based Deep Learning frameworks, with large-class undersampling and transfer learning achieve significant performance in forecasting the occurrence of extreme heatwaves, at three different levels of intensity, and as early as 15 days in advance from the restricted observation, for a single time (single snapshoot) of only two spatial fields of climate data, surface temperature and geopotential height.

Multiview Variational Graph Autoencoders for Canonical Correlation Analysis

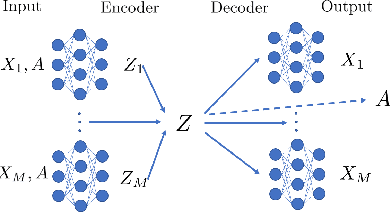
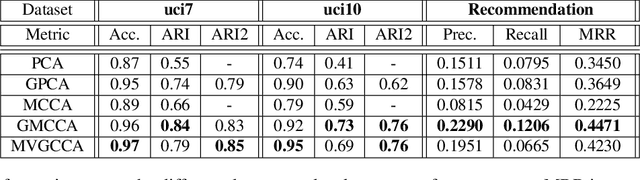
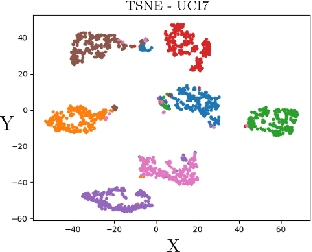
We present a novel multiview canonical correlation analysis model based on a variational approach. This is the first nonlinear model that takes into account the available graph-based geometric constraints while being scalable for processing large scale datasets with multiple views. It is based on an autoencoder architecture with graph convolutional neural network layers. We experiment with our approach on classification, clustering, and recommendation tasks on real datasets. The algorithm is competitive with state-of-the-art multiview representation learning techniques.