Amaury Habrard
LHC
From GNNs to Symbolic Surrogates via Kolmogorov-Arnold Networks for Delay Prediction
Dec 24, 2025Abstract:Accurate prediction of flow delay is essential for optimizing and managing modern communication networks. We investigate three levels of modeling for this task. First, we implement a heterogeneous GNN with attention-based message passing, establishing a strong neural baseline. Second, we propose FlowKANet in which Kolmogorov-Arnold Networks replace standard MLP layers, reducing trainable parameters while maintaining competitive predictive performance. FlowKANet integrates KAMP-Attn (Kolmogorov-Arnold Message Passing with Attention), embedding KAN operators directly into message-passing and attention computation. Finally, we distill the model into symbolic surrogate models using block-wise regression, producing closed-form equations that eliminate trainable weights while preserving graph-structured dependencies. The results show that KAN layers provide a favorable trade-off between efficiency and accuracy and that symbolic surrogates emphasize the potential for lightweight deployment and enhanced transparency.
Interpretable Reinforcement Learning for Load Balancing using Kolmogorov-Arnold Networks
May 20, 2025Abstract:Reinforcement learning (RL) has been increasingly applied to network control problems, such as load balancing. However, existing RL approaches often suffer from lack of interpretability and difficulty in extracting controller equations. In this paper, we propose the use of Kolmogorov-Arnold Networks (KAN) for interpretable RL in network control. We employ a PPO agent with a 1-layer actor KAN model and an MLP Critic network to learn load balancing policies that maximise throughput utility, minimize loss as well as delay. Our approach allows us to extract controller equations from the learned neural networks, providing insights into the decision-making process. We evaluate our approach using different reward functions demonstrating its effectiveness in improving network performance while providing interpretable policies.
Provably accurate adaptive sampling for collocation points in physics-informed neural networks
Apr 01, 2025Abstract:Despite considerable scientific advances in numerical simulation, efficiently solving PDEs remains a complex and often expensive problem. Physics-informed Neural Networks (PINN) have emerged as an efficient way to learn surrogate solvers by embedding the PDE in the loss function and minimizing its residuals using automatic differentiation at so-called collocation points. Originally uniformly sampled, the choice of the latter has been the subject of recent advances leading to adaptive sampling refinements for PINNs. In this paper, leveraging a new quadrature method for approximating definite integrals, we introduce a provably accurate sampling method for collocation points based on the Hessian of the PDE residuals. Comparative experiments conducted on a set of 1D and 2D PDEs demonstrate the benefits of our method.
Leveraging PAC-Bayes Theory and Gibbs Distributions for Generalization Bounds with Complexity Measures
Feb 19, 2024
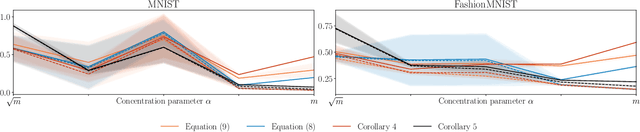
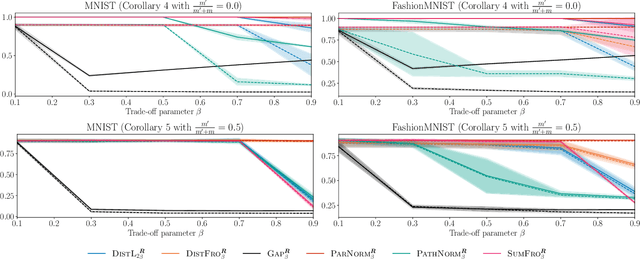
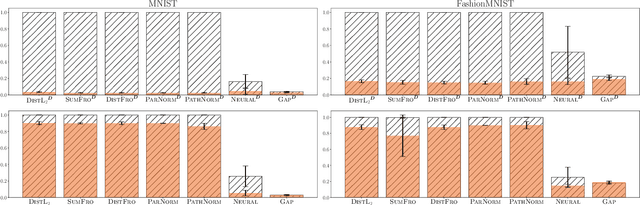
Abstract:In statistical learning theory, a generalization bound usually involves a complexity measure imposed by the considered theoretical framework. This limits the scope of such bounds, as other forms of capacity measures or regularizations are used in algorithms. In this paper, we leverage the framework of disintegrated PAC-Bayes bounds to derive a general generalization bound instantiable with arbitrary complexity measures. One trick to prove such a result involves considering a commonly used family of distributions: the Gibbs distributions. Our bound stands in probability jointly over the hypothesis and the learning sample, which allows the complexity to be adapted to the generalization gap as it can be customized to fit both the hypothesis class and the task.
Towards Few-Annotation Learning for Object Detection: Are Transformer-based Models More Efficient ?
Oct 30, 2023Abstract:For specialized and dense downstream tasks such as object detection, labeling data requires expertise and can be very expensive, making few-shot and semi-supervised models much more attractive alternatives. While in the few-shot setup we observe that transformer-based object detectors perform better than convolution-based two-stage models for a similar amount of parameters, they are not as effective when used with recent approaches in the semi-supervised setting. In this paper, we propose a semi-supervised method tailored for the current state-of-the-art object detector Deformable DETR in the few-annotation learning setup using a student-teacher architecture, which avoids relying on a sensitive post-processing of the pseudo-labels generated by the teacher model. We evaluate our method on the semi-supervised object detection benchmarks COCO and Pascal VOC, and it outperforms previous methods, especially when annotations are scarce. We believe that our contributions open new possibilities to adapt similar object detection methods in this setup as well.
Proposal-Contrastive Pretraining for Object Detection from Fewer Data
Oct 25, 2023Abstract:The use of pretrained deep neural networks represents an attractive way to achieve strong results with few data available. When specialized in dense problems such as object detection, learning local rather than global information in images has proven to be more efficient. However, for unsupervised pretraining, the popular contrastive learning requires a large batch size and, therefore, a lot of resources. To address this problem, we are interested in transformer-based object detectors that have recently gained traction in the community with good performance and with the particularity of generating many diverse object proposals. In this work, we present Proposal Selection Contrast (ProSeCo), a novel unsupervised overall pretraining approach that leverages this property. ProSeCo uses the large number of object proposals generated by the detector for contrastive learning, which allows the use of a smaller batch size, combined with object-level features to learn local information in the images. To improve the effectiveness of the contrastive loss, we introduce the object location information in the selection of positive examples to take into account multiple overlapping object proposals. When reusing pretrained backbone, we advocate for consistency in learning local information between the backbone and the detection head. We show that our method outperforms state of the art in unsupervised pretraining for object detection on standard and novel benchmarks in learning with fewer data.
A simple way to learn metrics between attributed graphs
Sep 26, 2022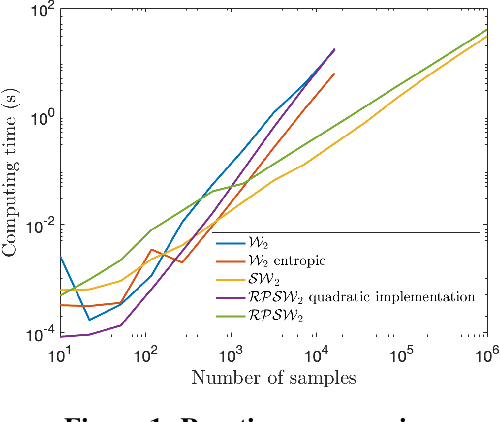
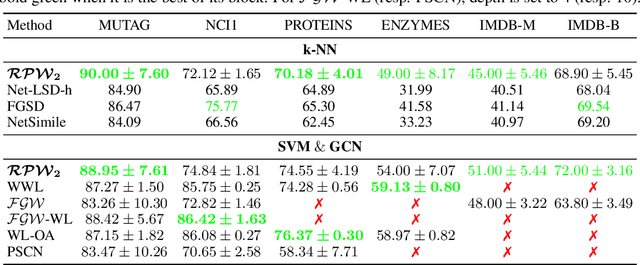
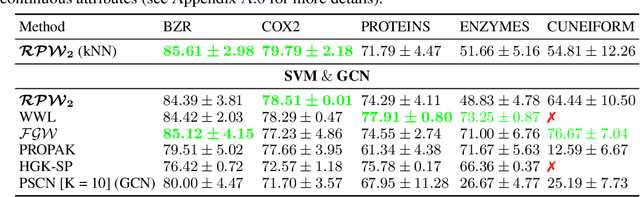
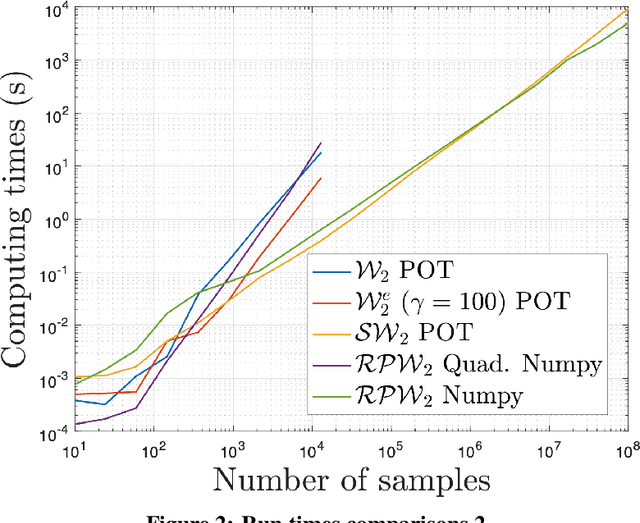
Abstract:The choice of good distances and similarity measures between objects is important for many machine learning methods. Therefore, many metric learning algorithms have been developed in recent years, mainly for Euclidean data in order to improve performance of classification or clustering methods. However, due to difficulties in establishing computable, efficient and differentiable distances between attributed graphs, few metric learning algorithms adapted to graphs have been developed despite the strong interest of the community. In this paper, we address this issue by proposing a new Simple Graph Metric Learning - SGML - model with few trainable parameters based on Simple Graph Convolutional Neural Networks - SGCN - and elements of Optimal Transport theory. This model allows us to build an appropriate distance from a database of labeled (attributed) graphs to improve the performance of simple classification algorithms such as $k$-NN. This distance can be quickly trained while maintaining good performances as illustrated by the experimental study presented in this paper.
Learning Stochastic Majority Votes by Minimizing a PAC-Bayes Generalization Bound
Jun 23, 2021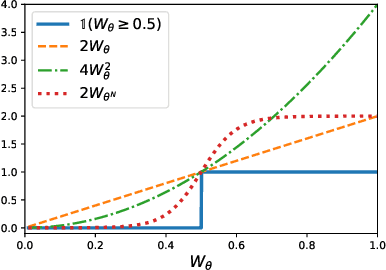
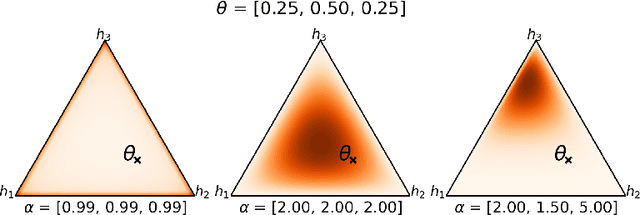
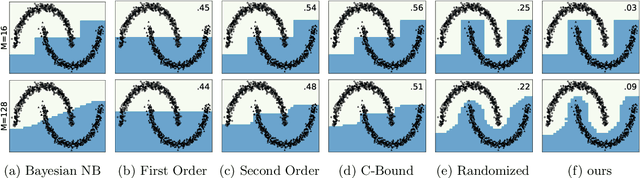
Abstract:We investigate a stochastic counterpart of majority votes over finite ensembles of classifiers, and study its generalization properties. While our approach holds for arbitrary distributions, we instantiate it with Dirichlet distributions: this allows for a closed-form and differentiable expression for the expected risk, which then turns the generalization bound into a tractable training objective. The resulting stochastic majority vote learning algorithm achieves state-of-the-art accuracy and benefits from (non-vacuous) tight generalization bounds, in a series of numerical experiments when compared to competing algorithms which also minimize PAC-Bayes objectives -- both with uninformed (data-independent) and informed (data-dependent) priors.
Self-Bounding Majority Vote Learning Algorithms by the Direct Minimization of a Tight PAC-Bayesian C-Bound
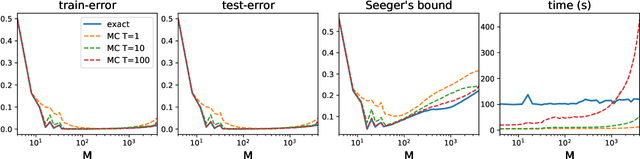
Apr 28, 2021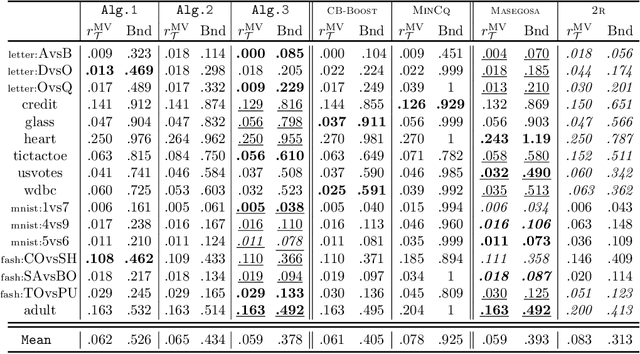
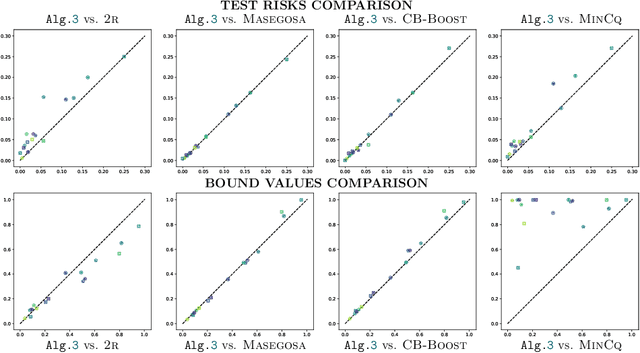

Abstract:In the PAC-Bayesian literature, the C-Bound refers to an insightful relation between the risk of a majority vote classifier (under the zero-one loss) and the first two moments of its margin (i.e., the expected margin and the voters' diversity). Until now, learning algorithms developed in this framework minimize the empirical version of the C-Bound, instead of explicit PAC-Bayesian generalization bounds. In this paper, by directly optimizing PAC-Bayesian guarantees on the C-Bound, we derive self-bounding majority vote learning algorithms. Moreover, our algorithms based on gradient descent are scalable and lead to accurate predictors paired with non-vacuous guarantees.
A PAC-Bayes Analysis of Adversarial Robustness
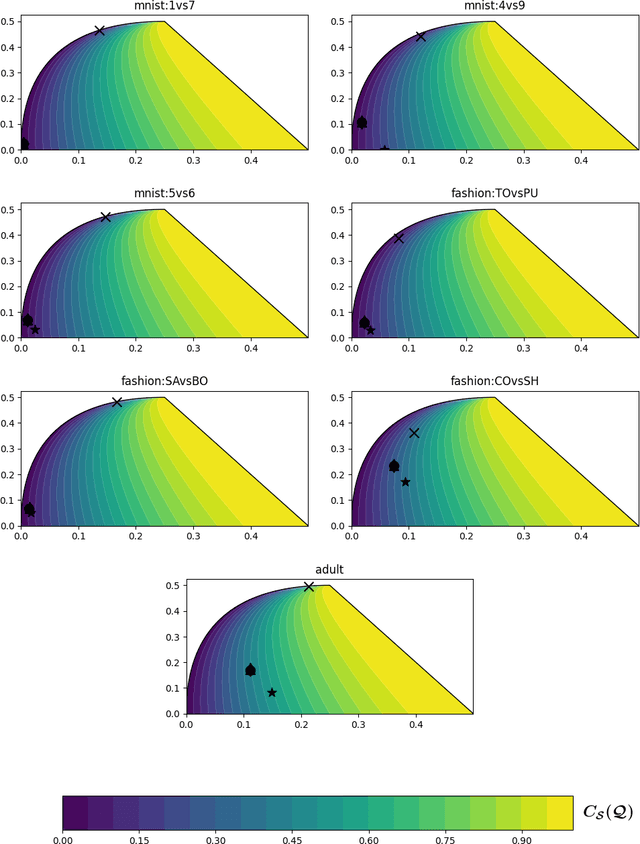
Feb 19, 2021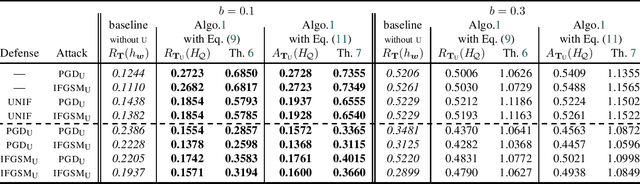
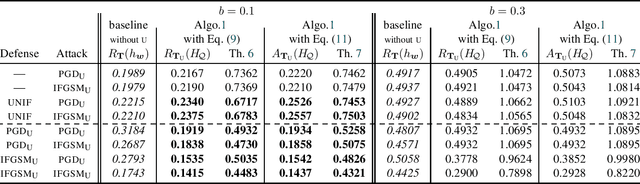
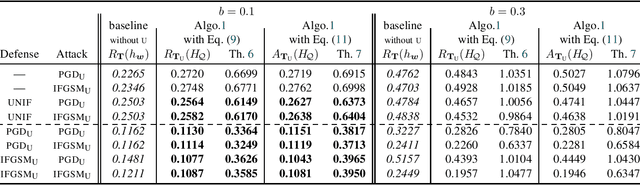
Abstract:We propose the first general PAC-Bayesian generalization bounds for adversarial robustness, that estimate, at test time, how much a model will be invariant to imperceptible perturbations in the input. Instead of deriving a worst-case analysis of the risk of a hypothesis over all the possible perturbations, we leverage the PAC-Bayesian framework to bound the averaged risk on the perturbations for majority votes (over the whole class of hypotheses). Our theoretically founded analysis has the advantage to provide general bounds (i) independent from the type of perturbations (i.e., the adversarial attacks), (ii) that are tight thanks to the PAC-Bayesian framework, (iii) that can be directly minimized during the learning phase to obtain a robust model on different attacks at test time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge