Fast Multiscale Diffusion on Graphs

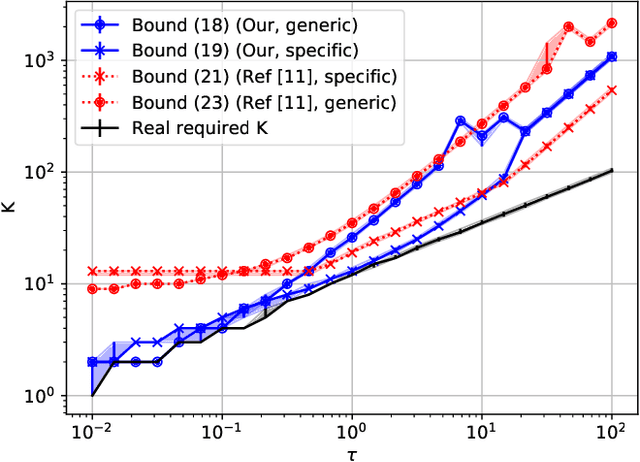
Diffusing a graph signal at multiple scales requires computing the action of the exponential of several multiples of the Laplacian matrix. We tighten a bound on the approximation error of truncated Chebyshev polynomial approximations of the exponential, hence significantly improving a priori estimates of the polynomial order for a prescribed error. We further exploit properties of these approximations to factorize the computation of the action of the diffusion operator over multiple scales, thus reducing drastically its computational cost.

A survey on domain adaptation theory

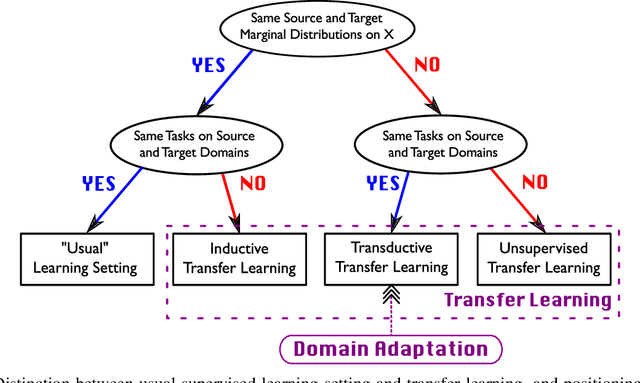
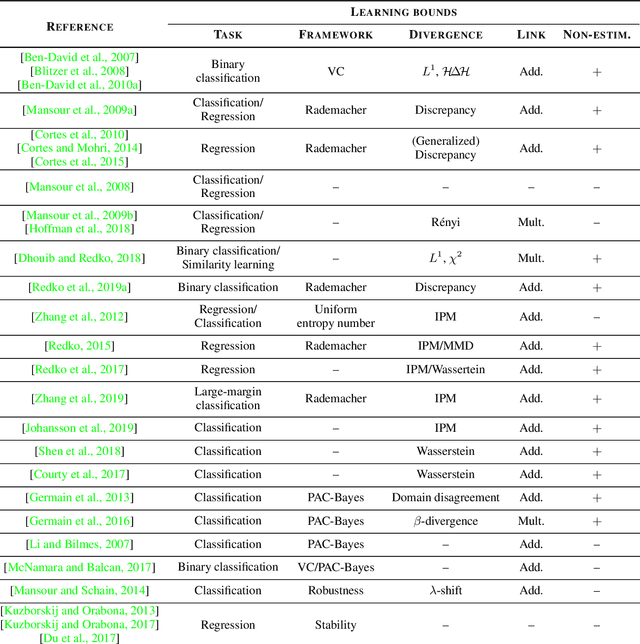
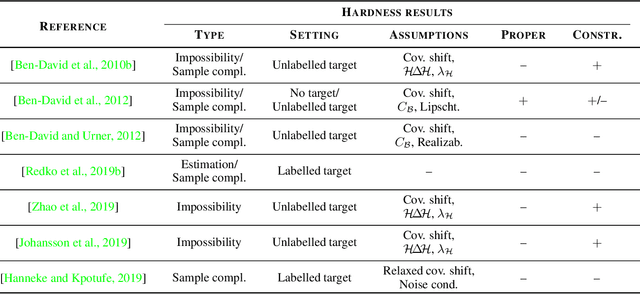
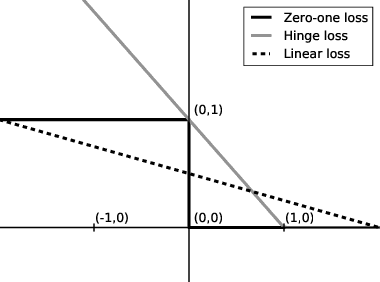
All famous machine learning algorithms that correspond to both supervised and semi-supervised learning work well only under a common assumption: training and test data follow the same distribution. When the distribution changes, most statistical models must be reconstructed from new collected data that, for some applications, may be costly or impossible to get. Therefore, it became necessary to develop approaches that reduce the need and the effort of obtaining new labeled samples by exploiting data available in related areas and using it further in similar fields. This has given rise to a new machine learning framework called transfer learning: a learning setting inspired by the capability of a human being to extrapolate knowledge across tasks to learn more efficiently. Despite a large amount of different transfer learning scenarios, the main objective of this survey is to provide an overview of the state-of-the-art theoretical results in a specific and arguably the most popular sub-field of transfer learning called domain adaptation. In this sub-field, the data distribution is assumed to change across the training and the test data while the learning task remains the same. We provide a first up-to-date description of existing results related to domain adaptation problem that cover learning bounds based on different statistical learning frameworks.

Metric Learning from Imbalanced Data

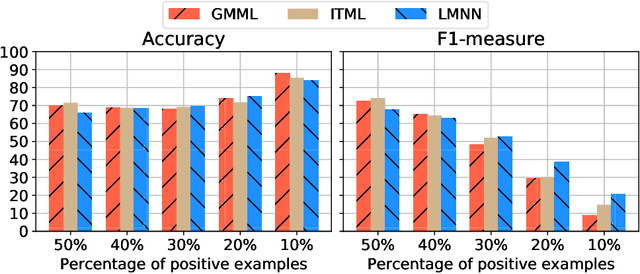
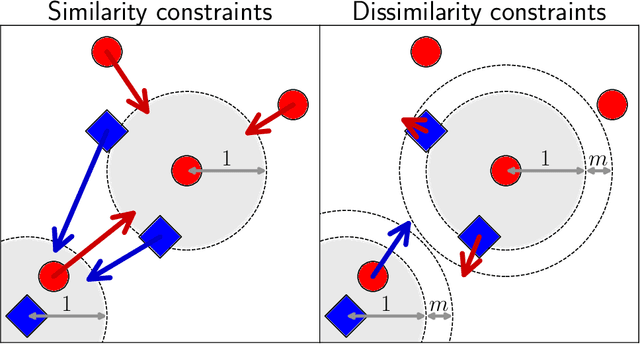
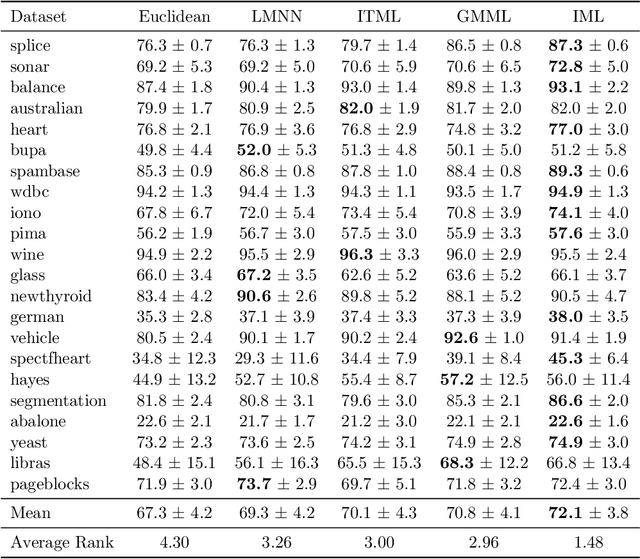
A key element of any machine learning algorithm is the use of a function that measures the dis/similarity between data points. Given a task, such a function can be optimized with a metric learning algorithm. Although this research field has received a lot of attention during the past decade, very few approaches have focused on learning a metric in an imbalanced scenario where the number of positive examples is much smaller than the negatives. Here, we address this challenging task by designing a new Mahalanobis metric learning algorithm (IML) which deals with class imbalance. The empirical study performed shows the efficiency of IML.

An Adjusted Nearest Neighbor Algorithm Maximizing the F-Measure from Imbalanced Data

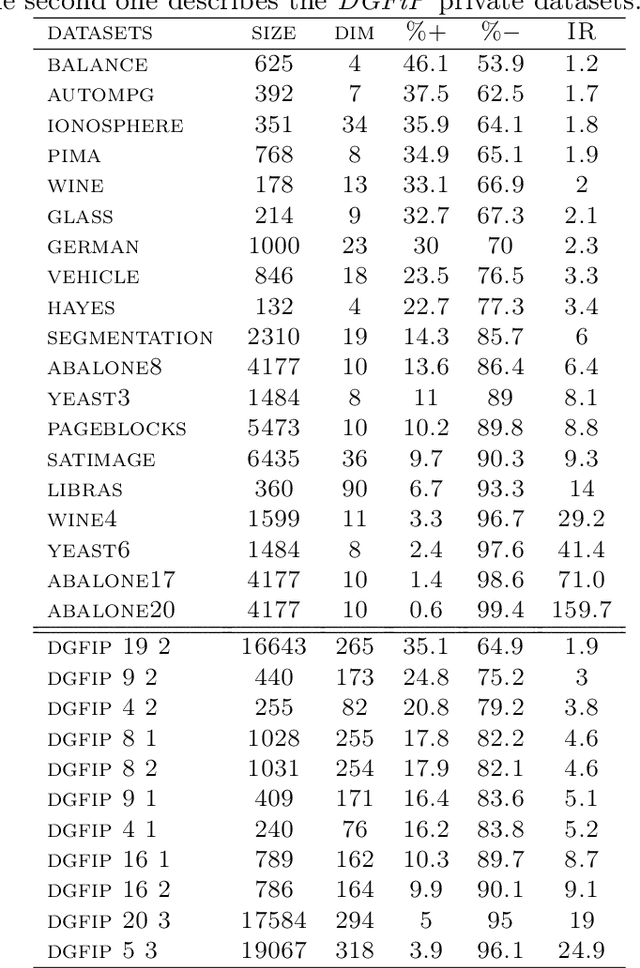
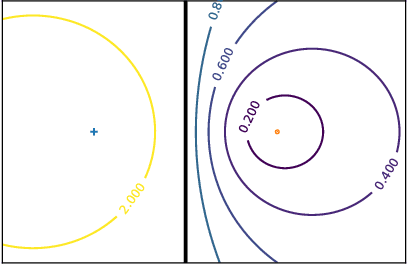
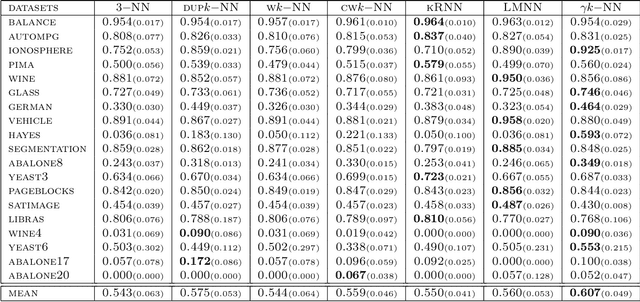
In this paper, we address the challenging problem of learning from imbalanced data using a Nearest-Neighbor (NN) algorithm. In this setting, the minority examples typically belong to the class of interest requiring the optimization of specific criteria, like the F-Measure. Based on simple geometrical ideas, we introduce an algorithm that reweights the distance between a query sample and any positive training example. This leads to a modification of the Voronoi regions and thus of the decision boundaries of the NN algorithm. We provide a theoretical justification about the weighting scheme needed to reduce the False Negative rate while controlling the number of False Positives. We perform an extensive experimental study on many public imbalanced datasets, but also on large scale non public data from the French Ministry of Economy and Finance on a tax fraud detection task, showing that our method is very effective and, interestingly, yields the best performance when combined with state of the art sampling methods.

Learning Landmark-Based Ensembles with Random Fourier Features and Gradient Boosting

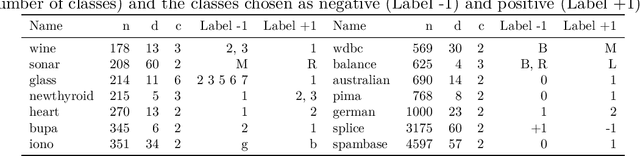
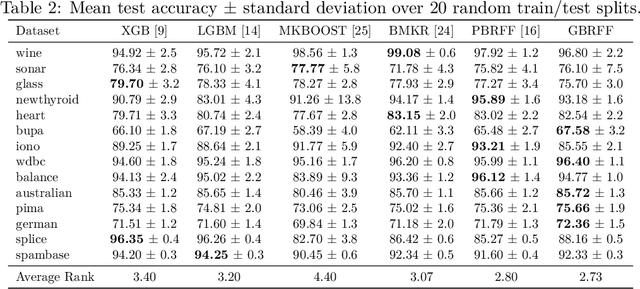
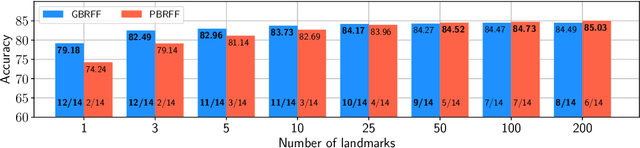
We propose a Gradient Boosting algorithm for learning an ensemble of kernel functions adapted to the task at hand. Unlike state-of-the-art Multiple Kernel Learning techniques that make use of a pre-computed dictionary of kernel functions to select from, at each iteration we fit a kernel by approximating it as a weighted sum of Random Fourier Features (RFF) and by optimizing their barycenter. This allows us to obtain a more versatile method, easier to setup and likely to have better performance. Our study builds on a recent result showing one can learn a kernel from RFF by computing the minimum of a PAC-Bayesian bound on the kernel alignment generalization loss, which is obtained efficiently from a closed-form solution. We conduct an experimental analysis to highlight the advantages of our method w.r.t. both Boosting-based and kernel-learning state-of-the-art methods.

Theoretical Analysis of Domain Adaptation with Optimal Transport

Domain adaptation (DA) is an important and emerging field of machine learning that tackles the problem occurring when the distributions of training (source domain) and test (target domain) data are similar but different. Current theoretical results show that the efficiency of DA algorithms depends on their capacity of minimizing the divergence between source and target probability distributions. In this paper, we provide a theoretical study on the advantages that concepts borrowed from optimal transportation theory can bring to DA. In particular, we show that the Wasserstein metric can be used as a divergence measure between distributions to obtain generalization guarantees for three different learning settings: (i) classic DA with unsupervised target data (ii) DA combining source and target labeled data, (iii) multiple source DA. Based on the obtained results, we provide some insights showing when this analysis can be tighter than other existing frameworks.

L$^3$-SVMs: Landmarks-based Linear Local Support Vectors Machines

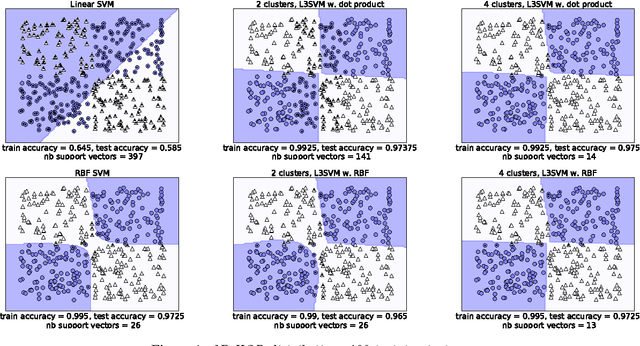
For their ability to capture non-linearities in the data and to scale to large training sets, local Support Vector Machines (SVMs) have received a special attention during the past decade. In this paper, we introduce a new local SVM method, called L$^3$-SVMs, which clusters the input space, carries out dimensionality reduction by projecting the data on landmarks, and jointly learns a linear combination of local models. Simple and effective, our algorithm is also theoretically well-founded. Using the framework of Uniform Stability, we show that our SVM formulation comes with generalization guarantees on the true risk. The experiments based on the simplest configuration of our model (i.e. landmarks randomly selected, linear projection, linear kernel) show that L$^3$-SVMs is very competitive w.r.t. the state of the art and opens the door to new exciting lines of research.

Similarity Learning for Time Series Classification

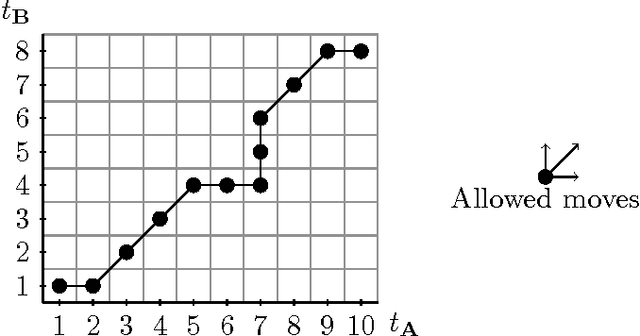
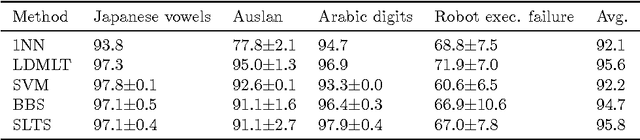
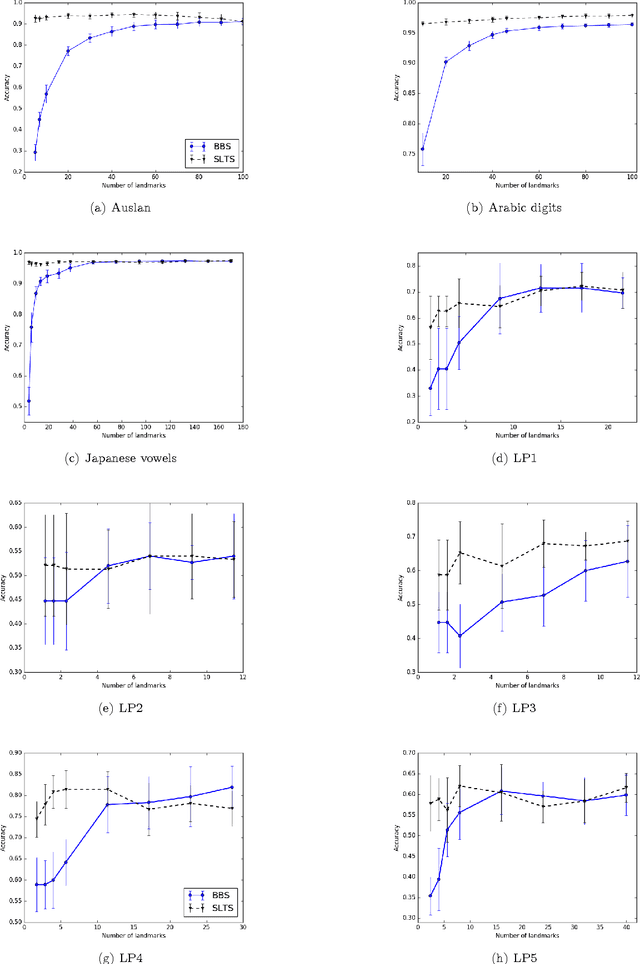
Multivariate time series naturally exist in many fields, like energy, bioinformatics, signal processing, and finance. Most of these applications need to be able to compare these structured data. In this context, dynamic time warping (DTW) is probably the most common comparison measure. However, not much research effort has been put into improving it by learning. In this paper, we propose a novel method for learning similarities based on DTW, in order to improve time series classification. Making use of the uniform stability framework, we provide the first theoretical guarantees in the form of a generalization bound for linear classification. The experimental study shows that the proposed approach is efficient, while yielding sparse classifiers.

Lipschitz Continuity of Mahalanobis Distances and Bilinear Forms

Many theoretical results in the machine learning domain stand only for functions that are Lipschitz continuous. Lipschitz continuity is a strong form of continuity that linearly bounds the variations of a function. In this paper, we derive tight Lipschitz constants for two families of metrics: Mahalanobis distances and bounded-space bilinear forms. To our knowledge, this is the first time the Mahalanobis distance is formally proved to be Lipschitz continuous and that such tight Lipschitz constants are derived.

Algorithmic Robustness for Learning via $(ε, γ, τ)$-Good Similarity Functions

The notion of metric plays a key role in machine learning problems such as classification, clustering or ranking. However, it is worth noting that there is a severe lack of theoretical guarantees that can be expected on the generalization capacity of the classifier associated to a given metric. The theoretical framework of $(\epsilon, \gamma, \tau)$-good similarity functions (Balcan et al., 2008) has been one of the first attempts to draw a link between the properties of a similarity function and those of a linear classifier making use of it. In this paper, we extend and complete this theory by providing a new generalization bound for the associated classifier based on the algorithmic robustness framework.