L$^3$-SVMs: Landmarks-based Linear Local Support Vectors Machines
Paper and Code
Apr 03, 2017
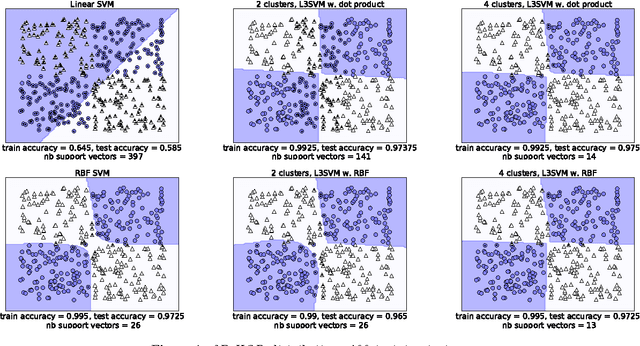


For their ability to capture non-linearities in the data and to scale to large training sets, local Support Vector Machines (SVMs) have received a special attention during the past decade. In this paper, we introduce a new local SVM method, called L$^3$-SVMs, which clusters the input space, carries out dimensionality reduction by projecting the data on landmarks, and jointly learns a linear combination of local models. Simple and effective, our algorithm is also theoretically well-founded. Using the framework of Uniform Stability, we show that our SVM formulation comes with generalization guarantees on the true risk. The experiments based on the simplest configuration of our model (i.e. landmarks randomly selected, linear projection, linear kernel) show that L$^3$-SVMs is very competitive w.r.t. the state of the art and opens the door to new exciting lines of research.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge