Bridging Arbitrary and Tree Metrics via Differentiable Gromov Hyperbolicity

Trees and the associated shortest-path tree metrics provide a powerful framework for representing hierarchical and combinatorial structures in data. Given an arbitrary metric space, its deviation from a tree metric can be quantified by Gromov's $\delta$-hyperbolicity. Nonetheless, designing algorithms that bridge an arbitrary metric to its closest tree metric is still a vivid subject of interest, as most common approaches are either heuristical and lack guarantees, or perform moderately well. In this work, we introduce a novel differentiable optimization framework, coined DeltaZero, that solves this problem. Our method leverages a smooth surrogate for Gromov's $\delta$-hyperbolicity which enables a gradient-based optimization, with a tractable complexity. The corresponding optimization procedure is derived from a problem with better worst case guarantees than existing bounds, and is justified statistically. Experiments on synthetic and real-world datasets demonstrate that our method consistently achieves state-of-the-art distortion.

A note on the relations between mixture models, maximum-likelihood and entropic optimal transport

This note aims to demonstrate that performing maximum-likelihood estimation for a mixture model is equivalent to minimizing over the parameters an optimal transport problem with entropic regularization. The objective is pedagogical: we seek to present this already known result in a concise and hopefully simple manner. We give an illustration with Gaussian mixture models by showing that the standard EM algorithm is a specific block-coordinate descent on an optimal transport loss.

PASCO (PArallel Structured COarsening): an overlay to speed up graph clustering algorithms

Clustering the nodes of a graph is a cornerstone of graph analysis and has been extensively studied. However, some popular methods are not suitable for very large graphs: e.g., spectral clustering requires the computation of the spectral decomposition of the Laplacian matrix, which is not applicable for large graphs with a large number of communities. This work introduces PASCO, an overlay that accelerates clustering algorithms. Our method consists of three steps: 1-We compute several independent small graphs representing the input graph by applying an efficient and structure-preserving coarsening algorithm. 2-A clustering algorithm is run in parallel onto each small graph and provides several partitions of the initial graph. 3-These partitions are aligned and combined with an optimal transport method to output the final partition. The PASCO framework is based on two key contributions: a novel global algorithm structure designed to enable parallelization and a fast, empirically validated graph coarsening algorithm that preserves structural properties. We demonstrate the strong performance of 1 PASCO in terms of computational efficiency, structural preservation, and output partition quality, evaluated on both synthetic and real-world graph datasets.

Schur's Positive-Definite Network: Deep Learning in the SPD cone with structure

Estimating matrices in the symmetric positive-definite (SPD) cone is of interest for many applications ranging from computer vision to graph learning. While there exist various convex optimization-based estimators, they remain limited in expressivity due to their model-based approach. The success of deep learning has thus led many to use neural networks to learn to estimate SPD matrices in a data-driven fashion. For learning structured outputs, one promising strategy involves architectures designed by unrolling iterative algorithms, which potentially benefit from inductive bias properties. However, designing correct unrolled architectures for SPD learning is difficult: they either do not guarantee that their output has all the desired properties, rely on heavy computations, or are overly restrained to specific matrices which hinders their expressivity. In this paper, we propose a novel and generic learning module with guaranteed SPD outputs called SpodNet, that also enables learning a larger class of functions than existing approaches. Notably, it solves the challenging task of learning jointly SPD and sparse matrices. Our experiments demonstrate the versatility of SpodNet layers.

Distributional Reduction: Unifying Dimensionality Reduction and Clustering with Gromov-Wasserstein Projection

Unsupervised learning aims to capture the underlying structure of potentially large and high-dimensional datasets. Traditionally, this involves using dimensionality reduction methods to project data onto interpretable spaces or organizing points into meaningful clusters. In practice, these methods are used sequentially, without guaranteeing that the clustering aligns well with the conducted dimensionality reduction. In this work, we offer a fresh perspective: that of distributions. Leveraging tools from optimal transport, particularly the Gromov-Wasserstein distance, we unify clustering and dimensionality reduction into a single framework called distributional reduction. This allows us to jointly address clustering and dimensionality reduction with a single optimization problem. Through comprehensive experiments, we highlight the versatility and interpretability of our method and show that it outperforms existing approaches across a variety of image and genomics datasets.

Compressive Recovery of Sparse Precision Matrices

We consider the problem of learning a graph modeling the statistical relations of the $d$ variables of a dataset with $n$ samples $X \in \mathbb{R}^{n \times d}$. Standard approaches amount to searching for a precision matrix $\Theta$ representative of a Gaussian graphical model that adequately explains the data. However, most maximum likelihood-based estimators usually require storing the $d^{2}$ values of the empirical covariance matrix, which can become prohibitive in a high-dimensional setting. In this work, we adopt a compressive viewpoint and aim to estimate a sparse $\Theta$ from a sketch of the data, i.e. a low-dimensional vector of size $m \ll d^{2}$ carefully designed from $X$ using nonlinear random features. Under certain assumptions on the spectrum of $\Theta$ (or its condition number), we show that it is possible to estimate it from a sketch of size $m=\Omega((d+2k)\log(d))$ where $k$ is the maximal number of edges of the underlying graph. These information-theoretic guarantees are inspired by compressed sensing theory and involve restricted isometry properties and instance optimal decoders. We investigate the possibility of achieving practical recovery with an iterative algorithm based on the graphical lasso, viewed as a specific denoiser. We compare our approach and graphical lasso on synthetic datasets, demonstrating its favorable performance even when the dataset is compressed.

Interpolating between Clustering and Dimensionality Reduction with Gromov-Wasserstein

We present a versatile adaptation of existing dimensionality reduction (DR) objectives, enabling the simultaneous reduction of both sample and feature sizes. Correspondances between input and embedding samples are computed through a semi-relaxed Gromov-Wasserstein optimal transport (OT) problem. When the embedding sample size matches that of the input, our model recovers classical popular DR models. When the embedding's dimensionality is unconstrained, we show that the OT plan delivers a competitive hard clustering. We emphasize the importance of intermediate stages that blend DR and clustering for summarizing real data and apply our method to visualize datasets of images.

Optimal Transport with Adaptive Regularisation

Regularising the primal formulation of optimal transport (OT) with a strictly convex term leads to enhanced numerical complexity and a denser transport plan. Many formulations impose a global constraint on the transport plan, for instance by relying on entropic regularisation. As it is more expensive to diffuse mass for outlier points compared to central ones, this typically results in a significant imbalance in the way mass is spread across the points. This can be detrimental for some applications where a minimum of smoothing is required per point. To remedy this, we introduce OT with Adaptive RegularIsation (OTARI), a new formulation of OT that imposes constraints on the mass going in or/and out of each point. We then showcase the benefits of this approach for domain adaptation.

Implicit Differentiation for Hyperparameter Tuning the Weighted Graphical Lasso

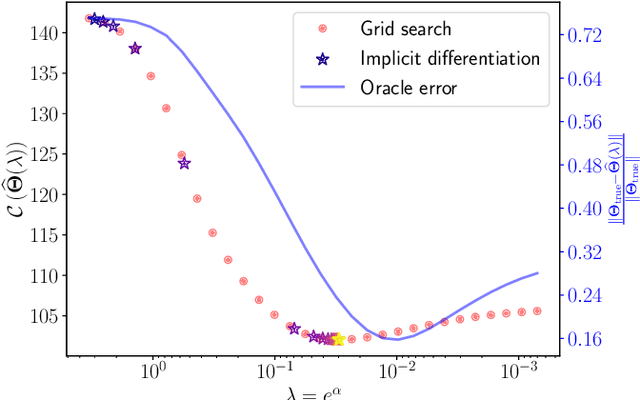
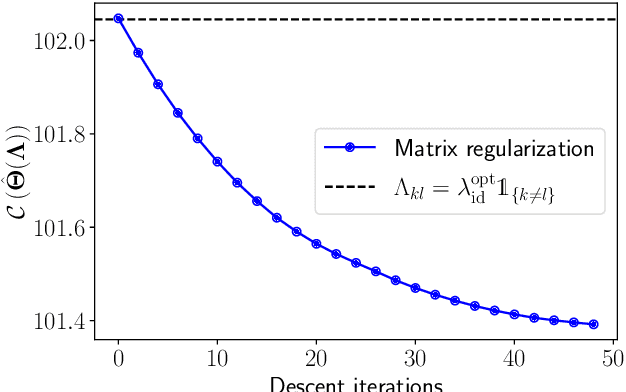
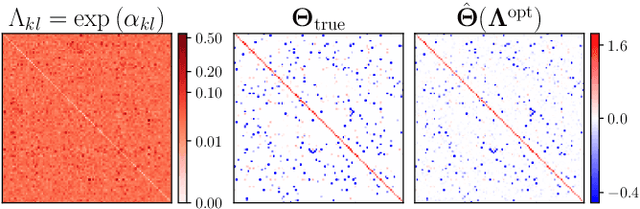
We provide a framework and algorithm for tuning the hyperparameters of the Graphical Lasso via a bilevel optimization problem solved with a first-order method. In particular, we derive the Jacobian of the Graphical Lasso solution with respect to its regularization hyperparameters.

SNEkhorn: Dimension Reduction with Symmetric Entropic Affinities

Many approaches in machine learning rely on a weighted graph to encode the similarities between samples in a dataset. Entropic affinities (EAs), which are notably used in the popular Dimensionality Reduction (DR) algorithm t-SNE, are particular instances of such graphs. To ensure robustness to heterogeneous sampling densities, EAs assign a kernel bandwidth parameter to every sample in such a way that the entropy of each row in the affinity matrix is kept constant at a specific value, whose exponential is known as perplexity. EAs are inherently asymmetric and row-wise stochastic, but they are used in DR approaches after undergoing heuristic symmetrization methods that violate both the row-wise constant entropy and stochasticity properties. In this work, we uncover a novel characterization of EA as an optimal transport problem, allowing a natural symmetrization that can be computed efficiently using dual ascent. The corresponding novel affinity matrix derives advantages from symmetric doubly stochastic normalization in terms of clustering performance, while also effectively controlling the entropy of each row thus making it particularly robust to varying noise levels. Following, we present a new DR algorithm, SNEkhorn, that leverages this new affinity matrix. We show its clear superiority to state-of-the-art approaches with several indicators on both synthetic and real-world datasets.