Convexity in ReLU Neural Networks: beyond ICNNs?

Convex functions and their gradients play a critical role in mathematical imaging, from proximal optimization to Optimal Transport. The successes of deep learning has led many to use learning-based methods, where fixed functions or operators are replaced by learned neural networks. Regardless of their empirical superiority, establishing rigorous guarantees for these methods often requires to impose structural constraints on neural architectures, in particular convexity. The most popular way to do so is to use so-called Input Convex Neural Networks (ICNNs). In order to explore the expressivity of ICNNs, we provide necessary and sufficient conditions for a ReLU neural network to be convex. Such characterizations are based on product of weights and activations, and write nicely for any architecture in the path-lifting framework. As particular applications, we study our characterizations in depth for 1 and 2-hidden-layer neural networks: we show that every convex function implemented by a 1-hidden-layer ReLU network can be also expressed by an ICNN with the same architecture; however this property no longer holds with more layers. Finally, we provide a numerical procedure that allows an exact check of convexity for ReLU neural networks with a large number of affine regions.

PASCO (PArallel Structured COarsening): an overlay to speed up graph clustering algorithms

Clustering the nodes of a graph is a cornerstone of graph analysis and has been extensively studied. However, some popular methods are not suitable for very large graphs: e.g., spectral clustering requires the computation of the spectral decomposition of the Laplacian matrix, which is not applicable for large graphs with a large number of communities. This work introduces PASCO, an overlay that accelerates clustering algorithms. Our method consists of three steps: 1-We compute several independent small graphs representing the input graph by applying an efficient and structure-preserving coarsening algorithm. 2-A clustering algorithm is run in parallel onto each small graph and provides several partitions of the initial graph. 3-These partitions are aligned and combined with an optimal transport method to output the final partition. The PASCO framework is based on two key contributions: a novel global algorithm structure designed to enable parallelization and a fast, empirically validated graph coarsening algorithm that preserves structural properties. We demonstrate the strong performance of 1 PASCO in terms of computational efficiency, structural preservation, and output partition quality, evaluated on both synthetic and real-world graph datasets.

Path-metrics, pruning, and generalization

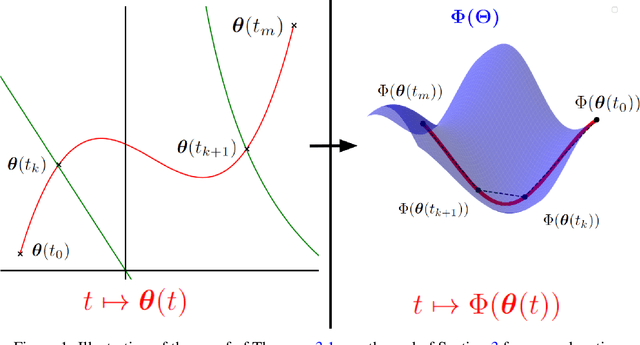
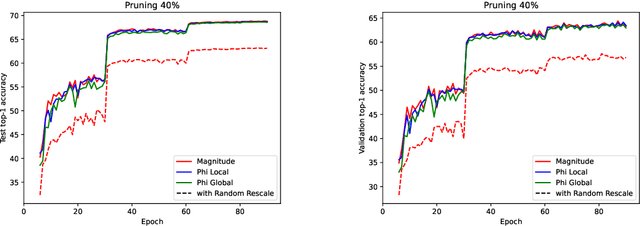
Analyzing the behavior of ReLU neural networks often hinges on understanding the relationships between their parameters and the functions they implement. This paper proves a new bound on function distances in terms of the so-called path-metrics of the parameters. Since this bound is intrinsically invariant with respect to the rescaling symmetries of the networks, it sharpens previously known bounds. It is also, to the best of our knowledge, the first bound of its kind that is broadly applicable to modern networks such as ResNets, VGGs, U-nets, and many more. In contexts such as network pruning and quantization, the proposed path-metrics can be efficiently computed using only two forward passes. Besides its intrinsic theoretical interest, the bound yields not only novel theoretical generalization bounds, but also a promising proof of concept for rescaling-invariant pruning.

Keep the Momentum: Conservation Laws beyond Euclidean Gradient Flows

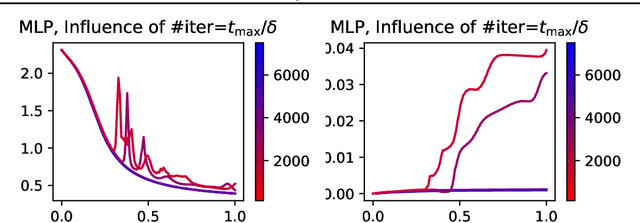
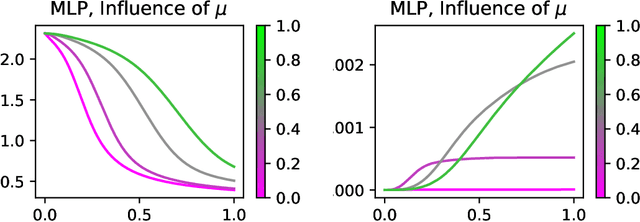
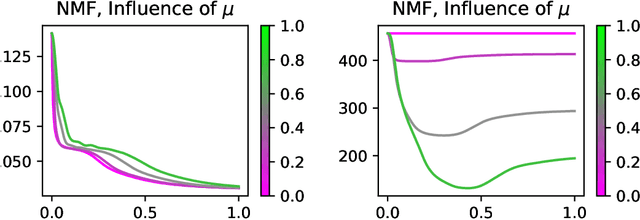
Conservation laws are well-established in the context of Euclidean gradient flow dynamics, notably for linear or ReLU neural network training. Yet, their existence and principles for non-Euclidean geometries and momentum-based dynamics remain largely unknown. In this paper, we characterize "all" conservation laws in this general setting. In stark contrast to the case of gradient flows, we prove that the conservation laws for momentum-based dynamics exhibit temporal dependence. Additionally, we often observe a "conservation loss" when transitioning from gradient flow to momentum dynamics. Specifically, for linear networks, our framework allows us to identify all momentum conservation laws, which are less numerous than in the gradient flow case except in sufficiently over-parameterized regimes. With ReLU networks, no conservation law remains. This phenomenon also manifests in non-Euclidean metrics, used e.g. for Nonnegative Matrix Factorization (NMF): all conservation laws can be determined in the gradient flow context, yet none persists in the momentum case.

Sketch and shift: a robust decoder for compressive clustering

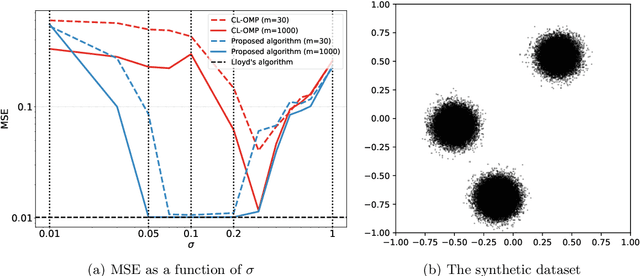
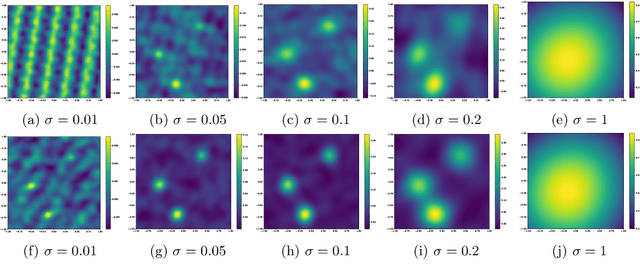
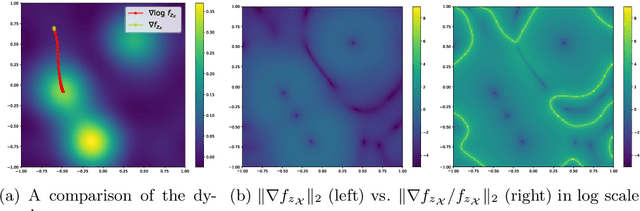
Compressive learning is an emerging approach to drastically reduce the memory footprint of large-scale learning, by first summarizing a large dataset into a low-dimensional sketch vector, and then decoding from this sketch the latent information needed for learning. In light of recent progress on information preservation guarantees for sketches based on random features, a major objective is to design easy-to-tune algorithms (called decoders) to robustly and efficiently extract this information. To address the underlying non-convex optimization problems, various heuristics have been proposed. In the case of compressive clustering, the standard heuristic is CL-OMPR, a variant of sliding Frank-Wolfe. Yet, CL-OMPR is hard to tune, and the examination of its robustness was overlooked. In this work, we undertake a scrutinized examination of CL-OMPR to circumvent its limitations. In particular, we show how this algorithm can fail to recover the clusters even in advantageous scenarios. To gain insight, we show how the deficiencies of this algorithm can be attributed to optimization difficulties related to the structure of a correlation function appearing at core steps of the algorithm. To address these limitations, we propose an alternative decoder offering substantial improvements over CL-OMPR. Its design is notably inspired from the mean shift algorithm, a classic approach to detect the local maxima of kernel density estimators. The proposed algorithm can extract clustering information from a sketch of the MNIST dataset that is 10 times smaller than previously.

Revisiting RIP guarantees for sketching operators on mixture models

In the context of sketching for compressive mixture modeling, we revisit existing proofs of the Restricted Isometry Property of sketching operators with respect to certain mixtures models. After examining the shortcomings of existing guarantees, we propose an alternative analysis that circumvents the need to assume importance sampling when drawing random Fourier features to build random sketching operators. Our analysis is based on new deterministic bounds on the restricted isometry constant that depend solely on the set of frequencies used to define the sketching operator; then we leverage these bounds to establish concentration inequalities for random sketching operators that lead to the desired RIP guarantees. Our analysis also opens the door to theoretical guarantees for structured sketching with frequencies associated to fast random linear operators.

Compressive Recovery of Sparse Precision Matrices

We consider the problem of learning a graph modeling the statistical relations of the $d$ variables of a dataset with $n$ samples $X \in \mathbb{R}^{n \times d}$. Standard approaches amount to searching for a precision matrix $\Theta$ representative of a Gaussian graphical model that adequately explains the data. However, most maximum likelihood-based estimators usually require storing the $d^{2}$ values of the empirical covariance matrix, which can become prohibitive in a high-dimensional setting. In this work, we adopt a compressive viewpoint and aim to estimate a sparse $\Theta$ from a sketch of the data, i.e. a low-dimensional vector of size $m \ll d^{2}$ carefully designed from $X$ using nonlinear random features. Under certain assumptions on the spectrum of $\Theta$ (or its condition number), we show that it is possible to estimate it from a sketch of size $m=\Omega((d+2k)\log(d))$ where $k$ is the maximal number of edges of the underlying graph. These information-theoretic guarantees are inspired by compressed sensing theory and involve restricted isometry properties and instance optimal decoders. We investigate the possibility of achieving practical recovery with an iterative algorithm based on the graphical lasso, viewed as a specific denoiser. We compare our approach and graphical lasso on synthetic datasets, demonstrating its favorable performance even when the dataset is compressed.

A path-norm toolkit for modern networks: consequences, promises and challenges

This work introduces the first toolkit around path-norms that is fully able to encompass general DAG ReLU networks with biases, skip connections and any operation based on the extraction of order statistics: max pooling, GroupSort etc. This toolkit notably allows us to establish generalization bounds for modern neural networks that are not only the most widely applicable path-norm based ones, but also recover or beat the sharpest known bounds of this type. These extended path-norms further enjoy the usual benefits of path-norms: ease of computation, invariance under the symmetries of the network, and improved sharpness on feedforward networks compared to the product of operators' norms, another complexity measure most commonly used. The versatility of the toolkit and its ease of implementation allow us to challenge the concrete promises of path-norm-based generalization bounds, by numerically evaluating the sharpest known bounds for ResNets on ImageNet.

Abide by the Law and Follow the Flow: Conservation Laws for Gradient Flows

Understanding the geometric properties of gradient descent dynamics is a key ingredient in deciphering the recent success of very large machine learning models. A striking observation is that trained over-parameterized models retain some properties of the optimization initialization. This "implicit bias" is believed to be responsible for some favorable properties of the trained models and could explain their good generalization properties. The purpose of this article is threefold. First, we rigorously expose the definition and basic properties of "conservation laws", which are maximal sets of independent quantities conserved during gradient flows of a given model (e.g. of a ReLU network with a given architecture) with any training data and any loss. Then we explain how to find the exact number of these quantities by performing finite-dimensional algebraic manipulations on the Lie algebra generated by the Jacobian of the model. Finally, we provide algorithms (implemented in SageMath) to: a) compute a family of polynomial laws; b) compute the number of (not necessarily polynomial) conservation laws. We provide showcase examples that we fully work out theoretically. Besides, applying the two algorithms confirms for a number of ReLU network architectures that all known laws are recovered by the algorithm, and that there are no other laws. Such computational tools pave the way to understanding desirable properties of optimization initialization in large machine learning models.

About the Cost of Global Privacy in Density Estimation

We study non-parametric density estimation for densities in Lipschitz and Sobolev spaces, and under global privacy. In particular, we investigate regimes where the privacy budget is not supposed to be constant. We consider the classical definition of global differential privacy, but also the more recent notion of global concentrated differential privacy. We recover the result of Barber \& Duchi (2014) stating that histogram estimators are optimal against Lipschitz distributions for the L2 risk, and under regular differential privacy, and we extend it to other norms and notions of privacy. Then, we investigate higher degrees of smoothness, drawing two conclusions: First, and contrary to what happens with constant privacy budget (Wasserman \& Zhou, 2010), there are regimes where imposing privacy degrades the regular minimax risk of estimation on Sobolev densities. Second, so-called projection estimators are near-optimal against the same classes of densities in this new setup with pure differential privacy, but contrary to the constant privacy budget case, it comes at the cost of relaxation. With zero concentrated differential privacy, there is no need for relaxation, and we prove that the estimation is optimal.