Path-metrics, pruning, and generalization

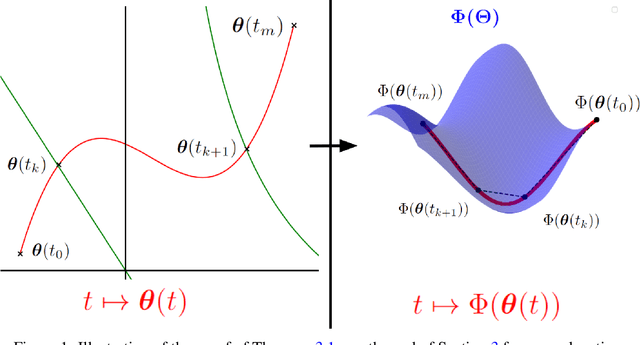
Analyzing the behavior of ReLU neural networks often hinges on understanding the relationships between their parameters and the functions they implement. This paper proves a new bound on function distances in terms of the so-called path-metrics of the parameters. Since this bound is intrinsically invariant with respect to the rescaling symmetries of the networks, it sharpens previously known bounds. It is also, to the best of our knowledge, the first bound of its kind that is broadly applicable to modern networks such as ResNets, VGGs, U-nets, and many more. In contexts such as network pruning and quantization, the proposed path-metrics can be efficiently computed using only two forward passes. Besides its intrinsic theoretical interest, the bound yields not only novel theoretical generalization bounds, but also a promising proof of concept for rescaling-invariant pruning.

Make Inference Faster: Efficient GPU Memory Management for Butterfly Sparse Matrix Multiplication

This paper is the first to assess the state of existing sparse matrix multiplication algorithms on GPU for the butterfly structure, a promising form of sparsity. This is achieved through a comprehensive benchmark that can be easily modified to add a new implementation. The goal is to provide a simple tool for users to select the optimal implementation based on their settings. Using this benchmark, we find that existing implementations spend up to 50% of their total runtime on memory rewriting operations. We show that these memory operations can be optimized by introducing a new CUDA kernel that minimizes the transfers between the different levels of GPU memory, achieving a median speed-up factor of x1.4 while also reducing energy consumption (median of x0.85). We also demonstrate the broader significance of our results by showing how the new kernel can speed up the inference of neural networks.

A path-norm toolkit for modern networks: consequences, promises and challenges

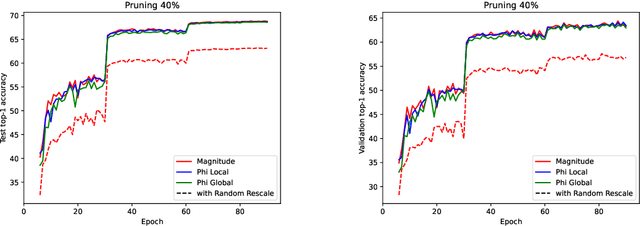
This work introduces the first toolkit around path-norms that is fully able to encompass general DAG ReLU networks with biases, skip connections and any operation based on the extraction of order statistics: max pooling, GroupSort etc. This toolkit notably allows us to establish generalization bounds for modern neural networks that are not only the most widely applicable path-norm based ones, but also recover or beat the sharpest known bounds of this type. These extended path-norms further enjoy the usual benefits of path-norms: ease of computation, invariance under the symmetries of the network, and improved sharpness on feedforward networks compared to the product of operators' norms, another complexity measure most commonly used. The versatility of the toolkit and its ease of implementation allow us to challenge the concrete promises of path-norm-based generalization bounds, by numerically evaluating the sharpest known bounds for ResNets on ImageNet.

Sparsity in neural networks can improve their privacy

This article measures how sparsity can make neural networks more robust to membership inference attacks. The obtained empirical results show that sparsity improves the privacy of the network, while preserving comparable performances on the task at hand. This empirical study completes and extends existing literature.

Sparsity in neural networks can increase their privacy

This article measures how sparsity can make neural networks more robust to membership inference attacks. The obtained empirical results show that sparsity improves the privacy of the network, while preserving comparable performances on the task at hand. This empirical study completes and extends existing literature.

Approximation speed of quantized vs. unquantized ReLU neural networks and beyond

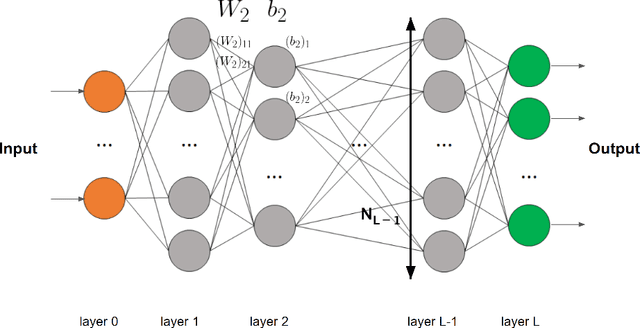
We consider general approximation families encompassing ReLU neural networks. On the one hand, we introduce a new property, that we call $\infty$-encodability, which lays a framework that we use (i) to guarantee that ReLU networks can be uniformly quantized and still have approximation speeds comparable to unquantized ones, and (ii) to prove that ReLU networks share a common limitation with many other approximation families: the approximation speed of a set C is bounded from above by an encoding complexity of C (a complexity well-known for many C's). The property of $\infty$-encodability allows us to unify and generalize known results in which it was implicitly used. On the other hand, we give lower and upper bounds on the Lipschitz constant of the mapping that associates the weights of a network to the function they represent in L^p. It is given in terms of the width, the depth of the network and a bound on the weight's norm, and it is based on well-known upper bounds on the Lipschitz constants of the functions represented by ReLU networks. This allows us to recover known results, to establish new bounds on covering numbers, and to characterize the accuracy of naive uniform quantization of ReLU networks.

Compressive Learning for Semi-Parametric Models

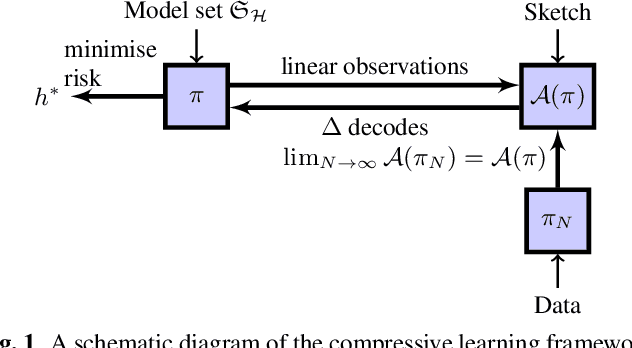
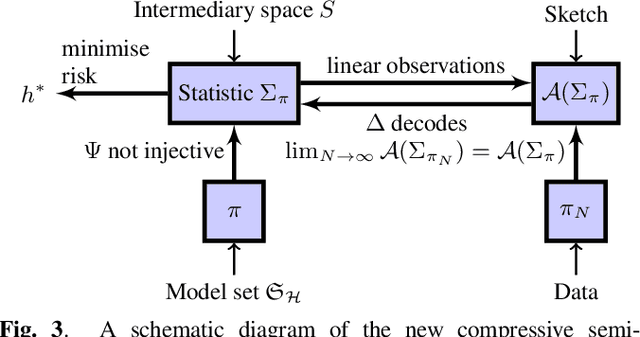
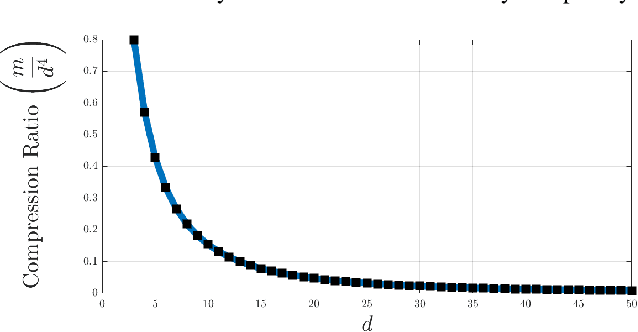
In the compressive learning theory, instead of solving a statistical learning problem from the input data, a so-called sketch is computed from the data prior to learning. The sketch has to capture enough information to solve the problem directly from it, allowing to discard the dataset from the memory. This is useful when dealing with large datasets as the size of the sketch does not scale with the size of the database. In this paper, we reformulate the original compressive learning framework to explicitly cater for the class of semi-parametric models. The reformulation takes account of the inherent topology and structure of semi-parametric models, creating an intuitive pathway to the development of compressive learning algorithms. We apply our developed framework to both the semi-parametric models of independent component analysis and subspace clustering, demonstrating the robustness of the framework to explicitly show when a compression in complexity can be achieved.