Approximation speed of quantized vs. unquantized ReLU neural networks and beyond
Paper and Code
May 24, 2022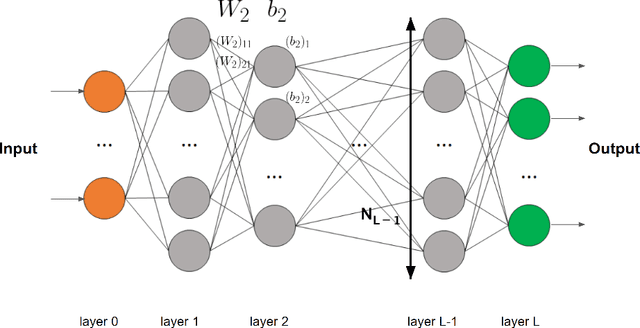
We consider general approximation families encompassing ReLU neural networks. On the one hand, we introduce a new property, that we call $\infty$-encodability, which lays a framework that we use (i) to guarantee that ReLU networks can be uniformly quantized and still have approximation speeds comparable to unquantized ones, and (ii) to prove that ReLU networks share a common limitation with many other approximation families: the approximation speed of a set C is bounded from above by an encoding complexity of C (a complexity well-known for many C's). The property of $\infty$-encodability allows us to unify and generalize known results in which it was implicitly used. On the other hand, we give lower and upper bounds on the Lipschitz constant of the mapping that associates the weights of a network to the function they represent in L^p. It is given in terms of the width, the depth of the network and a bound on the weight's norm, and it is based on well-known upper bounds on the Lipschitz constants of the functions represented by ReLU networks. This allows us to recover known results, to establish new bounds on covering numbers, and to characterize the accuracy of naive uniform quantization of ReLU networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge