Path-metrics, pruning, and generalization

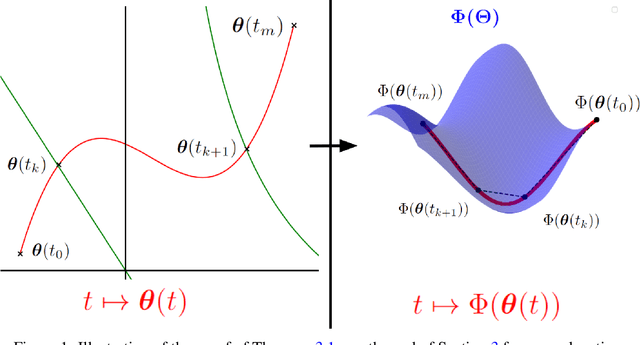
Analyzing the behavior of ReLU neural networks often hinges on understanding the relationships between their parameters and the functions they implement. This paper proves a new bound on function distances in terms of the so-called path-metrics of the parameters. Since this bound is intrinsically invariant with respect to the rescaling symmetries of the networks, it sharpens previously known bounds. It is also, to the best of our knowledge, the first bound of its kind that is broadly applicable to modern networks such as ResNets, VGGs, U-nets, and many more. In contexts such as network pruning and quantization, the proposed path-metrics can be efficiently computed using only two forward passes. Besides its intrinsic theoretical interest, the bound yields not only novel theoretical generalization bounds, but also a promising proof of concept for rescaling-invariant pruning.

A path-norm toolkit for modern networks: consequences, promises and challenges

This work introduces the first toolkit around path-norms that is fully able to encompass general DAG ReLU networks with biases, skip connections and any operation based on the extraction of order statistics: max pooling, GroupSort etc. This toolkit notably allows us to establish generalization bounds for modern neural networks that are not only the most widely applicable path-norm based ones, but also recover or beat the sharpest known bounds of this type. These extended path-norms further enjoy the usual benefits of path-norms: ease of computation, invariance under the symmetries of the network, and improved sharpness on feedforward networks compared to the product of operators' norms, another complexity measure most commonly used. The versatility of the toolkit and its ease of implementation allow us to challenge the concrete promises of path-norm-based generalization bounds, by numerically evaluating the sharpest known bounds for ResNets on ImageNet.

Does a sparse ReLU network training problem always admit an optimum?

Given a training set, a loss function, and a neural network architecture, it is often taken for granted that optimal network parameters exist, and a common practice is to apply available optimization algorithms to search for them. In this work, we show that the existence of an optimal solution is not always guaranteed, especially in the context of {\em sparse} ReLU neural networks. In particular, we first show that optimization problems involving deep networks with certain sparsity patterns do not always have optimal parameters, and that optimization algorithms may then diverge. Via a new topological relation between sparse ReLU neural networks and their linear counterparts, we derive -- using existing tools from real algebraic geometry -- an algorithm to verify that a given sparsity pattern suffers from this issue. Then, the existence of a global optimum is proved for every concrete optimization problem involving a shallow sparse ReLU neural network of output dimension one. Overall, the analysis is based on the investigation of two topological properties of the space of functions implementable as sparse ReLU neural networks: a best approximation property, and a closedness property, both in the uniform norm. This is studied both for (finite) domains corresponding to practical training on finite training sets, and for more general domains such as the unit cube. This allows us to provide conditions for the guaranteed existence of an optimum given a sparsity pattern. The results apply not only to several sparsity patterns proposed in recent works on network pruning/sparsification, but also to classical dense neural networks, including architectures not covered by existing results.

A Block-Coordinate Approach of Multi-level Optimization with an Application to Physics-Informed Neural Networks

Multi-level methods are widely used for the solution of large-scale problems, because of their computational advantages and exploitation of the complementarity between the involved sub-problems. After a re-interpretation of multi-level methods from a block-coordinate point of view, we propose a multi-level algorithm for the solution of nonlinear optimization problems and analyze its evaluation complexity. We apply it to the solution of partial differential equations using physics-informed neural networks (PINNs) and show on a few test problems that the approach results in better solutions and significant computational savings

Self-supervised learning with rotation-invariant kernels

A major paradigm for learning image representations in a self-supervised manner is to learn a model that is invariant to some predefined image transformations (cropping, blurring, color jittering, etc.), while regularizing the embedding distribution to avoid learning a degenerate solution. Our first contribution is to propose a general kernel framework to design a generic regularization loss that promotes the embedding distribution to be close to the uniform distribution on the hypersphere, with respect to the maximum mean discrepancy pseudometric. Our framework uses rotation-invariant kernels defined on the hypersphere, also known as dot-product kernels. Our second contribution is to show that this flexible kernel approach encompasses several existing self-supervised learning methods, including uniformity-based and information-maximization methods. Finally, by exploring empirically several kernel choices, our experiments demonstrate that using a truncated rotation-invariant kernel provides competitive results compared to state-of-the-art methods, and we show practical situations where our method benefits from the kernel trick to reduce computational complexity.

Approximation speed of quantized vs. unquantized ReLU neural networks and beyond

We consider general approximation families encompassing ReLU neural networks. On the one hand, we introduce a new property, that we call $\infty$-encodability, which lays a framework that we use (i) to guarantee that ReLU networks can be uniformly quantized and still have approximation speeds comparable to unquantized ones, and (ii) to prove that ReLU networks share a common limitation with many other approximation families: the approximation speed of a set C is bounded from above by an encoding complexity of C (a complexity well-known for many C's). The property of $\infty$-encodability allows us to unify and generalize known results in which it was implicitly used. On the other hand, we give lower and upper bounds on the Lipschitz constant of the mapping that associates the weights of a network to the function they represent in L^p. It is given in terms of the width, the depth of the network and a bound on the weight's norm, and it is based on well-known upper bounds on the Lipschitz constants of the functions represented by ReLU networks. This allows us to recover known results, to establish new bounds on covering numbers, and to characterize the accuracy of naive uniform quantization of ReLU networks.

Identifiability in Exact Two-Layer Sparse Matrix Factorization

Sparse matrix factorization is the problem of approximating a matrix Z by a product of L sparse factors X^(L) X^(L--1). .. X^(1). This paper focuses on identifiability issues that appear in this problem, in view of better understanding under which sparsity constraints the problem is well-posed. We give conditions under which the problem of factorizing a matrix into two sparse factors admits a unique solution, up to unavoidable permutation and scaling equivalences. Our general framework considers an arbitrary family of prescribed sparsity patterns, allowing us to capture more structured notions of sparsity than simply the count of nonzero entries. These conditions are shown to be related to essential uniqueness of exact matrix decomposition into a sum of rank-one matrices, with structured sparsity constraints. A companion paper further exploits these conditions to derive identifiability properties in multilayer sparse matrix factorization of some well-known matrices like the Hadamard or the discrete Fourier transform matrices.

Identifiability in Exact Multilayer Sparse Matrix Factorization

Many well-known matrices Z are associated to fast transforms corresponding to factorizations of the form Z = X^(L). .. X^(1) , where each factor X^(l) is sparse. Based on general result for the case with two factors, established in a companion paper, we investigate essential uniqueness of such factorizations. We show some identifiability results for the sparse factorization into two factors of the discrete Fourier Transform, discrete cosine transform or discrete sine transform matrices of size N = 2^L , when enforcing N/2-sparsity by column on the left factor, and 2-sparsity by row on the right factor. We also show that the analysis with two factors can be extended to the multilayer case, based on a hierarchical factorization method. We prove that any matrix which is the product of L factors whose supports are exactly the so-called butterfly supports, admits a unique sparse factorization into L factors. This applies in particular to the Hadamard or the discrete Fourier transform matrix of size 2^L .

On the approximation of the solution of partial differential equations by artificial neural networks trained by a multilevel Levenberg-Marquardt method

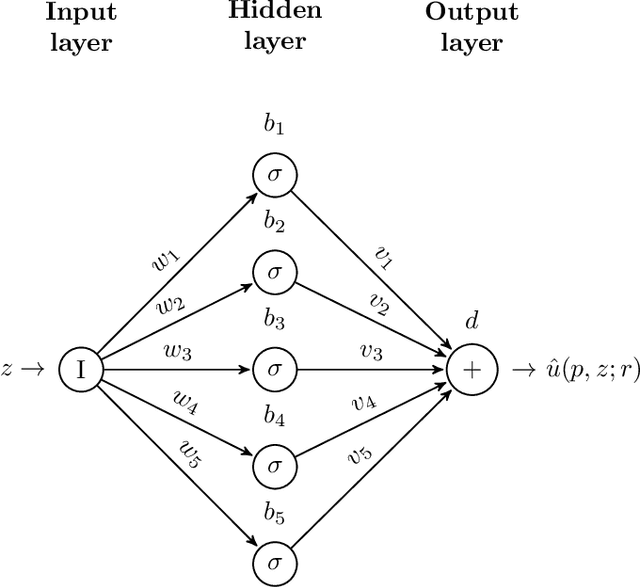
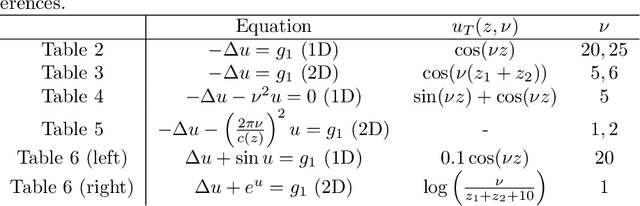
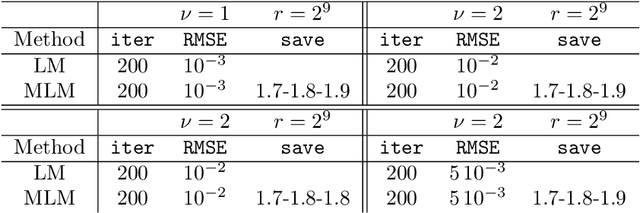
This paper is concerned with the approximation of the solution of partial differential equations by means of artificial neural networks. Here a feedforward neural network is used to approximate the solution of the partial differential equation. The learning problem is formulated as a least squares problem, choosing the residual of the partial differential equation as a loss function, whereas a multilevel Levenberg-Marquardt method is employed as a training method. This setting allows us to get further insight into the potential of multilevel methods. Indeed, when the least squares problem arises from the training of artificial neural networks, the variables subject to optimization are not related by any geometrical constraints and the standard interpolation and restriction operators cannot be employed any longer. A heuristic, inspired by algebraic multigrid methods, is then proposed to construct the multilevel transfer operators. Numerical experiments show encouraging results related to the efficiency of the new multilevel optimization method for the training of artificial neural networks, compared to the standard corresponding one-level procedure.