On the approximation of the solution of partial differential equations by artificial neural networks trained by a multilevel Levenberg-Marquardt method

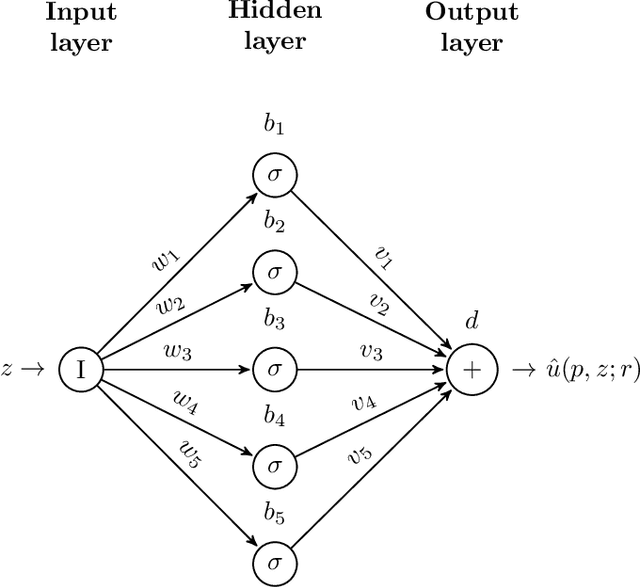
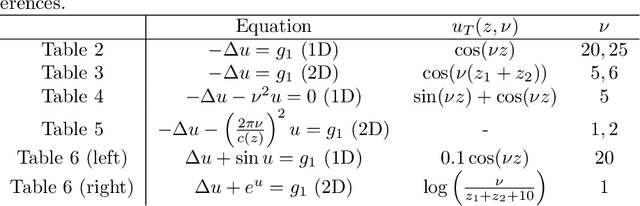
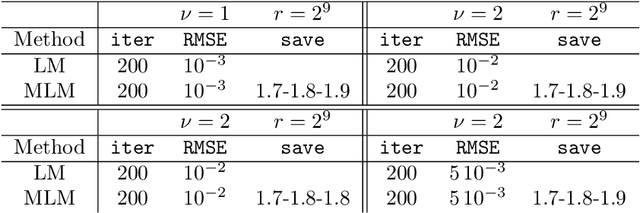
This paper is concerned with the approximation of the solution of partial differential equations by means of artificial neural networks. Here a feedforward neural network is used to approximate the solution of the partial differential equation. The learning problem is formulated as a least squares problem, choosing the residual of the partial differential equation as a loss function, whereas a multilevel Levenberg-Marquardt method is employed as a training method. This setting allows us to get further insight into the potential of multilevel methods. Indeed, when the least squares problem arises from the training of artificial neural networks, the variables subject to optimization are not related by any geometrical constraints and the standard interpolation and restriction operators cannot be employed any longer. A heuristic, inspired by algebraic multigrid methods, is then proposed to construct the multilevel transfer operators. Numerical experiments show encouraging results related to the efficiency of the new multilevel optimization method for the training of artificial neural networks, compared to the standard corresponding one-level procedure.