Serge Gratton
Recursive Bound-Constrained AdaGrad with Applications to Multilevel and Domain Decomposition Minimization
Jul 15, 2025Abstract:Two OFFO (Objective-Function Free Optimization) noise tolerant algorithms are presented that handle bound constraints, inexact gradients and use second-order information when available.The first is a multi-level method exploiting a hierarchical description of the problem and the second is a domain-decomposition method covering the standard addditive Schwarz decompositions. Both are generalizations of the first-order AdaGrad algorithm for unconstrained optimization. Because these algorithms share a common theoretical framework, a single convergence/complexity theory is provided which covers them both. Its main result is that, with high probability, both methods need at most $O(\epsilon^{-2})$ iterations and noisy gradient evaluations to compute an $\epsilon$-approximate first-order critical point of the bound-constrained problem. Extensive numerical experiments are discussed on applications ranging from PDE-based problems to deep neural network training, illustrating their remarkable computational efficiency.
Feature Representation Transferring to Lightweight Models via Perception Coherence
May 10, 2025Abstract:In this paper, we propose a method for transferring feature representation to lightweight student models from larger teacher models. We mathematically define a new notion called \textit{perception coherence}. Based on this notion, we propose a loss function, which takes into account the dissimilarities between data points in feature space through their ranking. At a high level, by minimizing this loss function, the student model learns to mimic how the teacher model \textit{perceives} inputs. More precisely, our method is motivated by the fact that the representational capacity of the student model is weaker than the teacher model. Hence, we aim to develop a new method allowing for a better relaxation. This means that, the student model does not need to preserve the absolute geometry of the teacher one, while preserving global coherence through dissimilarity ranking. Our theoretical insights provide a probabilistic perspective on the process of feature representation transfer. Our experiments results show that our method outperforms or achieves on-par performance compared to strong baseline methods for representation transferring.
Convolutional Rectangular Attention Module
Mar 13, 2025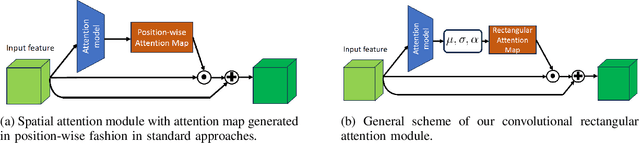
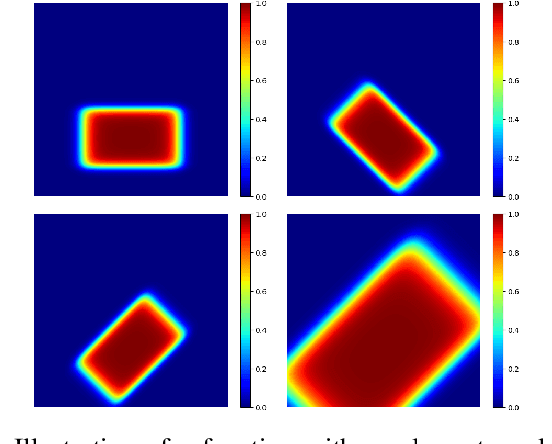
Abstract:In this paper, we introduce a novel spatial attention module, that can be integrated to any convolutional network. This module guides the model to pay attention to the most discriminative part of an image. This enables the model to attain a better performance by an end-to-end training. In standard approaches, a spatial attention map is generated in a position-wise fashion. We observe that this results in very irregular boundaries. This could make it difficult to generalize to new samples. In our method, the attention region is constrained to be rectangular. This rectangle is parametrized by only 5 parameters, allowing for a better stability and generalization to new samples. In our experiments, our method systematically outperforms the position-wise counterpart. Thus, this provides us a novel useful spatial attention mechanism for convolutional models. Besides, our module also provides the interpretability concerning the ``where to look" question, as it helps to know the part of the input on which the model focuses to produce the prediction.
Two-level deep domain decomposition method
Aug 22, 2024Abstract:This study presents a two-level Deep Domain Decomposition Method (Deep-DDM) augmented with a coarse-level network for solving boundary value problems using physics-informed neural networks (PINNs). The addition of the coarse level network improves scalability and convergence rates compared to the single level method. Tested on a Poisson equation with Dirichlet boundary conditions, the two-level deep DDM demonstrates superior performance, maintaining efficient convergence regardless of the number of subdomains. This advance provides a more scalable and effective approach to solving complex partial differential equations with machine learning.
Large Margin Discriminative Loss for Classification
May 28, 2024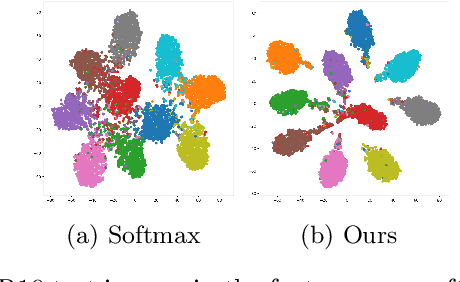
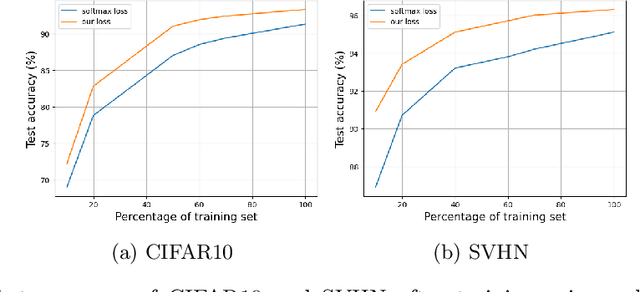
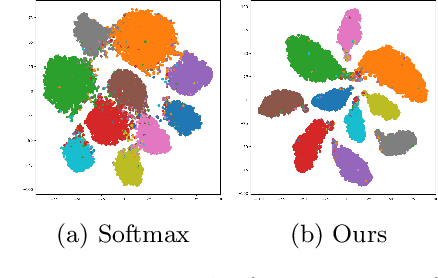
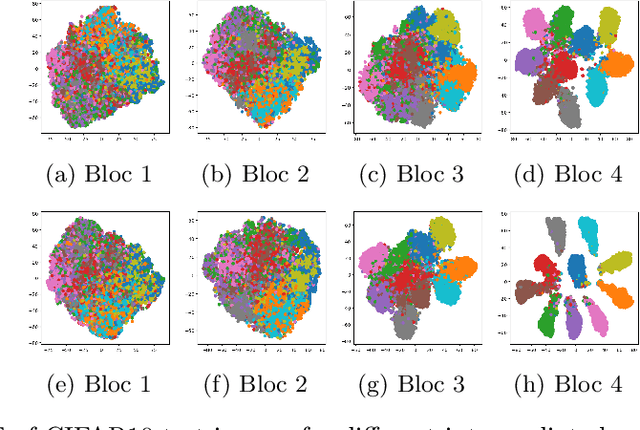
Abstract:In this paper, we introduce a novel discriminative loss function with large margin in the context of Deep Learning. This loss boosts the discriminative power of neural nets, represented by intra-class compactness and inter-class separability. On the one hand, the class compactness is ensured by close distance of samples of the same class to each other. On the other hand, the inter-class separability is boosted by a margin loss that ensures the minimum distance of each class to its closest boundary. All the terms in our loss have an explicit meaning, giving a direct view of the feature space obtained. We analyze mathematically the relation between compactness and margin term, giving a guideline about the impact of the hyper-parameters on the learned features. Moreover, we also analyze properties of the gradient of the loss with respect to the parameters of the neural net. Based on this, we design a strategy called partial momentum updating that enjoys simultaneously stability and consistency in training. Furthermore, we also investigate generalization errors to have better theoretical insights. Our loss function systematically boosts the test accuracy of models compared to the standard softmax loss in our experiments.
Combining Statistical Depth and Fermat Distance for Uncertainty Quantification
Apr 12, 2024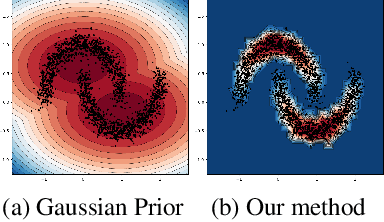
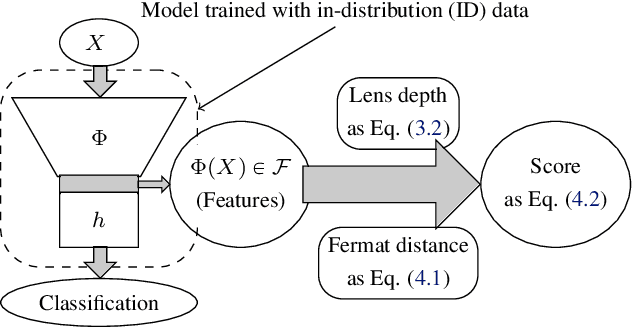
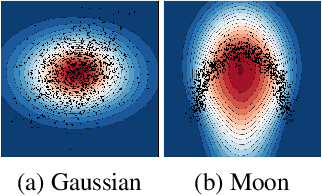
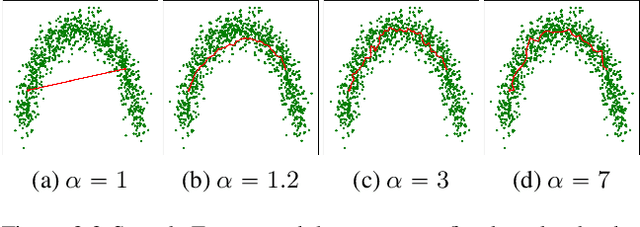
Abstract:We measure the Out-of-domain uncertainty in the prediction of Neural Networks using a statistical notion called ``Lens Depth'' (LD) combined with Fermat Distance, which is able to capture precisely the ``depth'' of a point with respect to a distribution in feature space, without any assumption about the form of distribution. Our method has no trainable parameter. The method is applicable to any classification model as it is applied directly in feature space at test time and does not intervene in training process. As such, it does not impact the performance of the original model. The proposed method gives excellent qualitative result on toy datasets and can give competitive or better uncertainty estimation on standard deep learning datasets compared to strong baseline methods.
A Block-Coordinate Approach of Multi-level Optimization with an Application to Physics-Informed Neural Networks
May 25, 2023Abstract:Multi-level methods are widely used for the solution of large-scale problems, because of their computational advantages and exploitation of the complementarity between the involved sub-problems. After a re-interpretation of multi-level methods from a block-coordinate point of view, we propose a multi-level algorithm for the solution of nonlinear optimization problems and analyze its evaluation complexity. We apply it to the solution of partial differential equations using physics-informed neural networks (PINNs) and show on a few test problems that the approach results in better solutions and significant computational savings
A coarse space acceleration of deep-DDM
Dec 07, 2021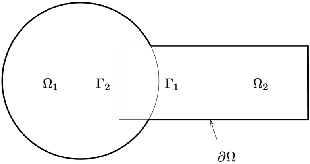



Abstract:The use of deep learning methods for solving PDEs is a field in full expansion. In particular, Physical Informed Neural Networks, that implement a sampling of the physical domain and use a loss function that penalizes the violation of the partial differential equation, have shown their great potential. Yet, to address large scale problems encountered in real applications and compete with existing numerical methods for PDEs, it is important to design parallel algorithms with good scalability properties. In the vein of traditional domain decomposition methods (DDM), we consider the recently proposed deep-ddm approach. We present an extension of this method that relies on the use of a coarse space correction, similarly to what is done in traditional DDM solvers. Our investigations shows that the coarse correction is able to alleviate the deterioration of the convergence of the solver when the number of subdomains is increased thanks to an instantaneous information exchange between subdomains at each iteration. Experimental results demonstrate that our approach induces a remarkable acceleration of the original deep-ddm method, at a reduced additional computational cost.
Latent Space Data Assimilation by using Deep Learning
Apr 01, 2021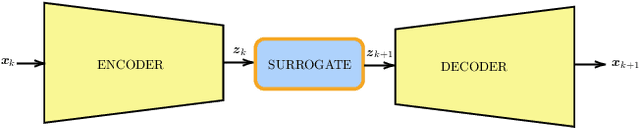
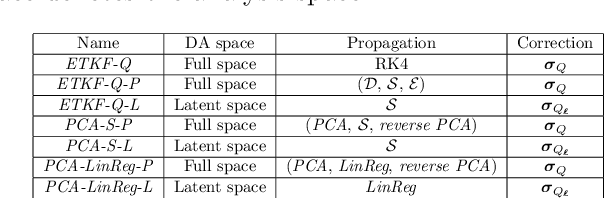
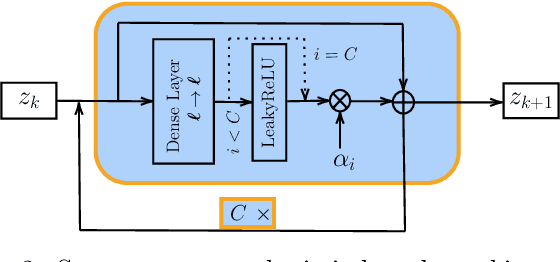
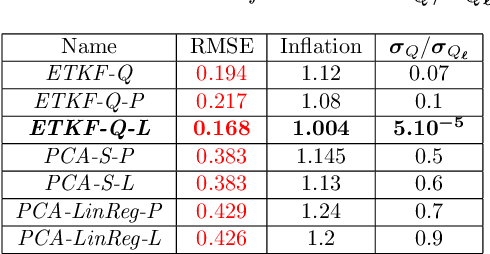
Abstract:Performing Data Assimilation (DA) at a low cost is of prime concern in Earth system modeling, particularly at the time of big data where huge quantities of observations are available. Capitalizing on the ability of Neural Networks techniques for approximating the solution of PDE's, we incorporate Deep Learning (DL) methods into a DA framework. More precisely, we exploit the latent structure provided by autoencoders (AEs) to design an Ensemble Transform Kalman Filter with model error (ETKF-Q) in the latent space. Model dynamics are also propagated within the latent space via a surrogate neural network. This novel ETKF-Q-Latent (thereafter referred to as ETKF-Q-L) algorithm is tested on a tailored instructional version of Lorenz 96 equations, named the augmented Lorenz 96 system: it possesses a latent structure that accurately represents the observed dynamics. Numerical experiments based on this particular system evidence that the ETKF-Q-L approach both reduces the computational cost and provides better accuracy than state of the art algorithms, such as the ETKF-Q.
DAN -- An optimal Data Assimilation framework based on machine learning Recurrent Networks
Oct 19, 2020



Abstract:Data assimilation algorithms aim at forecasting the state of a dynamical system by combining a mathematical representation of the system with noisy observations thereof. We propose a fully data driven deep learning architecture generalizing recurrent Elman networks and data assimilation algorithms which provably reaches the same prediction goals as the latter. On numerical experiments based on the well-known Lorenz system and when suitably trained using snapshots of the system trajectory (i.e. batches of state trajectories) and observations, our architecture successfully reconstructs both the analysis and the propagation of probability density functions of the system state at a given time conditioned to past observations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge