Feature Representation Transferring to Lightweight Models via Perception Coherence

In this paper, we propose a method for transferring feature representation to lightweight student models from larger teacher models. We mathematically define a new notion called \textit{perception coherence}. Based on this notion, we propose a loss function, which takes into account the dissimilarities between data points in feature space through their ranking. At a high level, by minimizing this loss function, the student model learns to mimic how the teacher model \textit{perceives} inputs. More precisely, our method is motivated by the fact that the representational capacity of the student model is weaker than the teacher model. Hence, we aim to develop a new method allowing for a better relaxation. This means that, the student model does not need to preserve the absolute geometry of the teacher one, while preserving global coherence through dissimilarity ranking. Our theoretical insights provide a probabilistic perspective on the process of feature representation transfer. Our experiments results show that our method outperforms or achieves on-par performance compared to strong baseline methods for representation transferring.

Convolutional Rectangular Attention Module

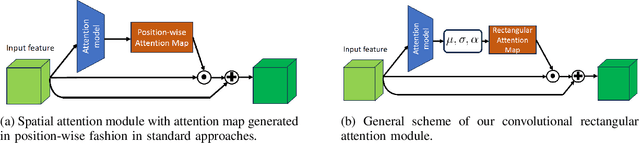
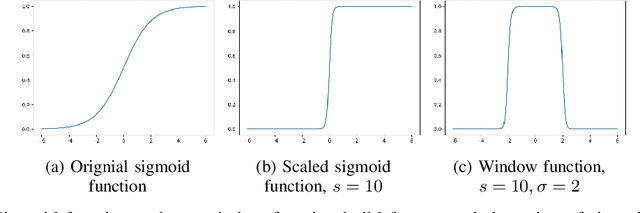
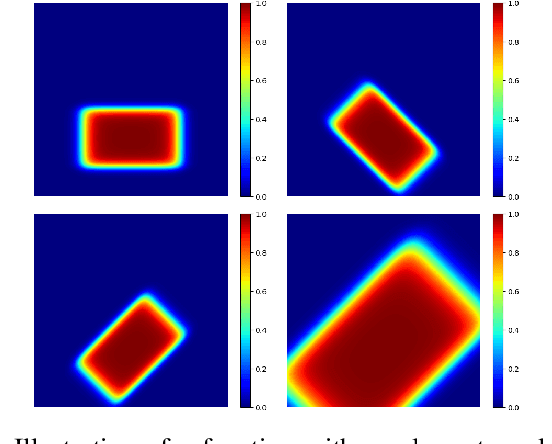
In this paper, we introduce a novel spatial attention module, that can be integrated to any convolutional network. This module guides the model to pay attention to the most discriminative part of an image. This enables the model to attain a better performance by an end-to-end training. In standard approaches, a spatial attention map is generated in a position-wise fashion. We observe that this results in very irregular boundaries. This could make it difficult to generalize to new samples. In our method, the attention region is constrained to be rectangular. This rectangle is parametrized by only 5 parameters, allowing for a better stability and generalization to new samples. In our experiments, our method systematically outperforms the position-wise counterpart. Thus, this provides us a novel useful spatial attention mechanism for convolutional models. Besides, our module also provides the interpretability concerning the ``where to look" question, as it helps to know the part of the input on which the model focuses to produce the prediction.

Large Margin Discriminative Loss for Classification

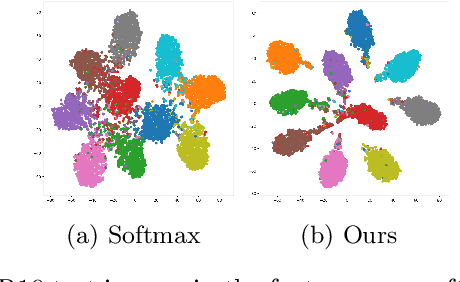
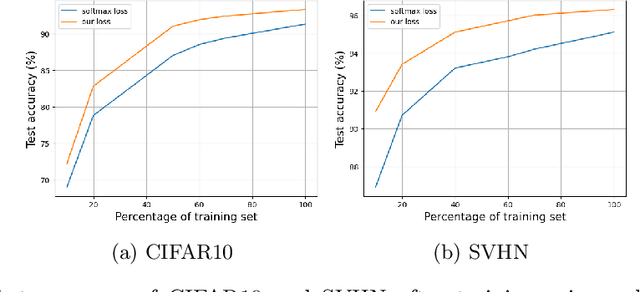
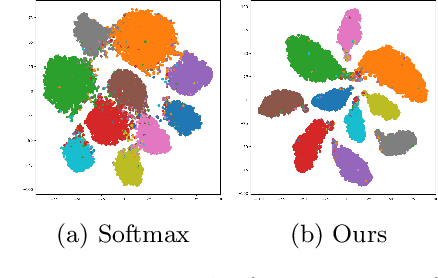
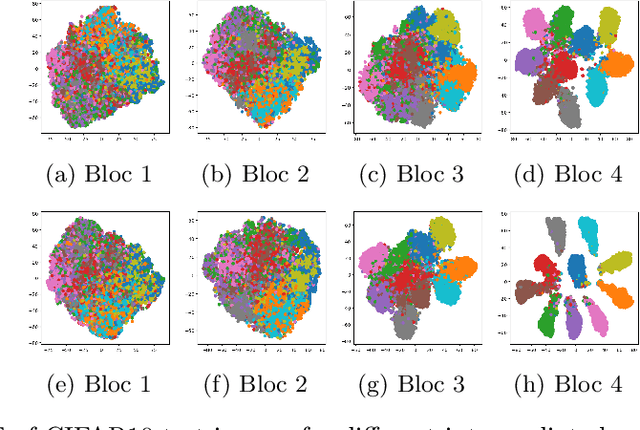
In this paper, we introduce a novel discriminative loss function with large margin in the context of Deep Learning. This loss boosts the discriminative power of neural nets, represented by intra-class compactness and inter-class separability. On the one hand, the class compactness is ensured by close distance of samples of the same class to each other. On the other hand, the inter-class separability is boosted by a margin loss that ensures the minimum distance of each class to its closest boundary. All the terms in our loss have an explicit meaning, giving a direct view of the feature space obtained. We analyze mathematically the relation between compactness and margin term, giving a guideline about the impact of the hyper-parameters on the learned features. Moreover, we also analyze properties of the gradient of the loss with respect to the parameters of the neural net. Based on this, we design a strategy called partial momentum updating that enjoys simultaneously stability and consistency in training. Furthermore, we also investigate generalization errors to have better theoretical insights. Our loss function systematically boosts the test accuracy of models compared to the standard softmax loss in our experiments.

Combining Statistical Depth and Fermat Distance for Uncertainty Quantification

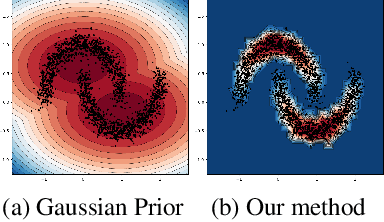
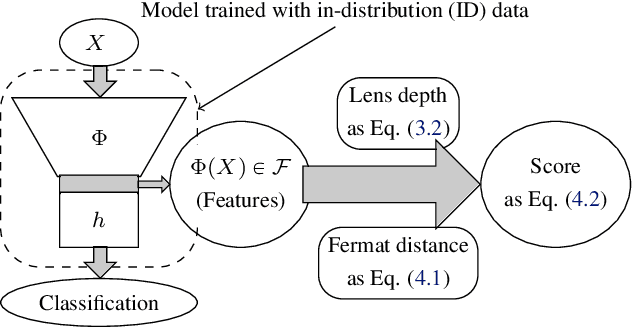
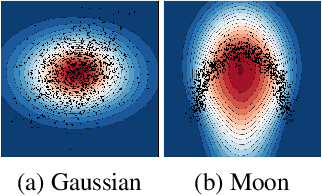
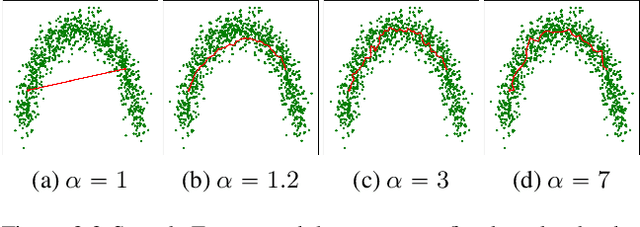
We measure the Out-of-domain uncertainty in the prediction of Neural Networks using a statistical notion called ``Lens Depth'' (LD) combined with Fermat Distance, which is able to capture precisely the ``depth'' of a point with respect to a distribution in feature space, without any assumption about the form of distribution. Our method has no trainable parameter. The method is applicable to any classification model as it is applied directly in feature space at test time and does not intervene in training process. As such, it does not impact the performance of the original model. The proposed method gives excellent qualitative result on toy datasets and can give competitive or better uncertainty estimation on standard deep learning datasets compared to strong baseline methods.