Explaining Models under Multivariate Bernoulli Distribution via Hoeffding Decomposition

Explaining the behavior of predictive models with random inputs can be achieved through sub-models decomposition, where such sub-models have easier interpretable features. Arising from the uncertainty quantification community, recent results have demonstrated the existence and uniqueness of a generalized Hoeffding decomposition for such predictive models when the stochastic input variables are correlated, based on concepts of oblique projection onto L 2 subspaces. This article focuses on the case where the input variables have Bernoulli distributions and provides a complete description of this decomposition. We show that in this case the underlying L 2 subspaces are one-dimensional and that the functional decomposition is explicit. This leads to a complete interpretability framework and theoretically allows reverse engineering. Explicit indicators of the influence of inputs on the output prediction (exemplified by Sobol' indices and Shapley effects) can be explicitly derived. Illustrated by numerical experiments, this type of analysis proves useful for addressing decision-support problems, based on binary decision diagrams, Boolean networks or binary neural networks. The article outlines perspectives for exploring high-dimensional settings and, beyond the case of binary inputs, extending these findings to models with finite countable inputs.

Non-asymptotic confidence regions on RKHS. The Paley-Wiener and standard Sobolev space cases

We consider the problem of constructing a global, probabilistic, and non-asymptotic confidence region for an unknown function observed on a random design. The unknown function is assumed to lie in a reproducing kernel Hilbert space (RKHS). We show that this construction can be reduced to accurately estimating the RKHS norm of the unknown function. Our analysis primarily focuses both on the Paley-Wiener and on the standard Sobolev space settings.

Feature Representation Transferring to Lightweight Models via Perception Coherence

In this paper, we propose a method for transferring feature representation to lightweight student models from larger teacher models. We mathematically define a new notion called \textit{perception coherence}. Based on this notion, we propose a loss function, which takes into account the dissimilarities between data points in feature space through their ranking. At a high level, by minimizing this loss function, the student model learns to mimic how the teacher model \textit{perceives} inputs. More precisely, our method is motivated by the fact that the representational capacity of the student model is weaker than the teacher model. Hence, we aim to develop a new method allowing for a better relaxation. This means that, the student model does not need to preserve the absolute geometry of the teacher one, while preserving global coherence through dissimilarity ranking. Our theoretical insights provide a probabilistic perspective on the process of feature representation transfer. Our experiments results show that our method outperforms or achieves on-par performance compared to strong baseline methods for representation transferring.

Convolutional Rectangular Attention Module

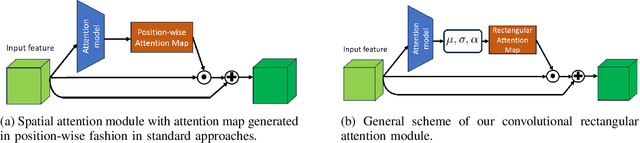
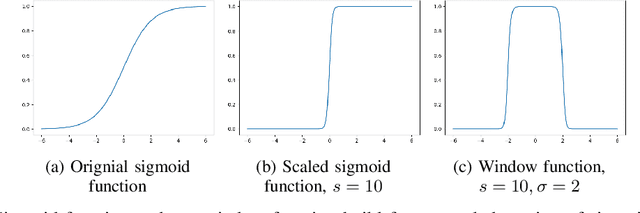
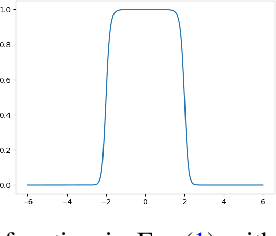
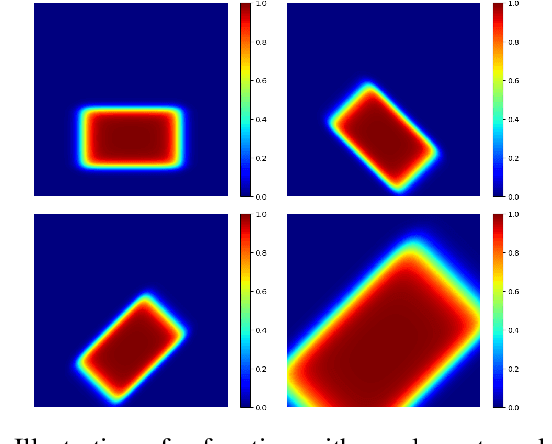
In this paper, we introduce a novel spatial attention module, that can be integrated to any convolutional network. This module guides the model to pay attention to the most discriminative part of an image. This enables the model to attain a better performance by an end-to-end training. In standard approaches, a spatial attention map is generated in a position-wise fashion. We observe that this results in very irregular boundaries. This could make it difficult to generalize to new samples. In our method, the attention region is constrained to be rectangular. This rectangle is parametrized by only 5 parameters, allowing for a better stability and generalization to new samples. In our experiments, our method systematically outperforms the position-wise counterpart. Thus, this provides us a novel useful spatial attention mechanism for convolutional models. Besides, our module also provides the interpretability concerning the ``where to look" question, as it helps to know the part of the input on which the model focuses to produce the prediction.

Large Margin Discriminative Loss for Classification

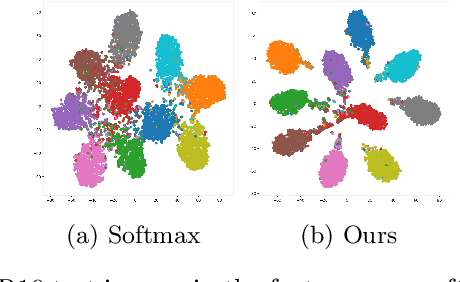
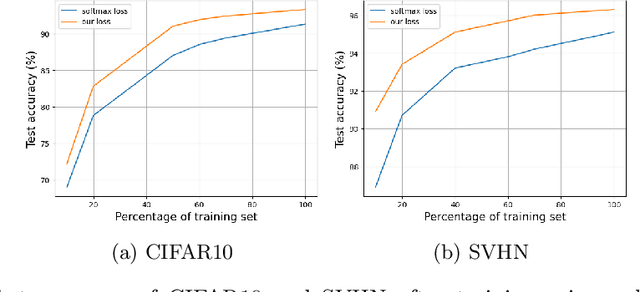
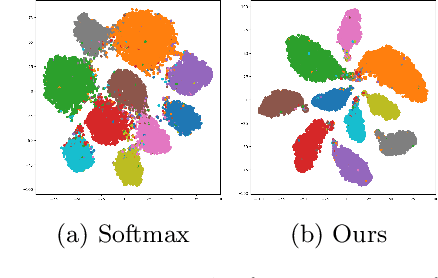
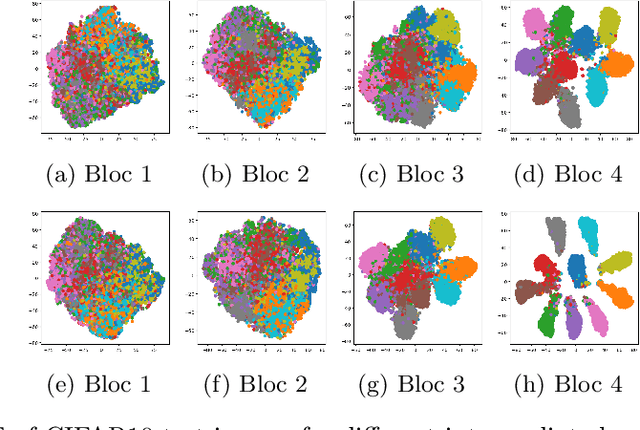
In this paper, we introduce a novel discriminative loss function with large margin in the context of Deep Learning. This loss boosts the discriminative power of neural nets, represented by intra-class compactness and inter-class separability. On the one hand, the class compactness is ensured by close distance of samples of the same class to each other. On the other hand, the inter-class separability is boosted by a margin loss that ensures the minimum distance of each class to its closest boundary. All the terms in our loss have an explicit meaning, giving a direct view of the feature space obtained. We analyze mathematically the relation between compactness and margin term, giving a guideline about the impact of the hyper-parameters on the learned features. Moreover, we also analyze properties of the gradient of the loss with respect to the parameters of the neural net. Based on this, we design a strategy called partial momentum updating that enjoys simultaneously stability and consistency in training. Furthermore, we also investigate generalization errors to have better theoretical insights. Our loss function systematically boosts the test accuracy of models compared to the standard softmax loss in our experiments.

Sensitivity Analysis for Active Sampling, with Applications to the Simulation of Analog Circuits

We propose an active sampling flow, with the use-case of simulating the impact of combined variations on analog circuits. In such a context, given the large number of parameters, it is difficult to fit a surrogate model and to efficiently explore the space of design features. By combining a drastic dimension reduction using sensitivity analysis and Bayesian surrogate modeling, we obtain a flexible active sampling flow. On synthetic and real datasets, this flow outperforms the usual Monte-Carlo sampling which often forms the foundation of design space exploration.

Statistical Edge Detection And UDF Learning For Shape Representation

In the field of computer vision, the numerical encoding of 3D surfaces is crucial. It is classical to represent surfaces with their Signed Distance Functions (SDFs) or Unsigned Distance Functions (UDFs). For tasks like representation learning, surface classification, or surface reconstruction, this function can be learned by a neural network, called Neural Distance Function. This network, and in particular its weights, may serve as a parametric and implicit representation for the surface. The network must represent the surface as accurately as possible. In this paper, we propose a method for learning UDFs that improves the fidelity of the obtained Neural UDF to the original 3D surface. The key idea of our method is to concentrate the learning effort of the Neural UDF on surface edges. More precisely, we show that sampling more training points around surface edges allows better local accuracy of the trained Neural UDF, and thus improves the global expressiveness of the Neural UDF in terms of Hausdorff distance. To detect surface edges, we propose a new statistical method based on the calculation of a $p$-value at each point on the surface. Our method is shown to detect surface edges more accurately than a commonly used local geometric descriptor.

Combining Statistical Depth and Fermat Distance for Uncertainty Quantification

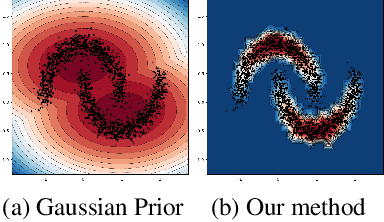
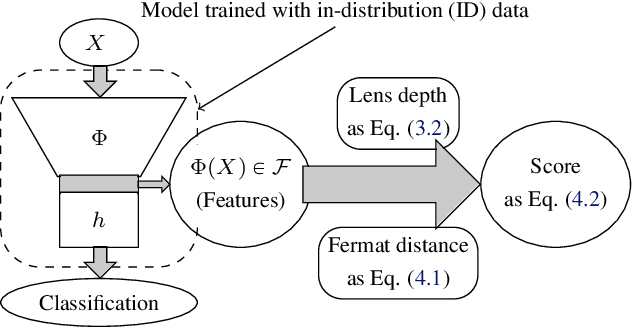
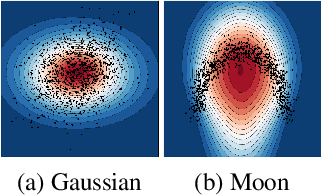
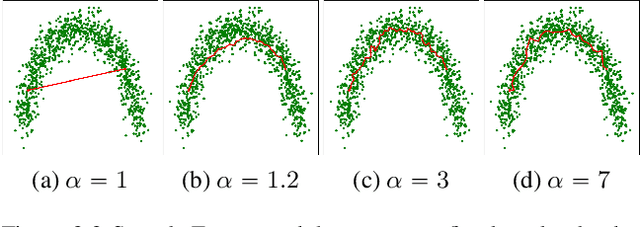
We measure the Out-of-domain uncertainty in the prediction of Neural Networks using a statistical notion called ``Lens Depth'' (LD) combined with Fermat Distance, which is able to capture precisely the ``depth'' of a point with respect to a distribution in feature space, without any assumption about the form of distribution. Our method has no trainable parameter. The method is applicable to any classification model as it is applied directly in feature space at test time and does not intervene in training process. As such, it does not impact the performance of the original model. The proposed method gives excellent qualitative result on toy datasets and can give competitive or better uncertainty estimation on standard deep learning datasets compared to strong baseline methods.

Conformal inference for regression on Riemannian Manifolds

Regression on manifolds, and, more broadly, statistics on manifolds, has garnered significant importance in recent years due to the vast number of applications for this type of data. Circular data is a classic example, but so is data in the space of covariance matrices, data on the Grassmannian manifold obtained as a result of principal component analysis, among many others. In this work we investigate prediction sets for regression scenarios when the response variable, denoted by $Y$, resides in a manifold, and the covariable, denoted by X, lies in Euclidean space. This extends the concepts delineated in [Lei and Wasserman, 2014] to this novel context. Aligning with traditional principles in conformal inference, these prediction sets are distribution-free, indicating that no specific assumptions are imposed on the joint distribution of $(X, Y)$, and they maintain a non-parametric character. We prove the asymptotic almost sure convergence of the empirical version of these regions on the manifold to their population counterparts. The efficiency of this method is shown through a comprehensive simulation study and an analysis involving real-world data.

Understanding black-box models with dependent inputs through a generalization of Hoeffding's decomposition

One of the main challenges for interpreting black-box models is the ability to uniquely decompose square-integrable functions of non-mutually independent random inputs into a sum of functions of every possible subset of variables. However, dealing with dependencies among inputs can be complicated. We propose a novel framework to study this problem, linking three domains of mathematics: probability theory, functional analysis, and combinatorics. We show that, under two reasonable assumptions on the inputs (non-perfect functional dependence and non-degenerate stochastic dependence), it is always possible to decompose uniquely such a function. This ``canonical decomposition'' is relatively intuitive and unveils the linear nature of non-linear functions of non-linearly dependent inputs. In this framework, we effectively generalize the well-known Hoeffding decomposition, which can be seen as a particular case. Oblique projections of the black-box model allow for novel interpretability indices for evaluation and variance decomposition. Aside from their intuitive nature, the properties of these novel indices are studied and discussed. This result offers a path towards a more precise uncertainty quantification, which can benefit sensitivity analyses and interpretability studies, whenever the inputs are dependent. This decomposition is illustrated analytically, and the challenges to adopting these results in practice are discussed.