Exposing the Illusion of Fairness: Auditing Vulnerabilities to Distributional Manipulation Attacks

Proving the compliance of AI algorithms has become an important challenge with the growing deployment of such algorithms for real-life applications. Inspecting possible biased behaviors is mandatory to satisfy the constraints of the regulations of the EU Artificial Intelligence's Act. Regulation-driven audits increasingly rely on global fairness metrics, with Disparate Impact being the most widely used. Yet such global measures depend highly on the distribution of the sample on which the measures are computed. We investigate first how to manipulate data samples to artificially satisfy fairness criteria, creating minimally perturbed datasets that remain statistically indistinguishable from the original distribution while satisfying prescribed fairness constraints. Then we study how to detect such manipulation. Our analysis (i) introduces mathematically sound methods for modifying empirical distributions under fairness constraints using entropic or optimal transport projections, (ii) examines how an auditee could potentially circumvent fairness inspections, and (iii) offers recommendations to help auditors detect such data manipulations. These results are validated through experiments on classical tabular datasets in bias detection.

When majority rules, minority loses: bias amplification of gradient descent

Despite growing empirical evidence of bias amplification in machine learning, its theoretical foundations remain poorly understood. We develop a formal framework for majority-minority learning tasks, showing how standard training can favor majority groups and produce stereotypical predictors that neglect minority-specific features. Assuming population and variance imbalance, our analysis reveals three key findings: (i) the close proximity between ``full-data'' and stereotypical predictors, (ii) the dominance of a region where training the entire model tends to merely learn the majority traits, and (iii) a lower bound on the additional training required. Our results are illustrated through experiments in deep learning for tabular and image classification tasks.

PLS-based approach for fair representation learning

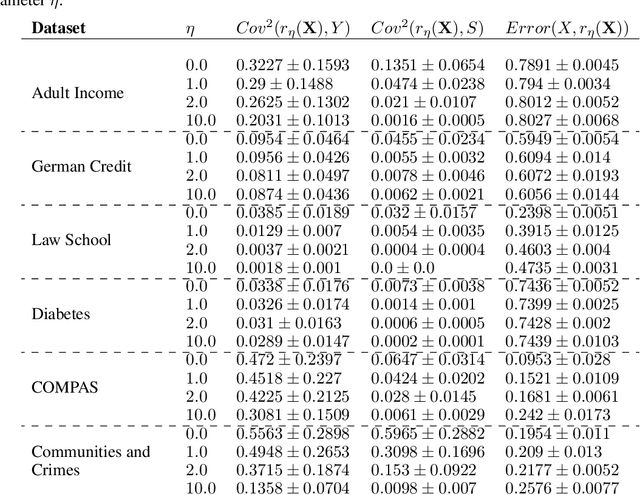
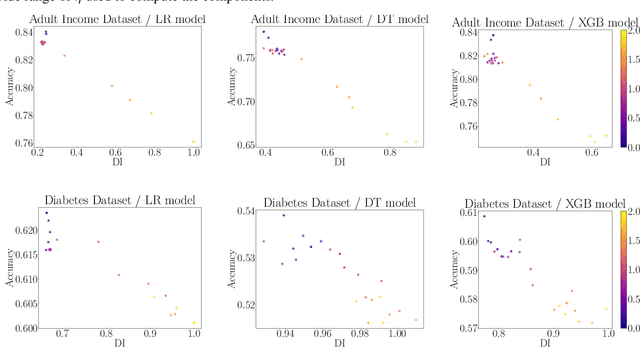
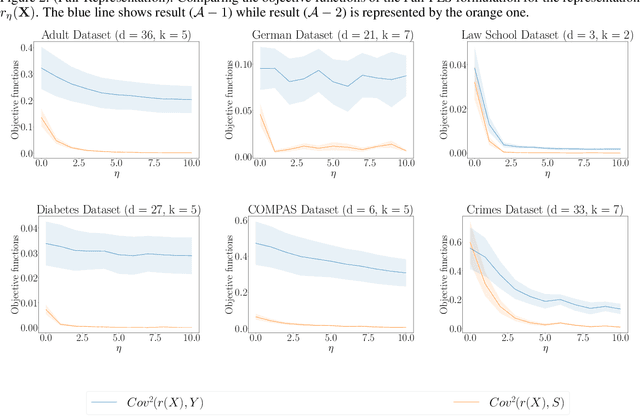
We revisit the problem of fair representation learning by proposing Fair Partial Least Squares (PLS) components. PLS is widely used in statistics to efficiently reduce the dimension of the data by providing representation tailored for the prediction. We propose a novel method to incorporate fairness constraints in the construction of PLS components. This new algorithm provides a feasible way to construct such features both in the linear and the non linear case using kernel embeddings. The efficiency of our method is evaluated on different datasets, and we prove its superiority with respect to standard fair PCA method.

Learning with Differentially Private (Sliced) Wasserstein Gradients

In this work, we introduce a novel framework for privately optimizing objectives that rely on Wasserstein distances between data-dependent empirical measures. Our main theoretical contribution is, based on an explicit formulation of the Wasserstein gradient in a fully discrete setting, a control on the sensitivity of this gradient to individual data points, allowing strong privacy guarantees at minimal utility cost. Building on these insights, we develop a deep learning approach that incorporates gradient and activations clipping, originally designed for DP training of problems with a finite-sum structure. We further demonstrate that privacy accounting methods extend to Wasserstein-based objectives, facilitating large-scale private training. Empirical results confirm that our framework effectively balances accuracy and privacy, offering a theoretically sound solution for privacy-preserving machine learning tasks relying on optimal transport distances such as Wasserstein distance or sliced-Wasserstein distance.

Fair Graph Neural Network with Supervised Contrastive Regularization

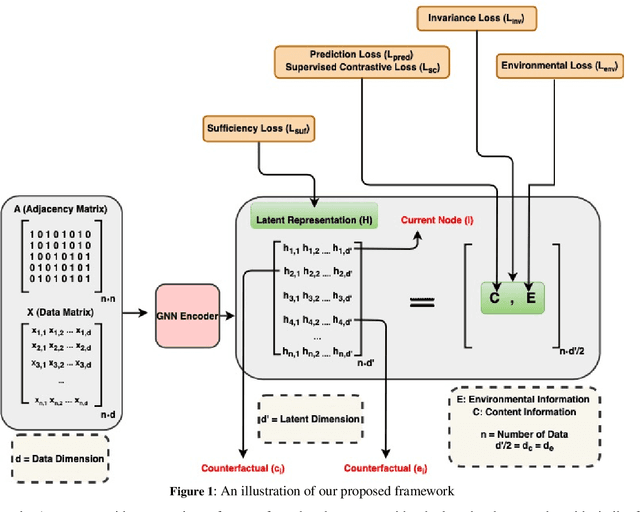
In recent years, Graph Neural Networks (GNNs) have made significant advancements, particularly in tasks such as node classification, link prediction, and graph representation. However, challenges arise from biases that can be hidden not only in the node attributes but also in the connections between entities. Therefore, ensuring fairness in graph neural network learning has become a critical problem. To address this issue, we propose a novel model for training fairness-aware GNN, which enhances the Counterfactual Augmented Fair Graph Neural Network Framework (CAF). Our approach integrates Supervised Contrastive Loss and Environmental Loss to enhance both accuracy and fairness. Experimental validation on three real datasets demonstrates the superiority of our proposed model over CAF and several other existing graph-based learning methods.

Debiasing Machine Learning Models by Using Weakly Supervised Learning

We tackle the problem of bias mitigation of algorithmic decisions in a setting where both the output of the algorithm and the sensitive variable are continuous. Most of prior work deals with discrete sensitive variables, meaning that the biases are measured for subgroups of persons defined by a label, leaving out important algorithmic bias cases, where the sensitive variable is continuous. Typical examples are unfair decisions made with respect to the age or the financial status. In our work, we then propose a bias mitigation strategy for continuous sensitive variables, based on the notion of endogeneity which comes from the field of econometrics. In addition to solve this new problem, our bias mitigation strategy is a weakly supervised learning method which requires that a small portion of the data can be measured in a fair manner. It is model agnostic, in the sense that it does not make any hypothesis on the prediction model. It also makes use of a reasonably large amount of input observations and their corresponding predictions. Only a small fraction of the true output predictions should be known. This therefore limits the need for expert interventions. Results obtained on synthetic data show the effectiveness of our approach for examples as close as possible to real-life applications in econometrics.

Understanding black-box models with dependent inputs through a generalization of Hoeffding's decomposition

One of the main challenges for interpreting black-box models is the ability to uniquely decompose square-integrable functions of non-mutually independent random inputs into a sum of functions of every possible subset of variables. However, dealing with dependencies among inputs can be complicated. We propose a novel framework to study this problem, linking three domains of mathematics: probability theory, functional analysis, and combinatorics. We show that, under two reasonable assumptions on the inputs (non-perfect functional dependence and non-degenerate stochastic dependence), it is always possible to decompose uniquely such a function. This ``canonical decomposition'' is relatively intuitive and unveils the linear nature of non-linear functions of non-linearly dependent inputs. In this framework, we effectively generalize the well-known Hoeffding decomposition, which can be seen as a particular case. Oblique projections of the black-box model allow for novel interpretability indices for evaluation and variance decomposition. Aside from their intuitive nature, the properties of these novel indices are studied and discussed. This result offers a path towards a more precise uncertainty quantification, which can benefit sensitivity analyses and interpretability studies, whenever the inputs are dependent. This decomposition is illustrated analytically, and the challenges to adopting these results in practice are discussed.

Improved learning theory for kernel distribution regression with two-stage sampling

The distribution regression problem encompasses many important statistics and machine learning tasks, and arises in a large range of applications. Among various existing approaches to tackle this problem, kernel methods have become a method of choice. Indeed, kernel distribution regression is both computationally favorable, and supported by a recent learning theory. This theory also tackles the two-stage sampling setting, where only samples from the input distributions are available. In this paper, we improve the learning theory of kernel distribution regression. We address kernels based on Hilbertian embeddings, that encompass most, if not all, of the existing approaches. We introduce the novel near-unbiased condition on the Hilbertian embeddings, that enables us to provide new error bounds on the effect of the two-stage sampling, thanks to a new analysis. We show that this near-unbiased condition holds for three important classes of kernels, based on optimal transport and mean embedding. As a consequence, we strictly improve the existing convergence rates for these kernels. Our setting and results are illustrated by numerical experiments.

Are fairness metric scores enough to assess discrimination biases in machine learning?

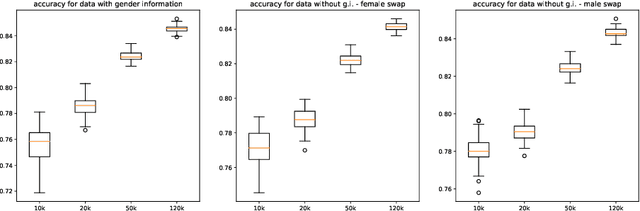
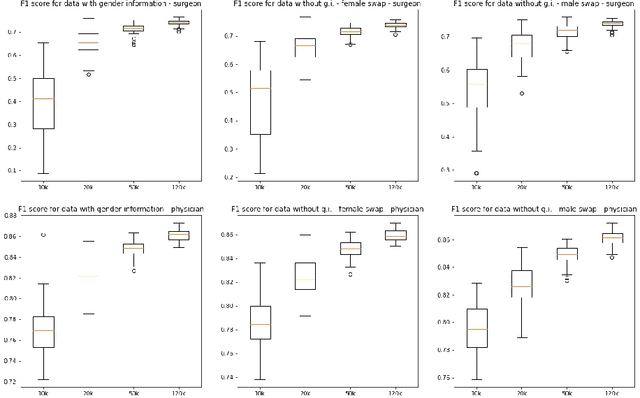
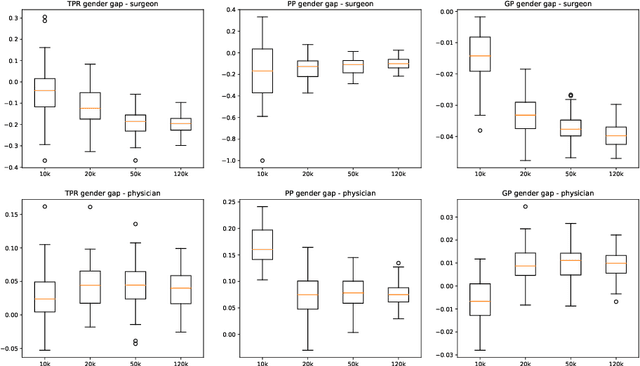
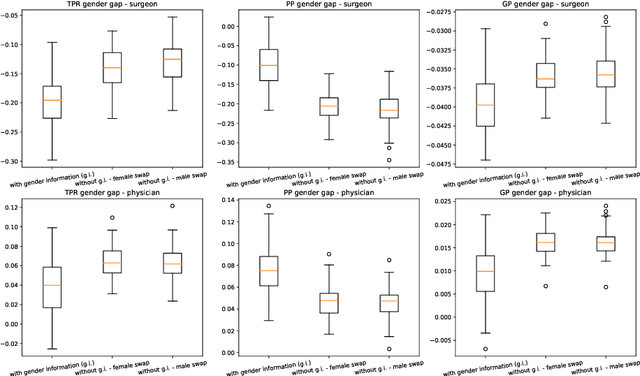
This paper presents novel experiments shedding light on the shortcomings of current metrics for assessing biases of gender discrimination made by machine learning algorithms on textual data. We focus on the Bios dataset, and our learning task is to predict the occupation of individuals, based on their biography. Such prediction tasks are common in commercial Natural Language Processing (NLP) applications such as automatic job recommendations. We address an important limitation of theoretical discussions dealing with group-wise fairness metrics: they focus on large datasets, although the norm in many industrial NLP applications is to use small to reasonably large linguistic datasets for which the main practical constraint is to get a good prediction accuracy. We then question how reliable are different popular measures of bias when the size of the training set is simply sufficient to learn reasonably accurate predictions. Our experiments sample the Bios dataset and learn more than 200 models on different sample sizes. This allows us to statistically study our results and to confirm that common gender bias indices provide diverging and sometimes unreliable results when applied to relatively small training and test samples. This highlights the crucial importance of variance calculations for providing sound results in this field.

How optimal transport can tackle gender biases in multi-class neural-network classifiers for job recommendations?

Automatic recommendation systems based on deep neural networks have become extremely popular during the last decade. Some of these systems can however be used for applications which are ranked as High Risk by the European Commission in the A.I. act, as for instance for online job candidate recommendation. When used in the European Union, commercial AI systems for this purpose will then be required to have to proper statistical properties with regard to potential discrimination they could engender. This motivated our contribution, where we present a novel optimal transport strategy to mitigate undesirable algorithmic biases in multi-class neural-network classification. Our stratey is model agnostic and can be used on any multi-class classification neural-network model. To anticipate the certification of recommendation systems using textual data, we then used it on the Bios dataset, for which the learning task consists in predicting the occupation of female and male individuals, based on their LinkedIn biography. Results show that it can reduce undesired algorithmic biases in this context to lower levels than a standard strategy.