On the nonconvexity of some push-forward constraints and its consequences in machine learning

The push-forward operation enables one to redistribute a probability measure through a deterministic map. It plays a key role in statistics and optimization: many learning problems (notably from optimal transport, generative modeling, and algorithmic fairness) include constraints or penalties framed as push-forward conditions on the model. However, the literature lacks general theoretical insights on the (non)convexity of such constraints and its consequences on the associated learning problems. This paper aims at filling this gap. In a first part, we provide a range of sufficient and necessary conditions for the (non)convexity of two sets of functions: the maps transporting one probability measure to another; the maps inducing equal output distributions across distinct probability measures. This highlights that for most probability measures, these push-forward constraints are not convex. In a second time, we show how this result implies critical limitations on the design of convex optimization problems for learning generative models or group-fair predictors. This work will hopefully help researchers and practitioners have a better understanding of the critical impact of push-forward conditions onto convexity.

Improved learning theory for kernel distribution regression with two-stage sampling

The distribution regression problem encompasses many important statistics and machine learning tasks, and arises in a large range of applications. Among various existing approaches to tackle this problem, kernel methods have become a method of choice. Indeed, kernel distribution regression is both computationally favorable, and supported by a recent learning theory. This theory also tackles the two-stage sampling setting, where only samples from the input distributions are available. In this paper, we improve the learning theory of kernel distribution regression. We address kernels based on Hilbertian embeddings, that encompass most, if not all, of the existing approaches. We introduce the novel near-unbiased condition on the Hilbertian embeddings, that enables us to provide new error bounds on the effect of the two-stage sampling, thanks to a new analysis. We show that this near-unbiased condition holds for three important classes of kernels, based on optimal transport and mean embedding. As a consequence, we strictly improve the existing convergence rates for these kernels. Our setting and results are illustrated by numerical experiments.

GAN Estimation of Lipschitz Optimal Transport Maps

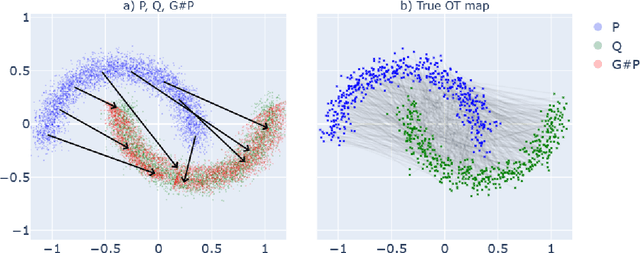
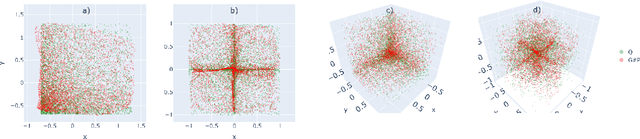
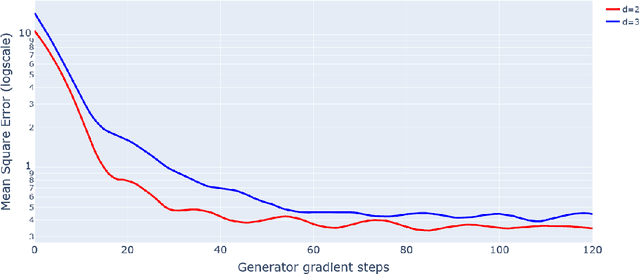
This paper introduces the first statistically consistent estimator of the optimal transport map between two probability distributions, based on neural networks. Building on theoretical and practical advances in the field of Lipschitz neural networks, we define a Lipschitz-constrained generative adversarial network penalized by the quadratic transportation cost. Then, we demonstrate that, under regularity assumptions, the obtained generator converges uniformly to the optimal transport map as the sample size increases to infinity. Furthermore, we show through a number of numerical experiments that the learnt mapping has promising performances. In contrast to previous work tackling either statistical guarantees or practicality, we provide an expressive and feasible estimator which paves way for optimal transport applications where the asymptotic behaviour must be certified.

Transport-based Counterfactual Models

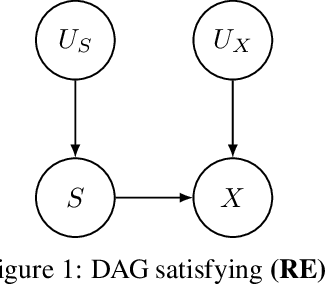
Counterfactual frameworks have grown popular in explainable and fair machine learning, as they offer a natural notion of causation. However, state-of-the-art models to compute counterfactuals are either unrealistic or unfeasible. In particular, while Pearl's causal inference provides appealing rules to calculate counterfactuals, it relies on a model that is unknown and hard to discover in practice. We address the problem of designing realistic and feasible counterfactuals in the absence of a causal model. We define transport-based counterfactual models as collections of joint probability distributions between observable distributions, and show their connection to causal counterfactuals. More specifically, we argue that optimal transport theory defines relevant transport-based counterfactual models, as they are numerically feasible, statistically-faithful, and can even coincide with causal counterfactual models. We illustrate the practicality of these models by defining sharper fairness criteria than typical group fairness conditions.

The Many Faces of 1-Lipschitz Neural Networks

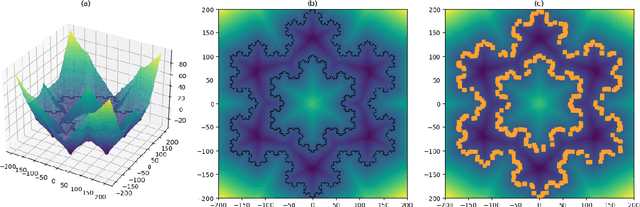
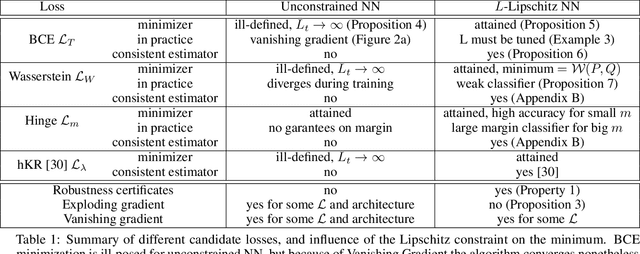
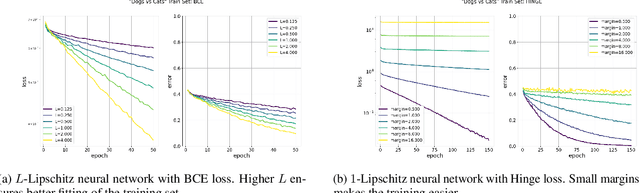
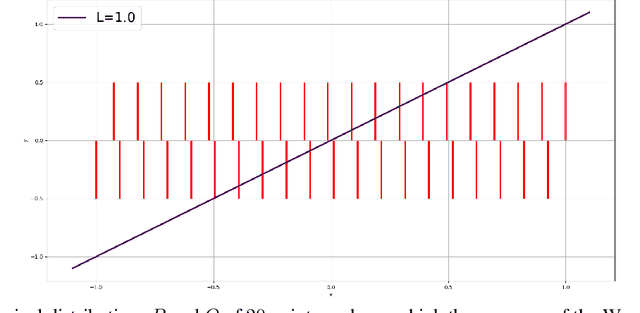
Lipschitz constrained models have been used to solve specifics deep learning problems such as the estimation of Wasserstein distance for GAN, or the training of neural networks robust to adversarial attacks. Regardless the novel and effective algorithms to build such 1-Lipschitz networks, their usage remains marginal, and they are commonly considered as less expressive and less able to fit properly the data than their unconstrained counterpart. The goal of the paper is to demonstrate that, despite being empirically harder to train, 1-Lipschitz neural networks are theoretically better grounded than unconstrained ones when it comes to classification. To achieve that we recall some results about 1-Lipschitz function in the scope of deep learning and we extend and illustrate them to derive general properties for classification. First, we show that 1-Lipschitz neural network can fit arbitrarily difficult frontier making them as expressive as classical ones. When minimizing the log loss, we prove that the optimization problem under Lipschitz constraint is well posed and have a minimum, whereas regular neural networks can diverge even on remarkably simple situations. Then, we study the link between classification with 1-Lipschitz network and optimal transport thanks to regularized versions of Kantorovich-Rubinstein duality theory. Last, we derive preliminary bounds on their VC dimension.

Achieving robustness in classification using optimal transport with hinge regularization

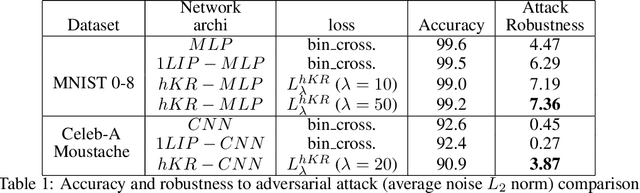
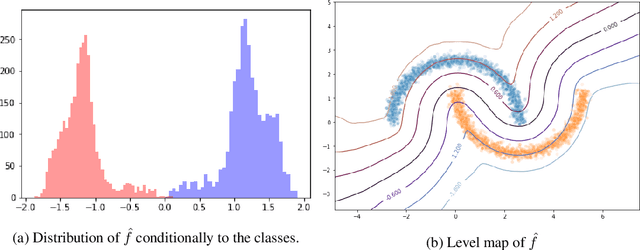
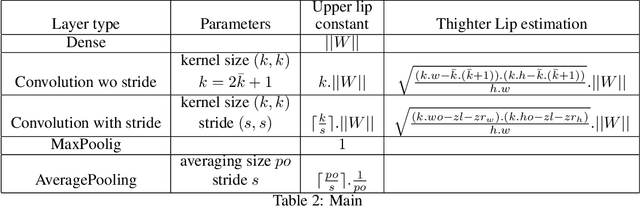
We propose a new framework for robust binary classification, with Deep Neural Networks, based on a hinge regularization of the Kantorovich-Rubinstein dual formulation for the estimation of the Wasserstein distance. The robustness of the approach is guaranteed by the strict Lipschitz constraint on functions required by the optimization problem and direct interpretation of the loss in terms of adversarial robustness. We prove that this classification formulation has a solution, and is still the dual formulation of an optimal transportation problem. We also establish the geometrical properties of this optimal solution. We summarize state-of-the-art methods to enforce Lipschitz constraints on neural networks and we propose new ones for convolutional networks (associated with an open source library for this purpose). The experiments show that the approach provides the expected guarantees in terms of robustness without any significant accuracy drop. The results also suggest that adversarial attacks on the proposed models visibly and meaningfully change the input, and can thus serve as an explanation for the classification.