On the nonconvexity of some push-forward constraints and its consequences in machine learning

The push-forward operation enables one to redistribute a probability measure through a deterministic map. It plays a key role in statistics and optimization: many learning problems (notably from optimal transport, generative modeling, and algorithmic fairness) include constraints or penalties framed as push-forward conditions on the model. However, the literature lacks general theoretical insights on the (non)convexity of such constraints and its consequences on the associated learning problems. This paper aims at filling this gap. In a first part, we provide a range of sufficient and necessary conditions for the (non)convexity of two sets of functions: the maps transporting one probability measure to another; the maps inducing equal output distributions across distinct probability measures. This highlights that for most probability measures, these push-forward constraints are not convex. In a second time, we show how this result implies critical limitations on the design of convex optimization problems for learning generative models or group-fair predictors. This work will hopefully help researchers and practitioners have a better understanding of the critical impact of push-forward conditions onto convexity.

GAN Estimation of Lipschitz Optimal Transport Maps

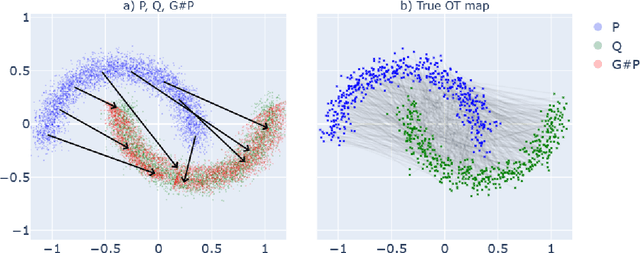
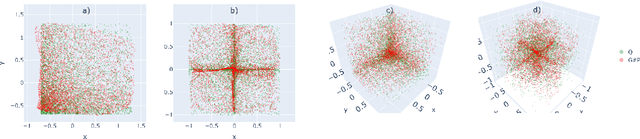
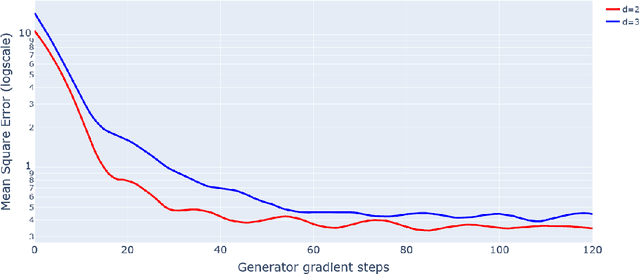
This paper introduces the first statistically consistent estimator of the optimal transport map between two probability distributions, based on neural networks. Building on theoretical and practical advances in the field of Lipschitz neural networks, we define a Lipschitz-constrained generative adversarial network penalized by the quadratic transportation cost. Then, we demonstrate that, under regularity assumptions, the obtained generator converges uniformly to the optimal transport map as the sample size increases to infinity. Furthermore, we show through a number of numerical experiments that the learnt mapping has promising performances. In contrast to previous work tackling either statistical guarantees or practicality, we provide an expressive and feasible estimator which paves way for optimal transport applications where the asymptotic behaviour must be certified.

Transport-based Counterfactual Models

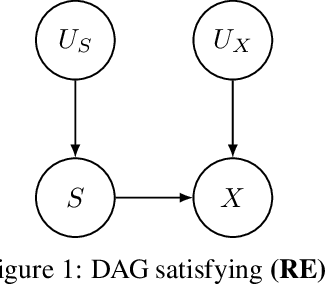
Counterfactual frameworks have grown popular in explainable and fair machine learning, as they offer a natural notion of causation. However, state-of-the-art models to compute counterfactuals are either unrealistic or unfeasible. In particular, while Pearl's causal inference provides appealing rules to calculate counterfactuals, it relies on a model that is unknown and hard to discover in practice. We address the problem of designing realistic and feasible counterfactuals in the absence of a causal model. We define transport-based counterfactual models as collections of joint probability distributions between observable distributions, and show their connection to causal counterfactuals. More specifically, we argue that optimal transport theory defines relevant transport-based counterfactual models, as they are numerically feasible, statistically-faithful, and can even coincide with causal counterfactual models. We illustrate the practicality of these models by defining sharper fairness criteria than typical group fairness conditions.