GAN Estimation of Lipschitz Optimal Transport Maps
Paper and Code
Feb 16, 2022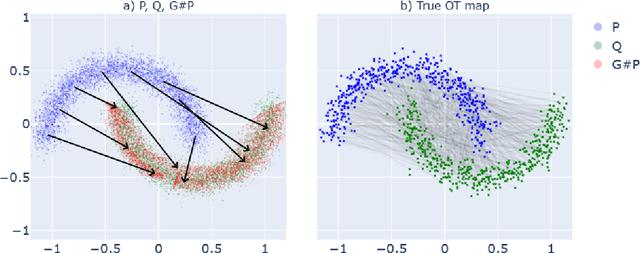
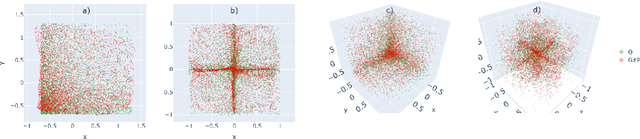
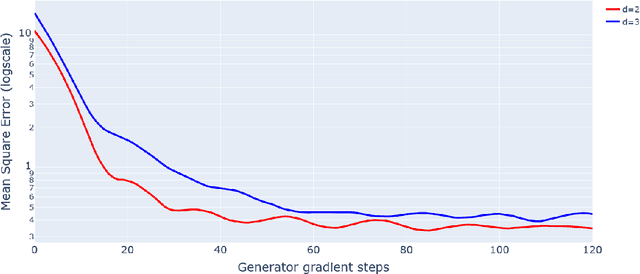
This paper introduces the first statistically consistent estimator of the optimal transport map between two probability distributions, based on neural networks. Building on theoretical and practical advances in the field of Lipschitz neural networks, we define a Lipschitz-constrained generative adversarial network penalized by the quadratic transportation cost. Then, we demonstrate that, under regularity assumptions, the obtained generator converges uniformly to the optimal transport map as the sample size increases to infinity. Furthermore, we show through a number of numerical experiments that the learnt mapping has promising performances. In contrast to previous work tackling either statistical guarantees or practicality, we provide an expressive and feasible estimator which paves way for optimal transport applications where the asymptotic behaviour must be certified.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge